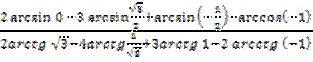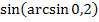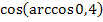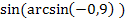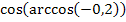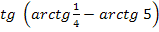Методические указания
К практическим занятиям
по дисциплине
Математическая составляющая естественно-научных дисциплин
Направление подготовки: 01.03.02 «Прикладная математика и информатика»
Профиль подготовки: «Прикладная математика и информатика»
Форма обучения:очная
Тула 2016 г.
Методические указания к практическим занятиям составлены доцентом каф. ПМиИ Ю.В. Московскойи обсуждены на заседании кафедры Прикладной математики и информатики Механико-математического факультета
протокол № 10 от " 16 " мая 2016 г.
Зав. кафедрой________________В.И. Иванов
Методические указания к практическим (семинарским) занятиям пересмотрены и утверждены на заседании кафедры Прикладной математики и информатики Механико-математического факультета
протокол №___ от "___"____________ 20___ г.
Зав. кафедрой________________В.И. Иванов
Цели и задачи практических занятий
Целями практических занятий по дисциплине «Математическая составляющая естественно-научных дисциплин»являются формирование математической культуры студентов, фундаментальная подготовка студентов в области элементарной математики и знакомство с элементами высшей математики, овладение основным аппаратом математики для дальнейшего использования при изучении дисциплин естественнонаучного содержания и в других областях математического знания.
Задачами освоения дисциплины являются:
- фундаментальная подготовка студентов в области элементарной математики и знакомство с элементами высшей математики,
- подготовка студентов к усвоению материала при изучении специальных математических дисциплин,
- приобретение практических навыков решения математических задач.
Методические указания к проведению практических занятий
Занятие 1.
Тема занятия: «Множества. Числовые множества. Элементы теории множеств.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Способы задания множеств:
1) перечислением.
2) указанием характеристического свойства, т.е. такого свойства, что элементы множества им обладают, а все остальное на свете не обладает.
Диаграммы Венна.
Равенство множеств: A=B: "x xÎAÛxÎB.
Пустое множество: множество, не имеющее ни одного элемента, обозначают Æ.
Универсальное множество. Обычно все множества, с которыми имеют дело в том или ином рассуждении, являются подмножествами некоторого фиксированного множества I. Мы будем называть в этом случае множество I универсальным множеством.
Подмножество. Множество B является подмножеством другого множества A, если каждый элемент x из B является вместе с тем и элементом множества A. обозначают BÌA.
Числовые множества. Примерами таких множеств могут служить:
а) множество всех натуральных чисел,
б) множество всех целых чисел (положительных, отрицательных и нуля),
в) множество всех рациональных чисел,
г) множество всех действительных чисел.
Пересечение множеств. Множество, состоящее из общих элементов множеств A, B, называется пересечением этих множеств или их произведением. Пересечение двух множеств A и B обозначается AB или AÇB. Решение систем уравнений и неравенств, по сути дела, сводится к отысканию пересечения некоторых множеств.
Объединение (сложение) множеств. Суммой множеств A, B называют новое множество, состоящее из тех и только тех элементов, которые входят хоть в одно из слагаемых множеств (в объединении повторяющиеся элементы считаются лишь по одному разу). Сумму множеств A и B обычно обозначают A+B или AÈB.
Вычитание множеств. Разностью двух множеств A и B называют новое множество, обозначаемое A−B или A\B, в которое входят все элементы множества A, не принадлежащие B. Вычитание B из A сводится к удалению из A общей части A и B: A−B=A−AB.
Дополнение множества. Если все множества рассматриваются как подмножества универсального множества I, то обычно под дополнением множества B понимают его дополнение в I. В этом случае вместо B'_I пишут просто B'.
Задания.
1 (уст). Из примеров множеств укажите, которые заданы перечислением или их можно так задать. Приведите свои примеры. ({понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}, множество арифметических действий, множество корней квадратного уравнения x^2−2x−24=0 {−4, 6})
2 (уст). Из выше приведенных примеров множеств укажите, которые заданы характеристическим свойством. Приведите свои примеры.
3. Установите связь между числовыми множествами.
4. Что является решением уравнения (x^2 +y^2 −37)(y −x−7)=0? Ответ: множество, состоящее из окружности и прямой.
5.Данная задача, связанная с подсчетом численности конечных множеств, принадлежит известному детскому писателю Льюису Кэрроллу, автору.Алисы в стране чудес. Под псевдонимом Льюис Кэрролл писал математик Доджсон. В одной из повестей Кэрролла есть следующая задача:
В ожесточенном бою 70 из 100 пиратов потеряли один глаз, 75 — одно ухо, 80 — одну руку и 85 — одну ногу. Каково минимальное число потерявших одновременно глаз, ухо, руку и ногу?
Решение. Обозначим через A множество одноглазых, через B — множество одноухих, через C — множество одноруких и через D — множество одноногих. В задаче требуется оценить численность множества ABCD. Ясно, что все универсальное множество I можно представить как сумму этого множества ABCD и множества пиратов, сохранивших либо оба глаза, либо оба уха, либо обе руки, либо обе ноги. Поэтому I =A' +B' +C' +D' +ABCD. Отсюда следует, что численность множества I не больше суммы численностей множеств A', B', C', D' и ABCD (она была бы равна этой сумме, если бы множества A', B', C' и D' попарно не пересекались). Но численность множества A' равна 30, множества B' — 25, множества C' — 20 и множества D' — 15. Так как численность'универсального множества равна 100, то имеем 100<=30+25+20 +15+N(ABCD). Отсюда
N(ABCD)>=100−30−25−20−15=10.
Итак, не менее 10 пиратов лишились и глаза, и уха, и руки, и ноги.
6. Множество A состоит из целых чисел, делящихся на 4, множество B — из целых чисел, делящихся на 10, и множество C из целых чисел, делящихся на 75. Из каких чисел состоит множество ABC?
7. В библиотеке есть книги по разным отделам науки и искусства. Обозначим множество всех книг в библиотеке через A, а множество всех математических книг (не только в данной библиотеке) — через B. Охарактеризуйте множество A — B.
8. Множество A состоит из точек M(x; y) плоскости, для которых |x|64, |y|64, множество B — из точек плоскости, для которых x2 +y2 625, и множество C — из точек плоскости, для которых x>0. Изобразите множество AB −C.
Занятие 2.
Тема занятия: «Множества. Числовые множества. Элементы теории множеств.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Алгебра множеств.
Мы познакомились с основными действиями над множествами — сложением, вычитанием и умножением (пересечением) множеств. Эти действия обладают целым рядом свойств, напоминающих свойства действий над числами.
Роль нуля и единицы в действиях над множествами играют множества Æ (пустое множество) и I (универсальное множество).
Приведем список свойств действий над множествами:
1) AÌA.
2) Если AÌB и BÌA, то A=B.
3) Если AÌB и B ÌC, то AÌC.
4) ÆÌA.
5) AÌI.
6) A+B =B +A.
7) AB =BA.
8) A+(B +C)= (A+B)+ C.
9) A(BC)= (AB)C.
10) A+A=A.
11) AA=A.
12) A(B +C)=AB +AC.
13) A+BC =(A+B)(A+C).
14) A+Æ=A.
15) AI =A.
16) A+I =I.
17) AÆ=Æ.
18) Соотношение AÌB эквивалентно каждому из соотношений A+B =B, AB =A.
19) A+A'=I.
20) AA'=Æ.
21) Æ'=I.
22) I' =Æ.
23) (A')'=A.
24) Соотношение AÌB эквивалентно B'ÌA'.
25) (A+B)' =A'B'.
26) (AB)0 =A' +B'.
Отметим следующее замечательное.соотношение двойственности. Если в каждом из свойств 1)–26) заменить друг на друга символы Ì и É, Æ и I, È и Ç, то в результате получится снова одно из этих свойств.
Задания.
1. Упростить далее выражение (A+B)^2 =A^2 +B^2 +2AB. Ответ: A+B.
2. Доказать распределительный закон для множеств A+BC =(A+B)(A+C).
3. Доказать A+(B−C)НЕ=(A+B)−C для случая A=B=C.
Решение. A+B =A и потому (A+B)−C=A−A=Æ — пустое множество, а A+(B−C)=A+Æ=A
4. Доказать следующие формулы: (A+B)' =A'B' и (AB)' =A' +B' (на диаграмме).
5. Пользуясь правилами алгебры множеств, упростите выражение (A+B+C)(A+B)−[A+(B−C)]A.
6. Докажите равенства
а) (A−B)−C =(A−C)−(B −C);
б) (A−B)+(B −C)+ (C −A)+ ABC =A+B +C.
7. Докажите включение мноржеств AC +BD _(A+B)(C +D);
8. Вытекает ли из A−B =C, что A=B +C?
9. Вытекает ли из A=B +C, что A−B =C?
10. Какие включения справедливы для множеств A−(B +C) и (A−B)−C?
11.Упростите выражение [(X−Y)’(X’ +Y’)]’.
Занятие 3.
Тема занятия: «Делимость многочленов, деление с остатком. Симметрические многочлены и основная теорема. Неприводимые многочлены. Многоугольник Ньютона и критерий Дарбу о неприводимости. Наибольший общий делитель двух многочленов. Алгоритм Евклида.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Многочлен n-ной степени от неизвестного х:

Для сокращенной записи многочленов употребляются символы f(x), g(x) и так далее.
Умножение многочленов.
Чтобы умножить многочлен на одночлен, нужно умножить каждый член многочлена на этот одночлен и сложить полученные произведения.
(-5a)(4-b-a2)=-20a+5ab+5a3;
(2+b)(b2-4)=2b2-8+b3-4b.
Деление многочленов.
Многочлен 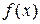 делится на многочлен
делится на многочлен 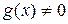 , если существует такой многочлен
, если существует такой многочлен 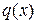 , что выполняется равенство
, что выполняется равенство 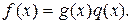
Например, из равенства 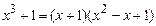 следует, что
следует, что 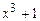 делится на многочлен
делится на многочлен 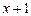 и на многочлен
и на многочлен 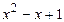 .
.
Многочлен 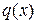 в равенстве называется частным от деления
в равенстве называется частным от деления 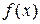 на
на 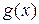 , а
, а 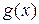 – делителем.
– делителем.
Основные свойства делимости многочленов:
1. Если 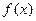 делится
делится 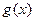 , а
, а 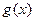 делится на
делится на 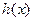 , то
, то 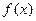 будет делиться на
будет делиться на 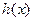 .
.
2. Если 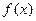 и
и 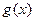 делятся на
делятся на 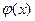 , то их сумма и разность также делятся на
, то их сумма и разность также делятся на 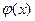 .
.
3. Если 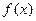 делится на
делится на 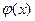 , то произведение
, то произведение 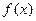 на любой многочлен
на любой многочлен 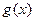 также будет делиться на
также будет делиться на 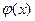 .
.
4. Если каждый из многочленов 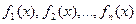 делится на
делится на 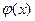 , то на
, то на 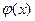 будет делиться и многочлен
будет делиться и многочлен 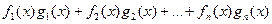 , где
, где 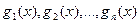 - произвольные многочлены.
- произвольные многочлены.
5. Всякий многочлен 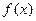 делится на любой многочлен нулевой степени.
делится на любой многочлен нулевой степени.
6. Если 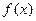 делится на
делится на 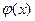 , то
, то 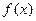 делится и на с*
делится и на с* 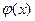 , где с – произвольное число отличное от нуля.
, где с – произвольное число отличное от нуля.
7. Многочлены 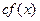 ,
, 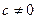 , и только они будут делителями многочлена
, и только они будут делителями многочлена 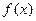 , имеющими такую же степень, что и
, имеющими такую же степень, что и 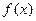 .
.
8. Тогда и только тогда многочлены 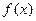 ,
, 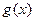 одновременно делятся друг на друга, если
одновременно делятся друг на друга, если 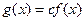 ,
, 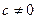 .
.
9. Всякий делитель одного из двух многочленов 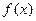 ,
, 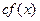 , где
, где 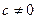 , будет делителем и для другого многочлена.
, будет делителем и для другого многочлена.
Неприводимый многочлен.
Неприводимый многочлен - это многочлен, не разлагающийся на множители более низкой степени.
Задания.
№ 1. Для каких целых чисел n число 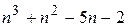 является простым.
является простым.
Решение.
Натуральное число, отличное от 1, называется простым, если оно делится только на 1 и на само себя; целое отрицательное число k называется простым, если число –k простое.
Для ответа на поставленный вопрос заметим, что справедливо равенство
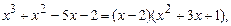
и поэтому число 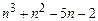 делится на
делится на 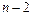 и на
и на 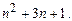 Следовательно, оно может быть простым только в случае, когда один из этих делителей равен 1 или –1, т.е. выполняется хотя бы одно из равенств
Следовательно, оно может быть простым только в случае, когда один из этих делителей равен 1 или –1, т.е. выполняется хотя бы одно из равенств 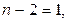
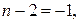
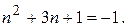
Остается проверить следующие значения n: 3, 1, 0, -3, -1 и –2. При этих значениях n рассматриваемое число равно соответственно 19, -5, 3, 4, так что искомое множество чисел есть 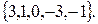
№ 2. Найти частный и остаток от деления 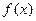 на
на 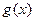 .
.
1. 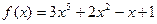 и
и 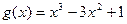
Решение.
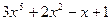 |
| 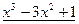
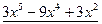
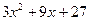
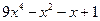
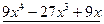
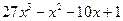
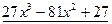

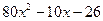
Частным от деления 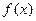 на
на 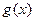 является многочлен
является многочлен 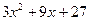 , остатком –
, остатком – 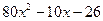 .
.
2. 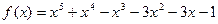 и
и 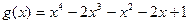
№ 3. Найти наибольший общий делитель многочленов 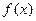 и
и 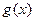 .
.
1. 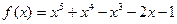 и
и 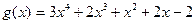
2. 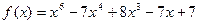 и
и 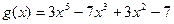
Разделить многочлен f(x) на многочлен g(x):
1. 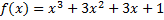 ,
, 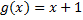 ;
;
2. 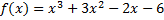 ,
, 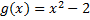 ;
;
3. 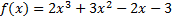 ,
, 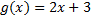 ;
;
Занятие 4.
Тема занятия: «Рациональные уравнения. Корни многочленов. Теорема Безу. Схема Горнера. Кратность корня и производная.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Корни многочленов.
Корни многочлена

есть корни рационального уравнения
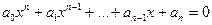
Рациональные уравнения.
Уравнение вида P(x) = 0, где P(x) - рациональная функция, называется рациональным уравнением. Часто рациональное уравнение записывают в виде равенства двух рациональных функций
f(x) = g(x)
Число a называется корнем уравнения f(x) = g(x), если при подстановке его вместо x в уравнение получается верное числовое равенство f(a) = g(a).
Можно выделить следующие методы решения рациональных уравнений:
1. Решение с помощью подстановки, т.е. введением новой переменной. Например, в уравнении aP2(x) + bP(x) + c = 0, где P(x) - многочлен, введем новую переменную y = P(x). Решаем квадратное уравнение ay2 + by + c = 0 относительно y и возвращаемся к решению уравнений P(x) = yi, где yi - решения соответствующего квадратного уравнения.
2. Решение разложением на множители. Если уравнение можно представить в виде P(x)Q(x)=0, где P(x) и Q(x) - рациональные функции, то нужно представить уравнение P(x)Q(x) = 0 в виде совокупности:
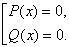
3. Однородное уравнение второго порядка aP2(x) + bP(x)Q(x) + cQ2 (x) = 0. Здесь возможны два случая. Первый - Q(x) = 0, тогда уравнение сводится к решению уравнения P(x) = 0. Второй случай - Q(x) ≠ 0, тогда исходное уравнение можно поделить на Q2 (x) и получить a(P(x)/Q(x)) 2 + bP(x)/Q(x) + c = 0. Вводим замену P(x)/Q(x) = t и получаем квадратное уравнение at2 + bt + c = 0. В ответ включаем решения обоих случаев.
4. Симметричное уравнение третьего порядка: ax3 + bx2 + bx + a = 0. Для его решения проведем следующие преобразования: ax3 + bx2 + bx + a = a(x3 + 1) + bx(x + 1) = a(x + 1)(x2- x + 1) + bx(x + 1) = (x + 1)(ax2 + (b - a)x + a). Решаем совокупность:
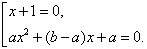
5. Симметрическое уравнение четвертого порядка ax4 + bx3 + сx2 + bx + a = 0. Сгруппируем слагаемые и разделим обе части на x2. Получим a(x2 +1/x2)+ b(x + 1/x) с = 0. Сделаем подстановку x + 1/x = t, тогда x2 + 1/x2 = t2 - 2. Получаем квадратное уравнение at2 + bt + (c - 2a) = 0. После его решения возвращаемся к исходной переменной x.
6. Возвратное уравнение. Уравнение вида ax4 + bx3 + сx2 + dx + e = 0, где a ≠ 0, b ≠ 0 иe/a = (d/b)2, называется возвратным уравнением четвертого порядка. Для его решения делим уравнение на x2 и вводим переменную t = bx + d/x, после чего получаем квадратное уравнение at2/b2 + t + с - 2ad/b = 0. Решив его, возвращаемся к исходной переменной.
7. Уравнения вида (x + a)(x + b)(x + c)(x + d) = m, где a + b = c + d. В даном случае вводим новую переменную t = x2 + (a + b)x и получаем квадратное уравнение (t + ab)(t +cd) = m. Решив его, возвращаемся к исходной переменной.
8. Уравнение вида P(x)/Q(x) = 0. Решаем уравнение P(x) = 0. Проверяем, чему равно значение Q(xi), где xi - корни уравнения P(x) = 0. Если Q(xi) ≠ 0, значит они являются решением исходного уравнения. Если Q(xi) = 0 - корень выпадает из области определения исходного уравнения и его нужно исключить из ответа.
9. Уравнение вида aP(x)/Q(x) + bQ(x)/P(x) + c = 0. Вводим новую переменную t =P(x)/Q(x) и получаем следующее уравнение: at + b/t + c = 0. Или после домножения на t (t ≠ 0) получаем квадратное уравнение at2 + ct + b = 0. Решив его, возвращаемся к исходной переменной.
10. Уравнение состоящее из суммы дробей. Один из методов состоит в том, что нужно перенести все члены уравнения в одну часть и свести уравнение к виду P(x)/Q(x) = 0.
Теорема Безу. Многочлен f(x) делится на x-c тогда и только тогда, когда число c является его корнем.
Кратность корня.
Если c – корень многочлена f(x), может оказаться, что многочлен f(x) делится не только на первую степень линейного двучлена x-c, но и на более высокие его степени. Во всяком случае, найдется такое натуральное число k, что f(x) нацело делится на 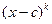 , но не делится на
, но не делится на 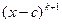 . Поэтому
. Поэтому
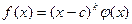 ,
,
где многочлен 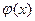 на x-c уже не делится. Число k называется кратностью корня c в многочлене f(x), а сам корень c – k- кратным корнем этого многочлена. Если k =1, то говорят, что корень с – простой.
на x-c уже не делится. Число k называется кратностью корня c в многочлене f(x), а сам корень c – k- кратным корнем этого многочлена. Если k =1, то говорят, что корень с – простой.
Производная от многочлена.
Понятие кратного корня тесно связано с понятием производной от многочлена. Пусть дан многочлен n–ной степени
f(x)= 
Его производной (первой производной) называется многочлен (n- 1)-й степени
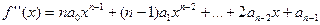
Производная от многочлена нулевой степени и от нуля считается равной нулю.
Для производной k- го порядка справедливо 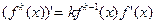
Свойства.
Многочлен 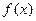 тогда и только тогда не содержит кратных множителей, если он взаимно прост со своей производной.
тогда и только тогда не содержит кратных множителей, если он взаимно прост со своей производной.
Схема Горнера.
Схема Горнера предназначена для вычисления значения полинома в точке. Пусть дан полином
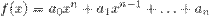
Разделим 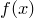 на
на 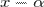 с остатком:
с остатком:
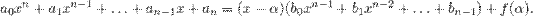
Приравняем коэффициенты при одинаковых степенях 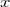 в левой и правой части:
в левой и правой части:
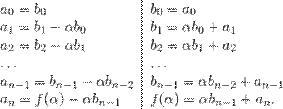
Это можно записать в виде таблицы:
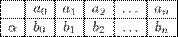
Задания.
№ 1. Решить уравнения, опираясь на теорему Безу.
1. 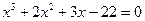
Решение.
Многочлен f(x)= 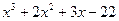 имеет корень 2. По теореме Безу f(x) делится на x-2, то есть имеет место равенство
имеет корень 2. По теореме Безу f(x) делится на x-2, то есть имеет место равенство
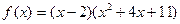 .
.
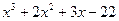 |
| 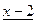
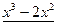
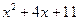
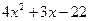
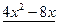
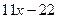
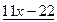
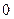
Остается решить квадратное уравнение 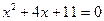 . Это уравнение не имеет действительных корней, так что x=2 – единственный действительный корень исходного уравнения.
. Это уравнение не имеет действительных корней, так что x=2 – единственный действительный корень исходного уравнения.
2. 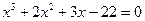
№ 2. Найти производную  многочлена
многочлена 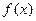 .
.
1. 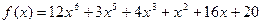
2. 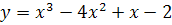
3. 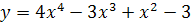
№ 3. Вычислить значение многочлена в точке, используя схему Горнера.
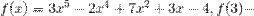
Занятие 5.
Тема занятия: «Рациональные дроби и их разложение на простейшие дроби. Рациональные неравенства.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Рациональную дробь вида Pn(x)/Qm(x), где Pn(x), Qm(x) - многочлены порядка n и m соответственно (n<m) можно разложить на элементарные дроби. Алгоритм следующий:
1. Знаменатель Qm(x) разложить на множители вида (x-x0)k, (x2+bx+c) и константу а, где (x-x0)k - множитель соответствующий корню x0 кратности k, (x2+bx+c) - множитель соответствующий случаю двух сопряженных комплексных корней, а=am - коэффициент стоящий при xm многочлена Qm(x).
2. Записать рациональную дробь вида Pn(x)/Qm(x) в виде суммы простейших дробей, у которых неизвестны коэффициенты числителя. Скобкам знаменателя вида (x-x0) соответствует дробь A/((x-x0), скобкам вида (x-x0)k соответствует сумма дробей
В1/(x-x0)+B2/(x-x0)k+...+Bk/(x-x0)k, скобкам вида (x2+bx+c) соответствует дробь
(Cx+D)/(x2+bx+c).
3. Приравниваем исходной дроби Pn(x)/Qm(x) к построенной сумме дробей находят неизвестные коэффициенты в разложении.
Задания.
№ 1. Найти числа a, b, c, при которых следующее равенство справедливо на области допустимых значений этого равенства:
-
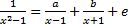 ;
; -
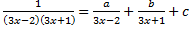 ;
;
№ 2. Разложить рациональную дробь на элементарные дроби.
- (x-1)/(x+1)
- (x^2+3x-3)/(x^3-1)
- x/(x^2-1)
- (x^2+1)/(x^2-1)
- 1/((x+1)^3+1)
Занятие 6.
Тема занятия: «Функция одной переменной. Основные понятия и определения. Элементарные функции и их графики. Преобразования функций.»
План занятия.
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Элементарные функции.
На рисунках 2 — 7 изображены графики основных элементарных функций.
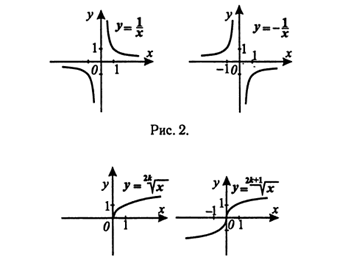
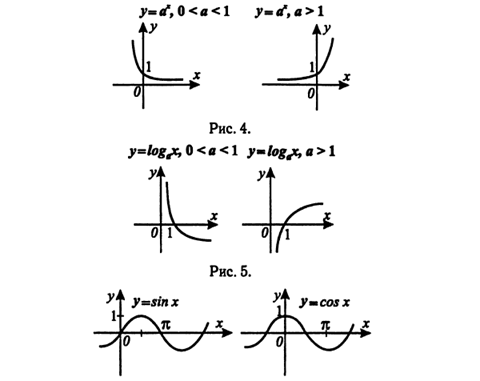
Преобразования функций.
Построение графиков функций «механическими» преобразованиями изображено на нижеследующих рисунках.
График функции у = —f(х) получен из графика функции у = f(х) отражением относительно оси Ох (см. рис. 8). График функции у = f(-х) получен из графика функции у=f(х) отражением относительно оси Оу (см. рис. 9).
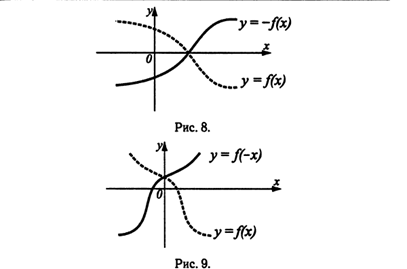
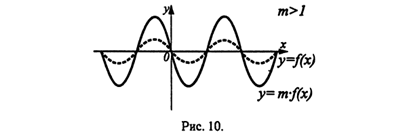
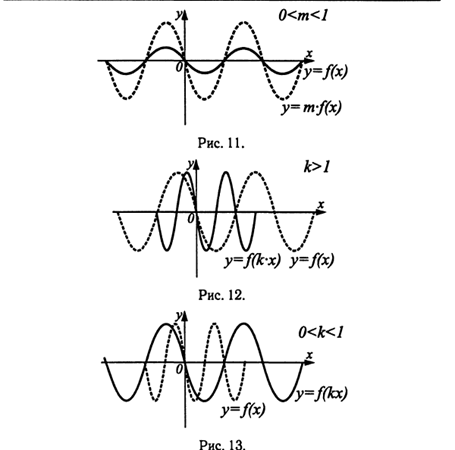
График функции у = m*f(х), m>1, получен из графика функции у = f(x) растяжением в m раз вдоль оси Оу от оси Ох (см. рис. 10). График функции у = m*f(х), 0<m<1, получен из графика функции у = f(x) сжатием в 1/m раз вдоль оси Оу к оси Ох (см. рис. 11).
График функции у = f(kx), k>1, получен из графика функции у = f(х) сжатием в к раз к оси Оу вдоль оси Ох, см. рис. 12. График функции у = f(kx), 0<k<1, получен из графика функции у = f(x) растяжением в 1/k раз от оси Оу вдоль оси Ох, см. рис. 13.
График функции у = f(x) + B получен из графика функции у =f(х) сдвигом вверх на число B при B> 0 и сдвигом вниз на число (-B) при B< О, см. рис. 14. График функции у=f(x+а) получен из графика функции у =f(x) сдвигом вправо на число -а при а < 0 и сдвигом влево на число а при а > 0, см. рис. 15.
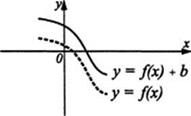
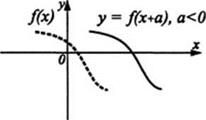
График функции у = |f(x)| (рис. 17) получен из графика функции у = f(x) (рис. 16) отражением относительно оси Ох части этого графика, лежащей ниже оси Ох. График функции у = f(|х|) (рис. 18) получен из графика функции у = f(x) (рис. 16) объединением части этого графика, лежащей правее оси Оу, с её отражением относительно оси Оу и удалением части, лежащей левее оси Оу.
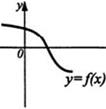
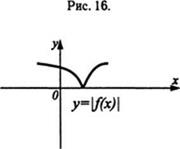
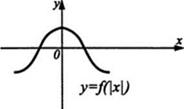
рис. 16 рис. 17. рис. 18
Задания.
Построить графики функций преобразованием от элементарных функций
-

-
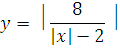
-
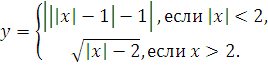
-
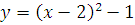
-
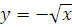
-
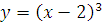
-
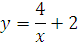
-
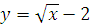
-
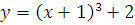
-

-
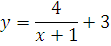
-
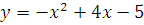
-
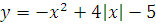
-
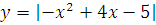
-
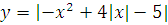
-
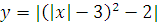
-
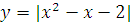
-
-
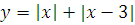
-
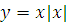
-
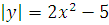
-
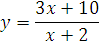
-
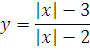
-
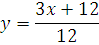
-
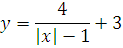
-
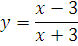
-
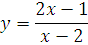
-
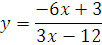
-
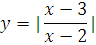
-
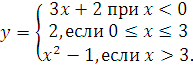
-

Занятие 7.
Тема занятия: «Обратная функция. Контрольная работа № 1.»
План занятия.
- Знакомство с теоретическим материалом. Разбор заданий под руководством преподавателя.
- Контрольная работа № 1
Методические материалы.
Функция у = f (х) называется обратимой, если она принимает каждое свое значение один раз.
Пусть f — отображение множества Е на множество М. Если для любого элемента y из множества М существует единственный элемент x — g(y) множества E, для которого F(х) = у, то отображение f называется обратимым. Отображение, обратное к у, обозначают 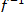 и называют обратной функцией. Функция у = f (х) при этом называется прямой функцией.
и называют обратной функцией. Функция у = f (х) при этом называется прямой функцией.
Областью определения обратной функции является множество значений функции, а множество значений является областью определения функции f.
Функции у = f (х) и х — 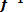 (у) называются взаимно обратными.
(у) называются взаимно обратными.
Для того чтобы некоторая функция имела обратную, необходимо и достаточно, чтобы разным значениям аргумента из области ее определения соответствовали разные значения функции
Контрольная работа № 1
Содержит задачи из разделов: "Множества. Числовые множества. Элементы теории множеств", "Делимость многочленов", "Рациональные уравнения. Корни многочленов", "Рациональные неравенства", "Элементарные функции и их графики", "Преобразования функций", "Обратная функция".
Задания.
№ 1. Задать формулой функцию, обратную данной, указать ее ООФ и МЗФ. Построить их графики:
1. f(x) = 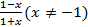
2. 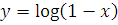
3. 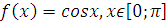
Занятие 8.
Тема занятия: «Основные тригонометрические функции и обратные тригонометрические функции.»
План занятия.
- Разбор заданий контрольной работы № 1, вызвавших наибольшую трудность
- Знакомство с теоретическим материалом.
- Разбор заданий под руководством преподавателя.
- Самостоятельное выполнение заданий.
Методические материалы.
Тригонометри́ческие фу́нкции
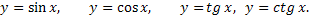
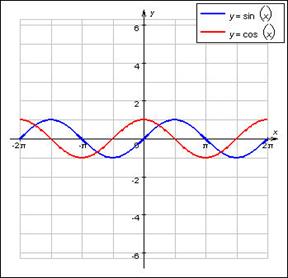
Функция y=sinx. Область определения функции: [-∞,+∞]. Область значения функции [-1,1]. Функция нечетная, периодическая с периодом 2π. Точки пересечения с осью абсцисс: x=nπ (nϵZ), эти точки являются и точками перегиба графика кривой. Функция на [ 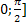 возрастает от 0 до 1 на
возрастает от 0 до 1 на 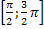 убывает от 1 до -1, на
убывает от 1 до -1, на 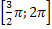 возрастает от -1 до 0. Функция на [
возрастает от -1 до 0. Функция на [ 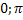 ] выпуклая, а на [
] выпуклая, а на [ 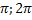 ] вогнутая.
] вогнутая.
Функция y=cosx. Область определения функции: [-∞,+∞]. Область значения функции [-1,1]. Функция четная, периодическая с периодом 2π. Точки пересечения с осью абсцисс: x= 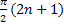 (nϵZ), эти точки являются и точками перегиба графика кривой. Функция на [
(nϵZ), эти точки являются и точками перегиба графика кривой. Функция на [ 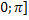 убывает от 1 до -1 на
убывает от 1 до -1 на 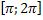 возрастает от -1 до 1. Функция на [
возрастает от -1 до 1. Функция на [ 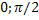 ] выпуклая, а на [
] выпуклая, а на [ 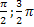 ] вогнутая, [
] вогнутая, [ 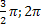 ] выпуклая.
] выпуклая.
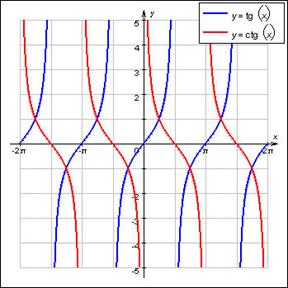
Функция y=tgx. Область определения функции – множество всех действительных чисел, кроме 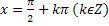 . Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс: x=kπ
. Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс: x=kπ 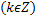 , эти же точки = точки перегиба. Функция на [
, эти же точки = точки перегиба. Функция на [ 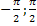 ] возрастает от -∞ до ∞. Функция вогнутая на
] возрастает от -∞ до ∞. Функция вогнутая на 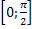 , выпуклая – на
, выпуклая – на 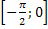 . Вертикальные асимптоты:
. Вертикальные асимптоты: 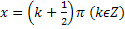 .
.
Функция y=ctgx. Область определения функции – множество всех действительных чисел, кроме 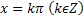 . Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс: x=k+
. Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс: x=k+  π
π 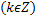 , эти же точки - точки перегиба. Функция на [
, эти же точки - точки перегиба. Функция на [ 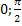 ]убывает от -∞ до ∞. Функция вогнутая на
]убывает от -∞ до ∞. Функция вогнутая на 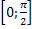 , выпуклая – на
, выпуклая – на 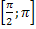 . Вертикальные асимптоты:
. Вертикальные асимптоты: 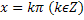 .
.
Графики функций:
Задания.
№ 1. Построить графики функций:
- y=cos2x
- y=sin(x-П/3)
- y=tgx/3
- y=ctg(2x+П/3)
№ 2. Вычислить:
1. 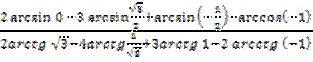
2. 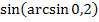
3. 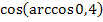
4. 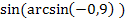
5. 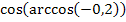
6. 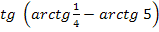
№ 3. Выяснить, какое из следующих двух ч




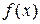 делится на многочлен
делится на многочлен 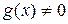 , если существует такой многочлен
, если существует такой многочлен 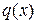 , что выполняется равенство
, что выполняется равенство 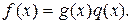
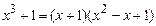 следует, что
следует, что 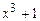 делится на многочлен
делится на многочлен 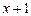 и на многочлен
и на многочлен 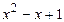 .
.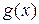 , а
, а 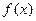 делится
делится 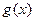 , а
, а 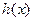 , то
, то 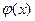 , то их сумма и разность также делятся на
, то их сумма и разность также делятся на 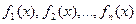 делится на
делится на 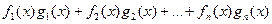 , где
, где 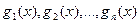 - произвольные многочлены.
- произвольные многочлены.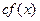 ,
, 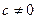 , и только они будут делителями многочлена
, и только они будут делителями многочлена 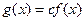 ,
, 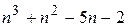 является простым.
является простым.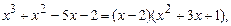
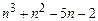 делится на
делится на 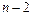 и на
и на 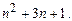 Следовательно, оно может быть простым только в случае, когда один из этих делителей равен 1 или –1, т.е. выполняется хотя бы одно из равенств
Следовательно, оно может быть простым только в случае, когда один из этих делителей равен 1 или –1, т.е. выполняется хотя бы одно из равенств 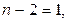
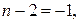
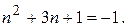
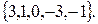
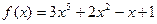 и
и 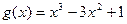
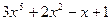 |
| 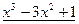
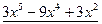
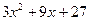
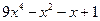
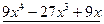
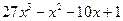
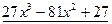

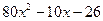
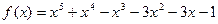 и
и 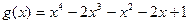
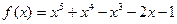 и
и 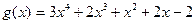
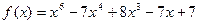 и
и 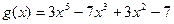
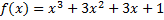 ,
, 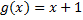 ;
;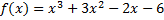 ,
, 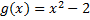 ;
;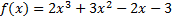 ,
, 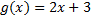 ;
;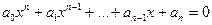
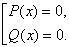
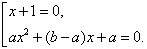
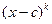 , но не делится на
, но не делится на 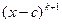 . Поэтому
. Поэтому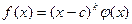 ,
,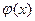 на x-c уже не делится. Число k называется кратностью корня c в многочлене f(x), а сам корень c – k- кратным корнем этого многочлена. Если k =1, то говорят, что корень с – простой.
на x-c уже не делится. Число k называется кратностью корня c в многочлене f(x), а сам корень c – k- кратным корнем этого многочлена. Если k =1, то говорят, что корень с – простой.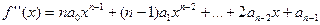
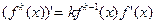
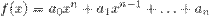
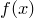 на
на 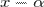 с остатком:
с остатком: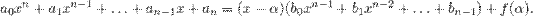
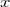 в левой и правой части:
в левой и правой части: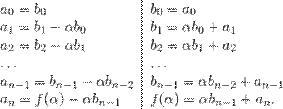
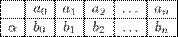
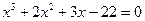
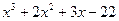 имеет корень 2. По теореме Безу f(x) делится на x-2, то есть имеет место равенство
имеет корень 2. По теореме Безу f(x) делится на x-2, то есть имеет место равенство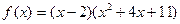 .
.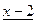
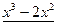
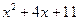
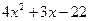
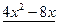
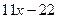
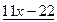
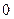
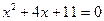 . Это уравнение не имеет действительных корней, так что x=2 – единственный действительный корень исходного уравнения.
. Это уравнение не имеет действительных корней, так что x=2 – единственный действительный корень исходного уравнения. многочлена
многочлена 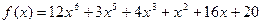
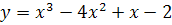
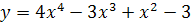
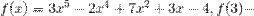
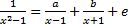 ;
;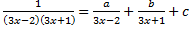 ;
;










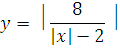
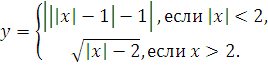
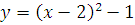
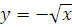
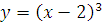
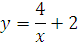
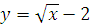
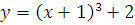

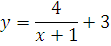
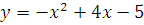
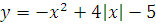
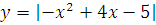
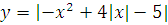
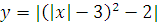
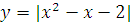
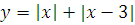
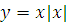
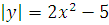
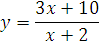
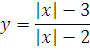
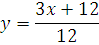
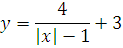
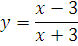
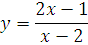
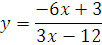
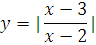
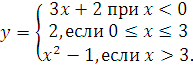

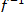 и называют обратной функцией. Функция у = f (х) при этом называется прямой функцией.
и называют обратной функцией. Функция у = f (х) при этом называется прямой функцией.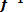 (у) называются взаимно обратными.
(у) называются взаимно обратными.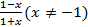
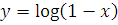
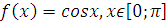
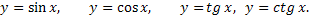
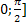 возрастает от 0 до 1 на
возрастает от 0 до 1 на 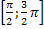 убывает от 1 до -1, на
убывает от 1 до -1, на 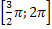 возрастает от -1 до 0. Функция на [
возрастает от -1 до 0. Функция на [ 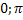 ] выпуклая, а на [
] выпуклая, а на [ 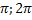 ] вогнутая.
] вогнутая.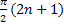 (nϵZ), эти точки являются и точками перегиба графика кривой. Функция на [
(nϵZ), эти точки являются и точками перегиба графика кривой. Функция на [ 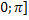 убывает от 1 до -1 на
убывает от 1 до -1 на 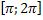 возрастает от -1 до 1. Функция на [
возрастает от -1 до 1. Функция на [ 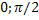 ] выпуклая, а на [
] выпуклая, а на [ 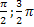 ] вогнутая, [
] вогнутая, [ 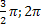 ] выпуклая.
] выпуклая.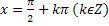 . Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс: x=kπ
. Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс: x=kπ 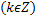 , эти же точки = точки перегиба. Функция на [
, эти же точки = точки перегиба. Функция на [ 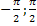 ] возрастает от -∞ до ∞. Функция вогнутая на
] возрастает от -∞ до ∞. Функция вогнутая на 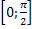 , выпуклая – на
, выпуклая – на 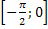 . Вертикальные асимптоты:
. Вертикальные асимптоты: 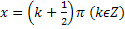 .
.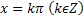 . Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс: x=k+
. Область значения [-∞,∞]. Функция нечетная, периодическая с периодом π. Точки пересечения в осью абсцисс: x=k+  π
π 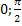 ]убывает от -∞ до ∞. Функция вогнутая на
]убывает от -∞ до ∞. Функция вогнутая на 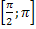 . Вертикальные асимптоты:
. Вертикальные асимптоты: 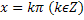 .
.