Случайные функции. Цепи Маркова

Пусть Т – некоторое множество действительных чисел. Если каждому значению поставлена в соответствие случайная величина X (t),то на множестве Т задана случайная функция X (t).

Если t – время, то случайная функция называется случайным процессом. Значение случайной функции X (t ₀)при t = t₀, где ,называется сечением. Каждое испытание дает конкретную функцию x (t), которая называется реализацией (траекторией) случайной функции.

При зафиксированном значении аргумента t случайная функция X (t) превращается в случайную величину – сечение случайной функции или процесса. Тогда X (t) в данный момент времени t определяется плотностью распределения р (x; t). Однако одномерные законы распределения и их числовые характеристики, вычисленные для одного момента времени (для одного сечения семейства реализаций) не могут оценивать характер изменения процесса во времени. Для этой цели используют характеристики связи между ординатами, взятыми в различные моменты времени. Наиболее полно эти связи характеризуются многомерной плотностью распределения f (x _l, x ₂,.., x_n; t _l, t ₂,.., t_n) п произвольных сечений процесса. Однако многомерная плотность распределения не всегда известна, поэтому для практических приложений случайные процессы характеризуются математическим ожиданием, дисперсией и корреляционной функцией.

Математическим ожиданием случайной функции X (t)называют неслучайную функцию т_х (t),которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения семейства реализаций случайной функции: и является средней траекторией для всех возможных реализаций.

Дисперсией случайной функции X (t)называют неслучайную функцию D_x (t),значение которой для каждого t равно дисперсии соответствующего сечения случайной функции: и характеризующей возможный разброс реализаций случайной функции относительно средней траектории.

Корреляционной функцией случайной функции X (t)называют неслучайную функцию двух аргументов K_x (t, t'),которая при каждой паре значений t, t' равна корреляционному моменту соответствующих сечений случайной функции:

Корреляционная функция характеризует степень зависимости между сечениями случайной функции, относящихся к различным t. Положительное значение корреляционной функции свидетельствует о том, что при увеличении (уменьшении) ординат процесса в сечении t всреднем увеличиваются (уменьшаются) ординаты при t'. Отрицательная корреляция означает увеличение (уменьшение) в среднем ординат в сечении t при их уменьшении (увеличении) в сечении t'.

Корреляционная функция является симметричной функцией своих аргументов, а ее ординаты по абсолютному значению не могут быть больше произведений среднеквадратичных отклонений в моменты времени t и t':

Процесс считается стационарным, если его многомерная плотность распределения не изменяется при сдвиге соответствующих моментов времени на любую величину. В рамках корреляционной теории, процесс считается стационарным, если его ковариационная функция M [ X (t)· X (t ')] не зависит от времени, а зависит только от разности ,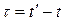

Корреляционная функция стационарного процесса по модулю не превосходит дисперсию:

Стационарный процесс у которого корреляционная функция стремится к нулю при называют эргодичным. Эргодические процессы представляют наибольший интерес для практических приложений, поскольку их характеристики, определяемые по семейству и по одной реализации совпадают: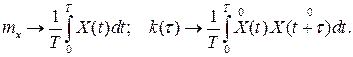

Марковскими случайными процессами называют такие процесса, у которых плотность совместного распределения произвольных двух сечений полностью определяют характер процессов, т.е. дальнейшее поведение процесса зависит только от значений, принятых процессом в настоящий момент времени, и не зависит от ранее принятых. Марковский случайный процесс, в котором сама функция принимает счетное множество возможных состояний (дискретные состояния) x _l, x ₂, x ₃,.., x_n,...,переход из одного состояния в другое происходит скачком под влиянием случайных факторов, называют цепями Маркова. Если переход из состояния в состояние происходит в дискретные моменты времени t ₁, t ₂, t ₃,..., t_n,..., тo такой процесс называют дискретными цепями Маркова. Если переходы возможны в любой момент времени, то процесс называют непрерывными цепями Маркова.

Вероятность того, что дискретная цепь Маркова в момент времени t_i примет значение х_п при условии, что в момент времени t _{i -1}, она имела значение х_т, называют вероятностью перехода из состояния в состояние Р_тп (t_{i -1,} t_i). Если эта вероятность зависит от длины промежутка времени и не зависит от начала отсчета времени, т.е. не зависит от номера шага, то такую цепь Маркова называют однородной:

Дискретные цепи Маркова однозначно определяются либо матрицей переходов

или графом состояний

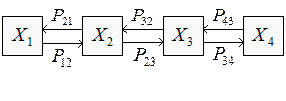
Вектором вероятностей (безусловной вероятностью) состояния цепи Маркова называют вероятности р_п (t_i) того, что в момент времени t_i цепь примет значение х_п,которая представляет собой матрицу-строку:

, где

Вектор вероятностей состояния однородной цепи Маркова после i этапов однозначно определяется вектором вероятностей P (t ₀) в начальный момент времени и матрицей переходов :

.

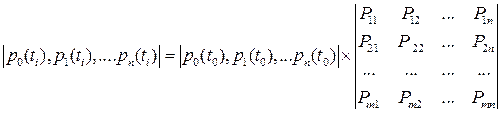Если в цепи Маркова 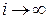, то вектор вероятностей состояния превращается в вектор финальной (стационарной) вероятности [ р ₀, p ₁,..., p_n ], определяемый из однородной системы (n +1)-го уравнения:

Учитывая, что р ₀ +p _l +... +p_n = 1 и заменяя этим соотношением одно из вышеприведенных уравнений в системе, находим искомые финальные (стационарные) вероятности однородной цепи Маркова.

Для непрерывных цепей Маркова возможности перехода из состояния х_m в состояние х_п за время Δ t оценивается плотностью вероятностей перехода λ_тп:

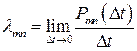; при условии, что .

Если λ_тп не зависит от времени, то непрерывная цепь Маркова называется однородной.

Для непрерывных цепей Маркова вектор вероятностей состояния есть функция времени и определяется путем решения системы дифференциальных уравнений, которые составляются по графу состояния цепи Маркова по следующим правилам:

- в левой части каждого уравнения стоят производные по времени вероятностей состояния цепи;

- правая часть этих уравнений содержит столько членов, сколько переходов (стрелок на графе) связанно с данным состоянием;

- каждый член правой части уравнений равен произведению плотности вероятностей перехода, соответствующей данной стрелки графа состояния, умноженной на вероятность того состояния из которого исходит стрелка;

- каждый член правой части уравнений имеет знак «минус», если стрелка графа состояния входит в данное состояния и знак «плюс», если стрелка выходит из данного состояния.

Например: Имеем граф состояния однородной непрерывной цепи Маркова:

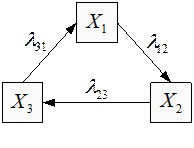
Для этого графа составляем систему уравнений по вышеуказанным правилам:

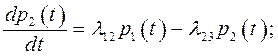
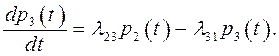
Учитывая, что p _l(t)+ p ₂(t)+ p ₃(t)=1, известными методами находят p _l(t), p ₂(t), p ₃(t).

В случае, когда нас интересуют вероятности состояния непрерывных цепей Маркова по истечению длительного промежутка времени (установившейся процесс 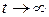), то решение системы получают путем записи в левой части системы дифференциальных вместо производных нулей, т.е.

Задачи

10.1. Имеются три конкурирующих изделия х ₁, х ₂, х ₃.Для определения спроса на эти изделия произведен в некоторый момент времени опрос 1000 человек. Оказалось, что x ₁ покупают 500 человек, х ₂ – 200, х ₃ – 300. По истечению месяца оказалось, что из 500 человек, покупавших изделие х ₁, 450 человек продолжали покупать это изделие, 40 человек стали покупать изделие х ₂,10 человек – изделие х ₃.Из 200 человек, покупавших изделие х ₂, 80 стали покупать изделие х ₁, 60 – изделие х ₃, 60 продолжали покупать изделие х ₂.Из 300 человек, покупавших изделие х ₃, 60 продолжали покупать это изделие, 210 стали покупать изделие х ₁, а 30 – изделие х ₂. Определить какое изделие по истечению месяца, двух и пяти лет будет пользоваться наибольшим спросом.

Решение: Предположим, что поведение покупателей в каждый следующий месяц обусловлено их поведением в предыдущий месяц, то мы можем представить эту задачу в виде дискретной однородной цепи Маркова с тремя состояниями.

В момент времени t ₀(проведение опроса) вероятности состояния системы (вероятности спроса на изделия) имели следующие значения:

P (t ₀)=|0,5;0,2;0,3|.

Определим параметры матрицы переходов (вероятности перехода из состояния в состояние):

; ; ;

; ; ;

; ;

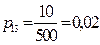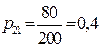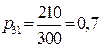Найдем вектор вероятностей состояния цепи по истечению одного месяца:

Т.е. наибольшим спросом по истечению одного месяца будет пользоваться изделие x ₁, (p ₁(t _l) = 0,74), изделия х ₂, х ₃ одинаковым спросом (p ₂(t ₁) = p ₃(t ₁) = 0,13).

По истечению двух месяцев:

наибольшим спросом так же будет пользоваться изделие x ₁. По истечению более длительного срока, оценку спроса можно произвести исходя из того, что для данной цепи условия эргодичности выполняется. При получаем следующую систему уравнений:

p ₁ = 0,9 p ₁ + 0,4 p ₂ + 0,7 p ₃;

p ₂ = 0,08 p ₁ + 0,3 p ₂ + 0,1 p ₃;

p ₃ = 0,07 p ₁ + 0,3 p ₂ + 0,2 p ₃.

Заменив одно из уравнений вышеуказанной системы уравнением p ₁ +p ₂ +p ₃ = 1, получим искомые финишные (стационарные) вероятности нашей цепи Маркова p ₁ = 0,84; p ₂ = 0,1; p ₃ = 0,06.

10.2. В городе N три местных супермаркета А, В, С,конкурируют между собой и относительно их фирма по изучения рынка выявила следующие факты. На 1 января каждый магазин имел равное число покупателей. За предыдущие 12 месяцев в среднем за месяц:

- Магазин А сохранил 80% своих покупателей и получил 10%
покупателей магазина В и 2% покупателей магазина С;

- Магазин В сохранил 70% своих покупателей и получил 14%
покупателей магазина А и 8% покупателей магазина С;

- Магазин С сохранил 90% своих покупателей, получил 6% покупателей магазина А и 20% покупателей магазина В.

Составьте матрицу перехода для средних ежемесячных изменений. Если предположить, что общее число покупателей в городе N постоянно, то какую долю от их числа имеет каждый магазин с 1 февраля, учитывая, что составленная матрица переходов верна в течение января.

10.3. Компания по прокату автомобилей выдает автомобили в трех аэропортах. Клиенты возвращают автомобили в эти аэропорты в соответствии с таблицей вероятностей:

 

Куда Откуда	А	В	С
А	0,8	0,2
В	0,2		0,8
С	0,2	0,2	0,6

 

а) Вычислить вектор X' Марковской цепи, удовлетворяющий равенству X'=Х'Р, . Представляет ли этот вектор стационарные вероятности?

б) В каком аэропорту следует построить авторемонтную станцию?

10.4. Некоторая фирма находиться в одном из двух состояний: «получает прибыль» или «нуждается в диверсификации своей деятельности». Если фирма получает прибыль сегодня, вероятность того, что она будет получать прибыль завтра, равна 0,7, а вероятность того, что она завтра будет нуждаться в диверсификации своей деятельности, равна 0,3. Если же фирма нуждается в диверсификации своей деятельности сегодня, то вероятность того, что она будет работать с прибылью завтра равна 0,6, а вероятность того, что она будет нуждаться в диверсификации своей деятельности, равна 0,4. Определить вероятность работы фирмы с прибылью через три дня.