Определение. Множество  называется областью сходимости, если для каждой точки
называется областью сходимости, если для каждой точки 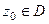 соответствующий числовой ряд
соответствующий числовой ряд 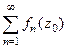 сходится.
сходится.
Если ряды из комплексных функций, то  это область в плоскости, например круг, а если действительные функции, то
это область в плоскости, например круг, а если действительные функции, то  какой-либо интервал или объединение интервалов на действительной прямой.
какой-либо интервал или объединение интервалов на действительной прямой.
Метод нахождения области сходимости. применять те же самые признаки (Даламбера, Коши) но только для «произвольного» 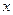 .
.
То есть, в пределе так до конца и остаётся переменная. а затем решить неравентво.
Пример. Найти область сходимости ряда  .
.
 =
=  =
=  < 1.
< 1.
Если раньше, в теме «числовые ряды» мы просто получали в пределе какое-то число 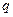 и могли сказать, что оно больше либо меньше 1, то теперь получили функцию от
и могли сказать, что оно больше либо меньше 1, то теперь получили функцию от 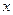 , т.е. при одних значениях больше 1, а при других меньше. Надо решить неравенство и найти, где это выражение меньше 1.
, т.е. при одних значениях больше 1, а при других меньше. Надо решить неравенство и найти, где это выражение меньше 1.




 это интервал, где есть абсолютная сходимость.
это интервал, где есть абсолютная сходимость.
Там, где  , то есть
, то есть  ряд расходится.
ряд расходится.
При  признак Даламбера не даёт ответа, надо проводить исследование поведения ряда в граничных точках в ручном режиме.
признак Даламбера не даёт ответа, надо проводить исследование поведения ряда в граничных точках в ручном режиме.
Подставим  . Получим ряд
. Получим ряд  он расходится.
он расходится.
Подставим  . Получим ряд
. Получим ряд 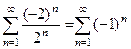 он тоже расходится, не выполнен необходимый признак, т.е. слагаемые не уменьшаются к 0. Итак, граничные точки не добавятся к области сходимости, и ответ остаётся таким:
он тоже расходится, не выполнен необходимый признак, т.е. слагаемые не уменьшаются к 0. Итак, граничные точки не добавятся к области сходимости, и ответ остаётся таким:  .
.
Пример. Найти область сходимости ряда  .
.
 =
= 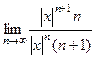 =
=  =
=  .
.
Теперь решим неравенство 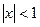 . Это означает
. Это означает 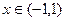 - вот область абсолютной сходимости.
- вот область абсолютной сходимости.
Исследуем граничные точки.
При 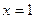 : ряд
: ряд  , он расходится (гармонический ряд, изучали ранее). При
, он расходится (гармонический ряд, изучали ранее). При  : ряд
: ряд  , знакочередующийся, сходится по признаку Лейбница, но условно, так как
, знакочередующийся, сходится по признаку Лейбница, но условно, так как  это и есть ряд из его модулей а он расходится. итак, ответ: область сходимости
это и есть ряд из его модулей а он расходится. итак, ответ: область сходимости  .
.
Пример. Найти область сходимости  .
.
Решение. Извлечём корень n порядка из модуля. Получим 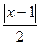 .
.
Решим неравенство 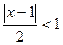 , т.е.
, т.е. 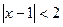 , что равносильно
, что равносильно  , то есть
, то есть  . Решением неравенства будет множество
. Решением неравенства будет множество  . Подставляя граничные точки, получаем расходимость:
. Подставляя граничные точки, получаем расходимость:
При  :
: 
слагаемые не стремятся к 0, не выполнен необходимый признак, ряд расходится.
При  :
:  по той же причине ряд расходится.
по той же причине ряд расходится.
Ответ. область сходимости  .
.
Степенные ряды.
Общий вид степенного ряда:  , где
, где  числовые коэффициенты. В этом ряде только положительные степени одного и того же выражения
числовые коэффициенты. В этом ряде только положительные степени одного и того же выражения  и константа (что получается при нулевой степени). Возможно, что часть коэффициентов равна 0, то есть некоторые степени пропущены.
и константа (что получается при нулевой степени). Возможно, что часть коэффициентов равна 0, то есть некоторые степени пропущены.
Теорема 1 (Абеля). 1) Если ряд 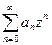 сходится в точке
сходится в точке  , то он сходится в любой точке
, то он сходится в любой точке 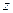 , для которой
, для которой 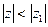 , причём абсолютно.
, причём абсолютно.
2) Если ряд 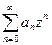 расходится в точке
расходится в точке  то он расходится в любой точке, для которой
то он расходится в любой точке, для которой  .
.
Доказательство. Сходимость в точке  ряда
ряда 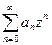 означает, что
означает, что  . Если этот ряд сходится, то согласно необходимому признаку, слагаемые стремятся к 0. Тогда среди них есть максимальное по модулю, и таким образом, они ограничены в совокупности, некоторой константой
. Если этот ряд сходится, то согласно необходимому признаку, слагаемые стремятся к 0. Тогда среди них есть максимальное по модулю, и таким образом, они ограничены в совокупности, некоторой константой  , т.е.
, т.е.  .
.
Теперь рассмотрим ряд 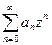 в произвольной точке
в произвольной точке 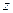 , которая ближе к началу координат на комплексной плоскости.
, которая ближе к началу координат на комплексной плоскости.

Итак, взяли точку, для которой 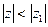 . Тогда
. Тогда 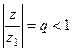 .
.
Для доказательства абсолютной сходимости, рассмотрим ряд, состоящий из модулей:  =
=  (домножили и поделили). При этом
(домножили и поделили). При этом  . Тогда
. Тогда 

 =
=  =
=  =
=  то есть меньше или равно некоторой сходящейся геометрической прогрессии.
то есть меньше или равно некоторой сходящейся геометрической прогрессии.
Итак, 

 , то есть ряд
, то есть ряд  сходится, то есть
сходится, то есть 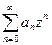 сходится абсолютно.
сходится абсолютно.
Пункт 2. Нужно доказать, что если ряд 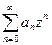 расходится в точке
расходится в точке  , то он расходится в любой точке, которая дальше от начала координат. Допустим, что в
, то он расходится в любой точке, которая дальше от начала координат. Допустим, что в  расходимость, но есть сходимость в какой-то более далёкой точке
расходимость, но есть сходимость в какой-то более далёкой точке 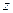 . Но тогда это противоречило бы уже доказанному пункту 1, так как из сходимости в
. Но тогда это противоречило бы уже доказанному пункту 1, так как из сходимости в 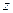 следовала бы сходимость в более близкой к началу координат точке
следовала бы сходимость в более близкой к началу координат точке  .
.
Следствие. Область сходимости степенного ряда есть круг.
(в R интервал)
Действительно, по теореме 1, во всех более близких к центру точках - сходимость, а если нашлась точка, где ряд расходится, то сразу же во всех, более далёких от центра - тоже расходимость. Тогда область есть круг.
Примечание. Центр круга сходимости это точка  . Мы доказали теорему Абеля для центра в точке 0 для простоты и ясности обозначений, но полностью аналогичные выкладки верны и для центра в любой другой точке.
. Мы доказали теорему Абеля для центра в точке 0 для простоты и ясности обозначений, но полностью аналогичные выкладки верны и для центра в любой другой точке.
Но на самом деле, выше был рассмотрен случай в комплексной плоскости. А для рядов из действительных степенных функций  , пересечение круга с действительной прямой порождает симметричный интервал с центром в точке
, пересечение круга с действительной прямой порождает симметричный интервал с центром в точке  . Таким образом, область сходимости это интервал
. Таким образом, область сходимости это интервал  .
.
Теорема 2. Формулы радиуса сходимости степенного ряда:
 и
и 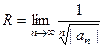 .
.
Заметим, что в этих формулах  обозначает не просто n-е слагаемое, а лишь его часть, сам числовой коэффициент без степенной функции, а дроби обратные по сравнению с теми, как в признаках Даламбера или Коши. Рассмотрим доказательство, чтобы понять, почему так происходит.
обозначает не просто n-е слагаемое, а лишь его часть, сам числовой коэффициент без степенной функции, а дроби обратные по сравнению с теми, как в признаках Даламбера или Коши. Рассмотрим доказательство, чтобы понять, почему так происходит.
Доказательство.
Применим к степенному ряду 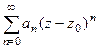 признак Даламбера.
признак Даламбера.
 =
=  , из чего следует
, из чего следует  , т.е.
, т.е.  .
.
Вот и получилось условие, задающее круг в комплексной плоскости. Это можно считать также вторым, независимым доказательством того следствия из теоремы Абеля, где говорилось, что область сходимости есть круг.
Докажем вторую формулу.
Применим к степенному ряду 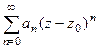 признак Коши.
признак Коши.
 =
= 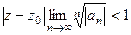 , т.е.
, т.е.  , т.е.
, т.е.
 .
.
Пример. Найти радиус сходимости ряда  .
.
Отбросим степенную часть и извлечём коэффициент.
 , тогда
, тогда  . Тогда
. Тогда  =
=  .
.
Можно считать и по второй формуле: 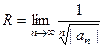 =
=  .
.
Итак, центр в точке 1, а радиус 2, то есть область сходимости - интервал  . Примечание. Чуть раньше мы решали этот же пример другим способом, просто по признаку Даламбера, а здесь по формулам радиуса R.
. Примечание. Чуть раньше мы решали этот же пример другим способом, просто по признаку Даламбера, а здесь по формулам радиуса R.
Пример. Найти радиус и область сх. ряда  .
.
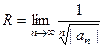 =
=  . R=5, интервал сходимости
. R=5, интервал сходимости 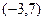 .
.



 называется областью сходимости, если для каждой точки
называется областью сходимости, если для каждой точки 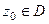 соответствующий числовой ряд
соответствующий числовой ряд 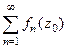 сходится.
сходится.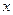 .
. .
. =
=  =
=  < 1.
< 1.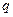 и могли сказать, что оно больше либо меньше 1, то теперь получили функцию от
и могли сказать, что оно больше либо меньше 1, то теперь получили функцию от 


 это интервал, где есть абсолютная сходимость.
это интервал, где есть абсолютная сходимость. , то есть
, то есть  ряд расходится.
ряд расходится. признак Даламбера не даёт ответа, надо проводить исследование поведения ряда в граничных точках в ручном режиме.
признак Даламбера не даёт ответа, надо проводить исследование поведения ряда в граничных точках в ручном режиме. . Получим ряд
. Получим ряд  он расходится.
он расходится. . Получим ряд
. Получим ряд 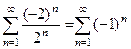 он тоже расходится, не выполнен необходимый признак, т.е. слагаемые не уменьшаются к 0. Итак, граничные точки не добавятся к области сходимости, и ответ остаётся таким:
он тоже расходится, не выполнен необходимый признак, т.е. слагаемые не уменьшаются к 0. Итак, граничные точки не добавятся к области сходимости, и ответ остаётся таким:  .
. =
= 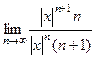 =
=  =
=  .
.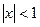 . Это означает
. Это означает 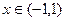 - вот область абсолютной сходимости.
- вот область абсолютной сходимости.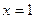 : ряд
: ряд  , он расходится (гармонический ряд, изучали ранее). При
, он расходится (гармонический ряд, изучали ранее). При  : ряд
: ряд  , знакочередующийся, сходится по признаку Лейбница, но условно, так как
, знакочередующийся, сходится по признаку Лейбница, но условно, так как  .
. .
.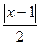 .
.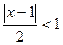 , т.е.
, т.е. 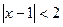 , что равносильно
, что равносильно  , то есть
, то есть  . Решением неравенства будет множество
. Решением неравенства будет множество  . Подставляя граничные точки, получаем расходимость:
. Подставляя граничные точки, получаем расходимость: :
: 
 по той же причине ряд расходится.
по той же причине ряд расходится. , где
, где  числовые коэффициенты. В этом ряде только положительные степени одного и того же выражения
числовые коэффициенты. В этом ряде только положительные степени одного и того же выражения  и константа (что получается при нулевой степени). Возможно, что часть коэффициентов равна 0, то есть некоторые степени пропущены.
и константа (что получается при нулевой степени). Возможно, что часть коэффициентов равна 0, то есть некоторые степени пропущены.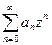 сходится в точке
сходится в точке  , то он сходится в любой точке
, то он сходится в любой точке 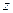 , для которой
, для которой 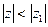 , причём абсолютно.
, причём абсолютно. .
. . Если этот ряд сходится, то согласно необходимому признаку, слагаемые стремятся к 0. Тогда среди них есть максимальное по модулю, и таким образом, они ограничены в совокупности, некоторой константой
. Если этот ряд сходится, то согласно необходимому признаку, слагаемые стремятся к 0. Тогда среди них есть максимальное по модулю, и таким образом, они ограничены в совокупности, некоторой константой  , т.е.
, т.е.  .
.
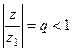 .
. =
=  (домножили и поделили). При этом
(домножили и поделили). При этом 
 =
=  =
=  =
=  то есть меньше или равно некоторой сходящейся геометрической прогрессии.
то есть меньше или равно некоторой сходящейся геометрической прогрессии. . Мы доказали теорему Абеля для центра в точке 0 для простоты и ясности обозначений, но полностью аналогичные выкладки верны и для центра в любой другой точке.
. Мы доказали теорему Абеля для центра в точке 0 для простоты и ясности обозначений, но полностью аналогичные выкладки верны и для центра в любой другой точке. , пересечение круга с действительной прямой порождает симметричный интервал с центром в точке
, пересечение круга с действительной прямой порождает симметричный интервал с центром в точке  . Таким образом, область сходимости это интервал
. Таким образом, область сходимости это интервал  .
. и
и 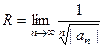 .
.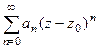 признак Даламбера.
признак Даламбера. =
=  , из чего следует
, из чего следует  , т.е.
, т.е.  .
. =
= 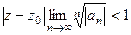 , т.е.
, т.е.  , т.е.
, т.е. .
. , тогда
, тогда  . Тогда
. Тогда  .
. .
. .
. . R=5, интервал сходимости
. R=5, интервал сходимости 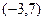 .
.


