Если дан ряд 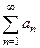 и при этом существует функция
и при этом существует функция 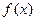 , такая, что при целых значениях она совпадает с членами этого ряда, т.е.
, такая, что при целых значениях она совпадает с членами этого ряда, т.е. 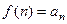 , то ряд
, то ряд 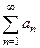 сходится тогда и только тогда, когда сходится несобственный интеграл
сходится тогда и только тогда, когда сходится несобственный интеграл 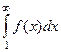 .
.
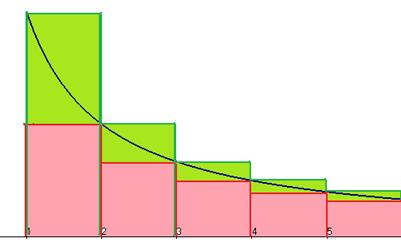
Доказательство. Рассмотрим чертёж. Высоты столбцов, расположенных выше графика (включающие в себя и зелёную и красную часть), это числа 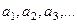 ., так как эти высоты
., так как эти высоты  и т.д. Сумма площадей этих столбцов, как раз и есть сумма ряда. И это больше, чем несобственный интеграл. В то же время столбцы, расположенные ниже графика (только красная часть на чертеже), имеют высоту
и т.д. Сумма площадей этих столбцов, как раз и есть сумма ряда. И это больше, чем несобственный интеграл. В то же время столбцы, расположенные ниже графика (только красная часть на чертеже), имеют высоту 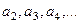 так как у первого из них высота
так как у первого из них высота 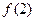 . Сумма их площадей это сумма остатка ряда без 1-го слагаемого. Но они все ниже графика, то есть их суммарная площадь меньше, чем несобственный интеграл.
. Сумма их площадей это сумма остатка ряда без 1-го слагаемого. Но они все ниже графика, то есть их суммарная площадь меньше, чем несобственный интеграл.
Итак, получили: 
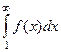
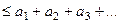
Правое неравенство означает: из того, что ряд сходится, следует, что несобственный интеграл сходится. А левое неравентство значит, что из сходимости интеграла следует сходимость остатка ряда, начиная со 2-го элемента. Но ведь сходимость остатка ряда равносильна сходимости самого ряда. Поэтому в итоге получается такой факт: ряд сходится тогда и только тогда, когда несобственный интеграл сходится.
Фактически, с помощью этой теоремы можно во многих случаях как бы заменять n на x, и исследовать не дискретные, а непрерывные величины, а это удобнее, т.к. можно интегрировать, применять первообразные, то есть гораздо больше способов для исследования.
Следствие. Ряды вида 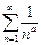 , сходятся при
, сходятся при 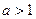 .
.
Доказательство очевидно: они эквивалентны интегралам  , про которые известно, что при
, про которые известно, что при 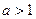 есть сходимость. Итак,
есть сходимость. Итак, 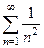 ,
, 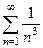 ,
, 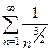 сходятся, а вот
сходятся, а вот  ,
, 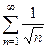 расходятся, здесь степень меньше или равна 1.
расходятся, здесь степень меньше или равна 1.
Но не всегда удаётся подобрать такую функцию, чтобы применить интегральный признак Коши. Например, в ряде может содержаться n!
Поэтому нужны и другие признаки.
Если исследовать внутреннюю структуру ряда, а именно отношение следующего слагаемого к предыдущему, то например, для геометрической прогресмсии это число всегда одно и то же 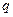 (называется знаменатель прогрессии). А вот если ряд не является прогресией, то оно как-то варьируется, для сходимости важно, чтобы оно оказалось меньше какого-то
(называется знаменатель прогрессии). А вот если ряд не является прогресией, то оно как-то варьируется, для сходимости важно, чтобы оно оказалось меньше какого-то 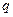 , то есть было меньше сходящейся прогрессии.
, то есть было меньше сходящейся прогрессии.
Теорема 3. Признак Даламбера в конечной (не-предельной) форме.
Если при всех 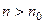 (то есть начиная с некоторого номера) выполняется условие
(то есть начиная с некоторого номера) выполняется условие 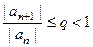 , то ряд абсолютно сходится.
, то ряд абсолютно сходится.
Доказательство. Во-первых, сходимость ряда равносильная сходимости его остатка, т.е. можем рассмотреть остаток ряда и заново перенумеровать члены ряда, начиная с  , поэтому можно доказывать даже при том условии, что
, поэтому можно доказывать даже при том условии, что 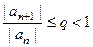 верно, даже начиная с первого номера. Обратите внимание, что условие
верно, даже начиная с первого номера. Обратите внимание, что условие 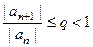 это не то же самое что
это не то же самое что 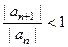 . В нашем случае все они меньше
. В нашем случае все они меньше 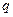 , которое само меньше 1, т.е. отделено от 1 некоторым расстоянимем на числовой прямой, т.е. предел этих величин не может быть равен 1, от любой из них до 1 остаётся некоторое расстояние
, которое само меньше 1, т.е. отделено от 1 некоторым расстоянимем на числовой прямой, т.е. предел этих величин не может быть равен 1, от любой из них до 1 остаётся некоторое расстояние 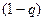 !
!
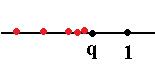
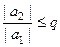

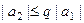 ,
,
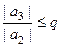

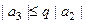

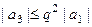 .
.
Продолжая таким образом, можно модуль каждого члена ряда оценить с помощью 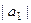 и какой-то степени числа
и какой-то степени числа 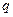 .
.
Итак, 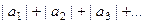
 =
=
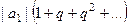 получилось, что ряд, состоящий из модулей, меньше некоторой убывающей геометрической прогрессии.
получилось, что ряд, состоящий из модулей, меньше некоторой убывающей геометрической прогрессии.
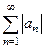 =
= 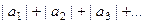
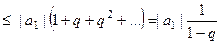 .
.
Итак, сумма меньше некоторого конечного числа, т.е. ряд 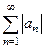 сходится, а значит, исходный ряд сходится абсолютно.
сходится, а значит, исходный ряд сходится абсолютно.
Теорема 4. Признак Даламбера в предельной форме.
Если 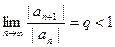 то ряд абсолютно сходится, если при этом
то ряд абсолютно сходится, если при этом 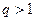 то ряд расходится.
то ряд расходится.
Доказательство. Следует из предыдущей теоремы таким образом. Если предел равен 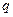 и оно строго меньше 1, то для всякого
и оно строго меньше 1, то для всякого  , начиная с некоторого номера, все отношения вида
, начиная с некоторого номера, все отношения вида 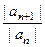 входят в окрестность
входят в окрестность 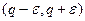 , а если заранее возьмём
, а если заранее возьмём 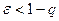 , то все эти элементы окажутся левее, чем
, то все эти элементы окажутся левее, чем 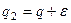 , при этом
, при этом 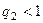 .
.
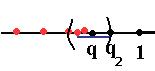
То есть, они всё равно будут отделены от 1 неким расстоянием. А тогда выполняются условия прошлой теоремы, и ряд абсолютно сходится.
Пример. Исследовать сходимость ряда  .
.
Поделим n+1 й член ряда на n-й. На практике лучше пользоваться предельным признаком, т.е. сразу перейти к пределу и получить 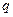 .
.
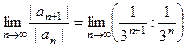 =
= 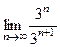 =
= 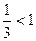 . Ответ: ряд сходится. Замечание. Сходимость здесь сразу абсолютная, так как все слагаемые и так положительны.
. Ответ: ряд сходится. Замечание. Сходимость здесь сразу абсолютная, так как все слагаемые и так положительны.
Пример. Исследовать сходимость ряда  .
.
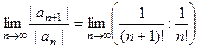 =
= 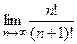 =
=  =
=
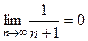 . Итак,
. Итак, 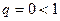 , ряд сходится.
, ряд сходится.
Замечание. Если было бы знакочередование, для признака Даламбера всё равно надо было бы рассмотреть по модулю, т.е. отбросить 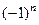 .
. 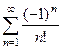 тоже сходится абсолютно. Знакочередование - вовсе не значит, что сходимость условная. Если исследовать здесь ряд даже без знакочередования, то он сходится.
тоже сходится абсолютно. Знакочередование - вовсе не значит, что сходимость условная. Если исследовать здесь ряд даже без знакочередования, то он сходится.
Теорема 5. Радикальный признак Коши в конечной форме.
Если при всех 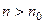 выполнено условие
выполнено условие 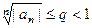 , то ряд
, то ряд 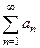 абсолютно сходится.
абсолютно сходится.
Доказательство. Если 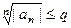 , то
, то 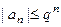 . Таким образом, начиная с некоторого номера, остаток ряда меньше или равен, чем убывающая геометрическая прогрессия.
. Таким образом, начиная с некоторого номера, остаток ряда меньше или равен, чем убывающая геометрическая прогрессия.
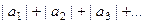
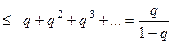 . Эта сумма конечна, то есть ряд абсолютно сходится.
. Эта сумма конечна, то есть ряд абсолютно сходится.
Теорема 6. Радикальный признак Коши в предельной форме.
Если 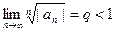 то ряд абсолютно сходится, если
то ряд абсолютно сходится, если 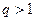 расходится.
расходится.
Доказательство следует из предыдущей теоремы, аналогично тому, как Т.4 из Т.3.
Пример. Выяснить сходимость ряда  .
.
Рассмотрим 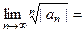
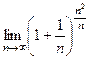 =
= 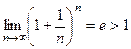 (использовали 2-й замеч. предел) ряд расходится.
(использовали 2-й замеч. предел) ряд расходится.
Замечание. При 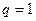 признак Даламбера и радикальный признак Коши не дают никакого ответа, в этом случае надо применять какие-либо другие признаки.
признак Даламбера и радикальный признак Коши не дают никакого ответа, в этом случае надо применять какие-либо другие признаки.
ЛЕКЦИЯ № 11. 25. 04. 2017
Далее следует серия признаков, основанных не на внутренней структуре ряда, а на сравнении с каким-то внешним, «эталонным» рядом.



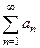 и при этом существует функция
и при этом существует функция 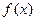 , такая, что при целых значениях она совпадает с членами этого ряда, т.е.
, такая, что при целых значениях она совпадает с членами этого ряда, т.е. 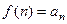 , то ряд
, то ряд 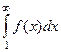 .
.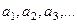 ., так как эти высоты
., так как эти высоты  и т.д. Сумма площадей этих столбцов, как раз и есть сумма ряда. И это больше, чем несобственный интеграл. В то же время столбцы, расположенные ниже графика (только красная часть на чертеже), имеют высоту
и т.д. Сумма площадей этих столбцов, как раз и есть сумма ряда. И это больше, чем несобственный интеграл. В то же время столбцы, расположенные ниже графика (только красная часть на чертеже), имеют высоту 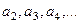 так как у первого из них высота
так как у первого из них высота 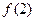 . Сумма их площадей это сумма остатка ряда без 1-го слагаемого. Но они все ниже графика, то есть их суммарная площадь меньше, чем несобственный интеграл.
. Сумма их площадей это сумма остатка ряда без 1-го слагаемого. Но они все ниже графика, то есть их суммарная площадь меньше, чем несобственный интеграл.

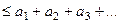
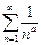 , сходятся при
, сходятся при 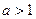 .
. , про которые известно, что при
, про которые известно, что при 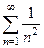 ,
, 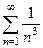 ,
, 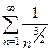 сходятся, а вот
сходятся, а вот  ,
, 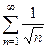 расходятся, здесь степень меньше или равна 1.
расходятся, здесь степень меньше или равна 1.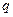 (называется знаменатель прогрессии). А вот если ряд не является прогресией, то оно как-то варьируется, для сходимости важно, чтобы оно оказалось меньше какого-то
(называется знаменатель прогрессии). А вот если ряд не является прогресией, то оно как-то варьируется, для сходимости важно, чтобы оно оказалось меньше какого-то 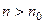 (то есть начиная с некоторого номера) выполняется условие
(то есть начиная с некоторого номера) выполняется условие 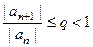 , то ряд абсолютно сходится.
, то ряд абсолютно сходится. , поэтому можно доказывать даже при том условии, что
, поэтому можно доказывать даже при том условии, что 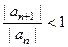 . В нашем случае все они меньше
. В нашем случае все они меньше 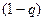 !
!
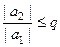

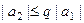 ,
,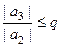
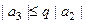
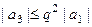 .
.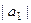 и какой-то степени числа
и какой-то степени числа 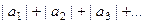
 =
=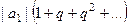 получилось, что ряд, состоящий из модулей, меньше некоторой убывающей геометрической прогрессии.
получилось, что ряд, состоящий из модулей, меньше некоторой убывающей геометрической прогрессии.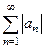 =
= 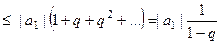 .
.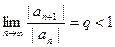 то ряд абсолютно сходится, если при этом
то ряд абсолютно сходится, если при этом 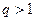 то ряд расходится.
то ряд расходится. , начиная с некоторого номера, все отношения вида
, начиная с некоторого номера, все отношения вида 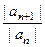 входят в окрестность
входят в окрестность 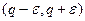 , а если заранее возьмём
, а если заранее возьмём 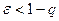 , то все эти элементы окажутся левее, чем
, то все эти элементы окажутся левее, чем 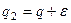 , при этом
, при этом 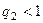 .
.
 .
.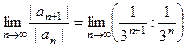 =
= 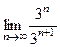 =
= 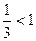 . Ответ: ряд сходится. Замечание. Сходимость здесь сразу абсолютная, так как все слагаемые и так положительны.
. Ответ: ряд сходится. Замечание. Сходимость здесь сразу абсолютная, так как все слагаемые и так положительны. .
.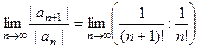 =
= 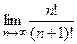 =
=  =
=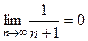 . Итак,
. Итак, 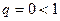 , ряд сходится.
, ряд сходится.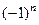 .
. 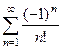 тоже сходится абсолютно. Знакочередование - вовсе не значит, что сходимость условная. Если исследовать здесь ряд даже без знакочередования, то он сходится.
тоже сходится абсолютно. Знакочередование - вовсе не значит, что сходимость условная. Если исследовать здесь ряд даже без знакочередования, то он сходится.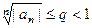 , то ряд
, то ряд 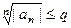 , то
, то 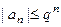 . Таким образом, начиная с некоторого номера, остаток ряда меньше или равен, чем убывающая геометрическая прогрессия.
. Таким образом, начиная с некоторого номера, остаток ряда меньше или равен, чем убывающая геометрическая прогрессия.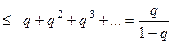 . Эта сумма конечна, то есть ряд абсолютно сходится.
. Эта сумма конечна, то есть ряд абсолютно сходится.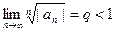 то ряд абсолютно сходится, если
то ряд абсолютно сходится, если  .
.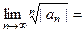
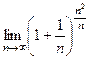 =
= 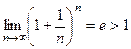 (использовали 2-й замеч. предел) ряд расходится.
(использовали 2-й замеч. предел) ряд расходится.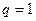 признак Даламбера и радикальный признак Коши не дают никакого ответа, в этом случае надо применять какие-либо другие признаки.
признак Даламбера и радикальный признак Коши не дают никакого ответа, в этом случае надо применять какие-либо другие признаки.


