

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Пример.  правая полуплоскость.
правая полуплоскость.
Пример.  верхняя полуплоскость.
верхняя полуплоскость.
Пример.  - окружность радиуса R вокруг начала координат.
- окружность радиуса R вокруг начала координат.
Пример. 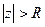 - круг радиуса R вокруг начала координат.
- круг радиуса R вокруг начала координат.
Пример.  это круг радиуса 1 вокруг точки
это круг радиуса 1 вокруг точки  . Это неравенство задаёт следующее условние: удаление числа
. Это неравенство задаёт следующее условние: удаление числа 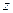 от фиксированного числа
от фиксированного числа  не превышает 1. Можно непосредственно преобразовать в уравнение круга в плоскости:
не превышает 1. Можно непосредственно преобразовать в уравнение круга в плоскости: 







 а это уравнение круга, центр которого в точке (0,1), то есть как раз в точке
а это уравнение круга, центр которого в точке (0,1), то есть как раз в точке  . Чертёж:
. Чертёж:

Пример. 

 это круг радиуса 2 с центром в точке
это круг радиуса 2 с центром в точке  , то есть точке (1,1) в плоскости.
, то есть точке (1,1) в плоскости.
Пример. Множество 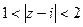 это кольцо вокруг точки
это кольцо вокруг точки  .
.
ГЛАВА 3. РЯДЫ.
Числовые ряды.
Пусть дана последовательность 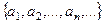 . Бесконечная сумма:
. Бесконечная сумма:  называется рядом.
называется рядом.
Если суммировать до какого-то номера n, то получается «частичная сумма»  . Часть, которая следует после слагаемого с номером n при этом называется остатком ряда.
. Часть, которая следует после слагаемого с номером n при этом называется остатком ряда. 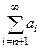 .
.
Если сумма ряда обозначена  , то:
, то: 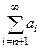 =
=  .
.
Для каждого ряда существует последовательность частичных сумм:
 ведь мы можем произвести конечное суммирование от 1-го до 1-го, затем от 1-го до 2-го, от 1-го до 3-го и так далее, и так для каждого n.
ведь мы можем произвести конечное суммирование от 1-го до 1-го, затем от 1-го до 2-го, от 1-го до 3-го и так далее, и так для каждого n.
Определение 1. Если сходится последовательность частичных сумм ряда, то и соответствующий ряд называется сходящимся.
Лемма. Сходимость ряда эквивалентна сходимости любого из его остатков.
Доказательство. 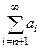 =
=  . Частичная сумма содержит конечное количество слагаемых, она точно является конечным числом. Обозначим остаток через
. Частичная сумма содержит конечное количество слагаемых, она точно является конечным числом. Обозначим остаток через  . Тогда
. Тогда  . Если
. Если  конечно, то сумма двух конечных чисел
конечно, то сумма двух конечных чисел  тоже конечна. А если сумма ряда, то есть
тоже конечна. А если сумма ряда, то есть  , есть конечное число, то
, есть конечное число, то 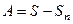 разность двух конечных чисел, а значит тже конечное число. Таким образом, имеет место и необходимость, и достаточность.
разность двух конечных чисел, а значит тже конечное число. Таким образом, имеет место и необходимость, и достаточность.
|
|
Более подробное определение сходимости с помощью  :
:
Определение 2. Ряд  называется сходящимся, если для всякого
называется сходящимся, если для всякого  существует такой номер
существует такой номер  , что
, что  .
.
Определения 1 и 2 эквивалентны: если, начиная с некоторого номера, сумма оставшихся элементов меньше любой заранее заданной погрешности, это и означает, что частичные суммы стабилизируются при 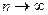 , то есть существует предел
, то есть существует предел  .
.
Пример. Рассмотрим убывающую геометрическую прогрессию - кстати, прогрессия это один из важных частных случаев ряда.
 Геометрическая интерпретация: возьмём квадрат
Геометрическая интерпретация: возьмём квадрат
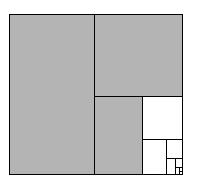
Если закрасить половину, затем четверть квадрата, и каждый раз половину того, что осталось до целого, то мы никогда не превысим площадь квадрата, а закрашенная площадь будет приближаться к 1.
Известна формула суммы бесконечной убывающей геометрической прогрессии: 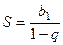 . В данном случае
. В данном случае  .
.
Для погрешности  найдём такой элемент, что частичная сумма отклоняется от суммы прогрессии менее чем на
найдём такой элемент, что частичная сумма отклоняется от суммы прогрессии менее чем на  , то есть остаток меньше
, то есть остаток меньше  .
.
 После 4-го элемента,
После 4-го элемента, 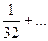
то есть для остатка, который тоже есть геометрическая прогрессия,

 .
.
Таким образом, после 4-го элемента, частичные суммы отклоняются от суммы менее чем на  .
.
Теорема 1. Необходимый признак сходимости.
Если ряд  сходится, то
сходится, то  .
.
Доказательство. Так как остаток ряда стремится к нулю, то есть сумма  =
= 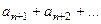 по модулю меньше чем
по модулю меньше чем  , то одно первое слагаемое из остатка - тем более, меньше чем
, то одно первое слагаемое из остатка - тем более, меньше чем  . Получается, что при росте номера
. Получается, что при росте номера  , а значит и общий член ряда уменьшается к нулю,
, а значит и общий член ряда уменьшается к нулю,  .
.
Замечание. Это необходимый, а не достаточный признак! Т.е. если  , это ещё не всегда означает, что ряд сходящийся, а вот если общий член ряда не стремится к нулю, то ряд расходится, то есть такие ряды даже не надо исследовать, про них сразу же известно, что сходимости нет. Сейчас мы увидим пример, где слагаемые стремятся к 0, а сходимости всё же нет.
, это ещё не всегда означает, что ряд сходящийся, а вот если общий член ряда не стремится к нулю, то ряд расходится, то есть такие ряды даже не надо исследовать, про них сразу же известно, что сходимости нет. Сейчас мы увидим пример, где слагаемые стремятся к 0, а сходимости всё же нет.
Гармонический ряд 
Доказательство его расходимости. Возьмём сумму от элемента номер n+1 до 2n. Докажем, что она больше 1/2, то есть для произвольного  , невозможно сделать её меньше, чем
, невозможно сделать её меньше, чем  .
.
|
|
Если была бы сходимость, то для любого  остаток, начиная с какого-то номера, меньше чем
остаток, начиная с какого-то номера, меньше чем  . Запишем для n даже не весь остаток ряда, а его часть, а именно, последующие n элементов.
. Запишем для n даже не весь остаток ряда, а его часть, а именно, последующие n элементов.

Наименьший элемент здесь  . Если мы заменим все слагаемые на него, то сумма лишь уменьшится, т.е.
. Если мы заменим все слагаемые на него, то сумма лишь уменьшится, т.е.
 >
> 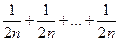 =
=  .
.
Итак, часть частичной суммы от номера n+1 до 2n больше, чем  , то есть не может быть меньше
, то есть не может быть меньше  . Определение сходимости не выполнено, ряд расходится. Здесь слагаемые уменьшаются к 0, но слишком медленно, недостаточно для сходимости.
. Определение сходимости не выполнено, ряд расходится. Здесь слагаемые уменьшаются к 0, но слишком медленно, недостаточно для сходимости.
Замечание. Тема «ряды» связана с темой «несобственные интегралы», там тоже рассматриваются только функции, стремящиеся к 0, и для них может быть либо сходимость, либо расходимость несобственного интеграла 1-го рода. Но там непрерывные, а здесь дискретные величины. Вспомним, что там тоже интеграл от 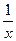 был расходящимся, аналогичное мы сейчас увидели для ряда
был расходящимся, аналогичное мы сейчас увидели для ряда 
Суммы рядов в некоторых случаях можно найти, используя формулу Тейлора. Вспомним, например, 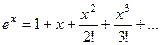 если здесь положим
если здесь положим 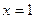 , то получается
, то получается  , то есть сумма
, то есть сумма  .
.
Вспомним разложение функции  , тогда при
, тогда при 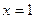 получается
получается  .
.
Если все слагаемые здесь были бы со знаком «+» то это был бы гармонический ряд, расходимость которого доказали ранее.
Получается, что если знаки чередуются, то сходимость может быть из-за частичной компенсации слагаемых, а если взять по модулю, то сходимости может и не быть. В связи с этим возникают такие понятия:
|
|
|

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!