Общий вид:  .
.
Если уравнение сведено к виду  то оно называется разрешённым относительно старшей (высшей) производной.
то оно называется разрешённым относительно старшей (высшей) производной.
Примеры дифференциальных уравнений 2 порядка из физики:
Уравнение колебаний  . Здесь чем больше координата, тем больше действует сила (ускорение) в противоположную сторону. Если координата
. Здесь чем больше координата, тем больше действует сила (ускорение) в противоположную сторону. Если координата  отрицательна, то сила действует в положительную сторону.
отрицательна, то сила действует в положительную сторону.
Методы понижения порядка.
Случай 1. Если в уравнении отсутствуют младшие порядки производных. Так, в уравнении  отсутствуют все производные до порядка k-1, в том числе 0-го порядка, а именно сама функция
отсутствуют все производные до порядка k-1, в том числе 0-го порядка, а именно сама функция  , и начинаются с порядка
, и начинаются с порядка  . В этом случае можно сдедать замену
. В этом случае можно сдедать замену 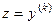 , то есть в качестве новой функции взять производную самого младшего порядка, которая есть в уравнении. Докажем, что в этом случае понизится на
, то есть в качестве новой функции взять производную самого младшего порядка, которая есть в уравнении. Докажем, что в этом случае понизится на  порядков и станет
порядков и станет  .
.
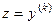



 и т.д.
и т.д.
Пример. Решить уравнение 2 порядка  .
.
Замена: 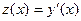 , тогда
, тогда  .
.
Уравнение сводится к виду  . Для
. Для 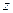 уравнение 1 порядка и решается обычными методами, изученными ранее.
уравнение 1 порядка и решается обычными методами, изученными ранее.










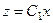 .
.
Вспомним о том, что  , то есть теперь, чтобы сделать обраную замену и восстановить
, то есть теперь, чтобы сделать обраную замену и восстановить  , надо 1 раз проинтегрировать.
, надо 1 раз проинтегрировать.
 =
=  . В общем решении здесь не одна, а две константы, вторая появляется из-за того, что интегрировали для обратной замены. А если уравнение 3 порядка, то будет 3 константы в общем решении.
. В общем решении здесь не одна, а две константы, вторая появляется из-за того, что интегрировали для обратной замены. А если уравнение 3 порядка, то будет 3 константы в общем решении.
Пример. Решить уравнение 3 порядка  .
.
Решение. Уравнение сводится к  но только в этом случае - заменой
но только в этом случае - заменой  , ведь самая младшая из производных, существующих в этом уравнении - вторая.
, ведь самая младшая из производных, существующих в этом уравнении - вторая.
Уравнение 1 порядка решается аналогично, и получаем 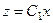 .
.
Теперь надо два раза вычислить первообразную:
 , тогда
, тогда  , а тогда
, а тогда  .
.
Случай 2. Если в уравнении содержится  и все порядки производных, но при этом нет переменной
и все порядки производных, но при этом нет переменной 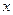 . Тип уравнения такой:
. Тип уравнения такой:  .
.
Например,  - уравнение колебательного процесса в физике.
- уравнение колебательного процесса в физике.
В этом случае замена  , то есть
, то есть  будет выступать в роли переменной, а
будет выступать в роли переменной, а  - в роли функции от
- в роли функции от  .
.
Естественно возникает вопрос: а существуют ли в принципе такие преобразования, не содержат ли они противоречия? Всегда ли можно выразить  как функцию от
как функцию от  ? Изучим этот вопрос подробнее. Оказывается, надо лишь найти обратную функцию и подставить её в производную
? Изучим этот вопрос подробнее. Оказывается, надо лишь найти обратную функцию и подставить её в производную  . Примеры:
. Примеры:
Пример 1.  ,
,  . Выразим
. Выразим  , и подставим в производную, тогда верно, что
, и подставим в производную, тогда верно, что  .
.
Пример 2.  ,
,  . Тогда
. Тогда  , и в итоге
, и в итоге  .
.
Как видите,  может быть записано не только как функция от
может быть записано не только как функция от 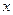 , но и как функция от
, но и как функция от  .
.
Итак, замена  . В данном случае,
. В данном случае,  не
не  , потому что фактически здесь была композиция:
, потому что фактически здесь была композиция:  , и следующую производную от неё надо вычислять именно как для композиции.
, и следующую производную от неё надо вычислять именно как для композиции.
Получается  .
.
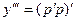 =
= 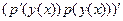
вычисляем производную произдведения двух сомножителей, причём в каждом из них ещё и композиция:

учитывая, что  , получится
, получится 
 .
.
1-я производная от  выражается через 0-ю производную от
выражается через 0-ю производную от  ,
,
2-я производная от  выражается максимум через 1-ю производную от
выражается максимум через 1-ю производную от  , 3-я производная от
, 3-я производная от  выражается через 2-ю, 1-ю и 0-ю производную от
выражается через 2-ю, 1-ю и 0-ю производную от  :
:



 .
.
Таким образом, доказали, что порядок при таком преобразовании обязательно понизится на 1 единицу.
Пример:  (уравнение колебаний).
(уравнение колебаний).
После замены, уравнение преобразуется к виду: 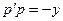 .
.
Сначала 1-й шаг: ищем неизвестную функцию  .
.




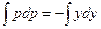



 .При этом
.При этом  , иначе справа всё выражение было бы отрицательно и не могло бы быть равно
, иначе справа всё выражение было бы отрицательно и не могло бы быть равно  . Если
. Если  , то эту константу можно представить в виде
, то эту константу можно представить в виде  . Итак,
. Итак,
 , то есть
, то есть  . Итак, мы нашли неизвестную функцию
. Итак, мы нашли неизвестную функцию  , то есть выполнели действия после замены. Теперь нужно сделать обратную замену, фактически для этого выполнить такой же по объёму 2-й шаг, решить новое дифференциальное уравнение. Ведь
, то есть выполнели действия после замены. Теперь нужно сделать обратную замену, фактически для этого выполнить такой же по объёму 2-й шаг, решить новое дифференциальное уравнение. Ведь  , то есть теперь надо решить уравнение:
, то есть теперь надо решить уравнение:
 .
.
2 шаг. Обратная замена.






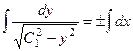





 . Здесь
. Здесь  называется амплитудой колебаний,
называется амплитудой колебаний, 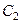 - фазой. Впрочем, при
- фазой. Впрочем, при  получается не синус, косинус, а именно, по формуле приведения
получается не синус, косинус, а именно, по формуле приведения  . Поэтому в решении есть и косинусы. Более того, мы могли при решении знак плюс-минус также перенести,
. Поэтому в решении есть и косинусы. Более того, мы могли при решении знак плюс-минус также перенести,  , тогда бы слева сразу получалось 2 варианта: или арксинус, или арккосинус.
, тогда бы слева сразу получалось 2 варианта: или арксинус, или арккосинус.
Ещё решение этого уравнения можно записать в виде:  .
.
На этом примере увидели, что уравнение  действительно является уравнением колебаний, то есть в его решении периодические функции.
действительно является уравнением колебаний, то есть в его решении периодические функции.
Здесь показаны лишь две основные наиболее известные замены.
Существуют и другие замены и преобразования, применяемые в разных частных случаях, например, иногда удобно поделить всё уравнение на  или на
или на  , чтобы оно упростилось.
, чтобы оно упростилось.



 .
. то оно называется разрешённым относительно старшей (высшей) производной.
то оно называется разрешённым относительно старшей (высшей) производной. . Здесь чем больше координата, тем больше действует сила (ускорение) в противоположную сторону. Если координата
. Здесь чем больше координата, тем больше действует сила (ускорение) в противоположную сторону. Если координата  отрицательна, то сила действует в положительную сторону.
отрицательна, то сила действует в положительную сторону. отсутствуют все производные до порядка k-1, в том числе 0-го порядка, а именно сама функция
отсутствуют все производные до порядка k-1, в том числе 0-го порядка, а именно сама функция  . В этом случае можно сдедать замену
. В этом случае можно сдедать замену 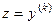 , то есть в качестве новой функции взять производную самого младшего порядка, которая есть в уравнении. Докажем, что в этом случае понизится на
, то есть в качестве новой функции взять производную самого младшего порядка, которая есть в уравнении. Докажем, что в этом случае понизится на  .
.

 и т.д.
и т.д. .
.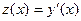 , тогда
, тогда  .
. . Для
. Для 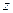 уравнение 1 порядка и решается обычными методами, изученными ранее.
уравнение 1 порядка и решается обычными методами, изученными ранее.




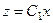 .
. , то есть теперь, чтобы сделать обраную замену и восстановить
, то есть теперь, чтобы сделать обраную замену и восстановить  =
=  . В общем решении здесь не одна, а две константы, вторая появляется из-за того, что интегрировали для обратной замены. А если уравнение 3 порядка, то будет 3 константы в общем решении.
. В общем решении здесь не одна, а две константы, вторая появляется из-за того, что интегрировали для обратной замены. А если уравнение 3 порядка, то будет 3 константы в общем решении. .
. , ведь самая младшая из производных, существующих в этом уравнении - вторая.
, ведь самая младшая из производных, существующих в этом уравнении - вторая. , тогда
, тогда  , а тогда
, а тогда  .
.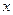 . Тип уравнения такой:
. Тип уравнения такой:  .
. - уравнение колебательного процесса в физике.
- уравнение колебательного процесса в физике. , то есть
, то есть  - в роли функции от
- в роли функции от  ,
,  . Выразим
. Выразим  , и подставим в производную, тогда верно, что
, и подставим в производную, тогда верно, что  .
. ,
,  . Тогда
. Тогда  , и в итоге
, и в итоге  .
. не
не  , потому что фактически здесь была композиция:
, потому что фактически здесь была композиция:  , и следующую производную от неё надо вычислять именно как для композиции.
, и следующую производную от неё надо вычислять именно как для композиции. .
.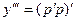 =
= 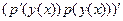

 , получится
, получится 
 .
. ,
,
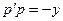 .
. .
.

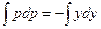

 .При этом
.При этом  , иначе справа всё выражение было бы отрицательно и не могло бы быть равно
, иначе справа всё выражение было бы отрицательно и не могло бы быть равно  . Если
. Если  . Итак,
. Итак, , то есть
, то есть  . Итак, мы нашли неизвестную функцию
. Итак, мы нашли неизвестную функцию  , то есть теперь надо решить уравнение:
, то есть теперь надо решить уравнение: .
.

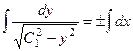


 . Здесь
. Здесь  называется амплитудой колебаний,
называется амплитудой колебаний, 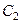 - фазой. Впрочем, при
- фазой. Впрочем, при  получается не синус, косинус, а именно, по формуле приведения
получается не синус, косинус, а именно, по формуле приведения  . Поэтому в решении есть и косинусы. Более того, мы могли при решении знак плюс-минус также перенести,
. Поэтому в решении есть и косинусы. Более того, мы могли при решении знак плюс-минус также перенести,  , тогда бы слева сразу получалось 2 варианта: или арксинус, или арккосинус.
, тогда бы слева сразу получалось 2 варианта: или арксинус, или арккосинус. .
.


