В идеальном одноатомном газе, находящемся в потенциальном (например, гравитационном) поле, имеет место определенная зависимость потенциальной энергии молекулы от координат U(x, y, z). Очевидно, в состоянии термодинамического равновесия в каждой точке газа (точнее, в достаточно малом его объеме) температура θ определяется лишь кинетической энергией хаотического движения молекул, т.е. распределением Fр(E), а не величиной U в этой точке. Покажем для газа, что распределение молекул по скоростям, а следовательно, и величины e и θ не зависят от величины U и, следовательно, от координат лишь при распределении Fm(E). Тем самым будет показано, что в этом случае формулировка 1 эквивалентна формулировке 2 (и 3), а также условием эквивалентности этих формулировок является наличие потенциальных сил, действующих на молекулы и приводящих к неоднородности газа.
В объеме dVo = dxo dyo dzo , где величина U равна нулю (напомним, что нулевое значение этой величины может быть выбрано произвольно),находится no dVo молекул газа, где no – их концентрация. Из этих молекул число молекул, компоненты скоростей которых находятся в интервалах dvox , dvoy , dvoz , определяется равенством:
dN(vo ) = no φ o (vo )dVo dvox dvoy dvoz , (2.1)
где φo(vo) – равновесное распределение молекул газа по векторам скоростей в этом объеме dVo .
Через некоторое время эти молекулы переместятся в пространстве и будут находиться в объеме dV = dxdydz и в фазовом объемеdVdvx dvy dvz (мы предполагаем, что в газе нет столкновений молекул). Число молекул в этом фазовом объеме определяется равенством:
dN(v) = n φ(v) dV dvx dvy dvz , (2.2)
где n – концентрация молекул в объеме dV, φ(v) – равновесное распределение молекул по векторам скоростей в этом объеме.
Наличие молекул (2.2) является лишь следствием наличия молекул (2.1). Поэтому
dN(vo ) = dN(v). (2.3)
По теореме Лиувилля элементарные фазовые объемы вдоль фазовой траектории равны:
dVo dvox dvoy dvoz = dVdvx dvy dvz . (2.4)
Подставляя (2.1) и (2.2) в (2.3), учитывая (2.4), имеем:
no φo(vo ) = n φ (v). (2.5)
Из закона сохранения энергии следует:
vo2 = v 2+ a, (2.6)
где a = 2 U / m.
Если φo(vo) = const при | vo| = const (равновозможность направлений движения молекул), то из (2.5) видно, что и φ(v) = const при | v| =const. Поэтому в (2.5) можно перейти от векторов скоростей к их модулям, что мы и сделаем. С учетом (2.6) из (2.5) следует:
 . (2.7)
. (2.7)
Если распределение не зависит от величины U, т.е.  , то продифференцировав (2.7) по v и по a получим два равенства, из которых имеем:
, то продифференцировав (2.7) по v и по a получим два равенства, из которых имеем:
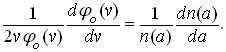 (2.8)
(2.8)
Левая часть равенства (2.8) зависит лишь от v, а правая – лишь от a. Поскольку эти переменные независимые, то это равенство возможно, если его левая и правая части равны некоторой постоянной величине. При этом решением дифференциального уравнения правой части является распределение Больцмана (барометрическая формула), а левой – распределение Максвелла. Это и требовалось показать.
Мы предполагали, что в газе нет межмолекулярных столкновений. В действительности они имеют место, однако в равновесном состоянии их можно не учитывать, т.к. в этом состоянии они не изменяют распределения молекул по скоростям.
Итак, лишь при одном (максвелловском) распределении молекул по скоростям это распределение и величины ε и θ не зависят от величины U и от координат, а градиент температуры равен нулю, что означает эквивалентность формулировок 1 и 2. В данном случае температура θ является абсолютной (статистической) температурой Т.
Как известно, при изотропности направлений, по которым могут двигаться молекулы, распределение их по абсолютным величинам скоростей определяется равенством:
f(v) = 4π v2φ(v). (2.9)
Из (2.7) и (2.9) следует:
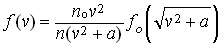 , (2.10)
, (2.10)
где fo(vо) – распределение молекул по абсолютным величинам скоростей, которое соответствует распределению φo(vо).
Условие нормировки имеет вид:
 (2.11)
(2.11)
Средняя кинетическая энергия молекул, имеющих потенциальную энергию U,
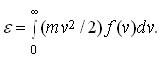 (2.12)
(2.12)
Подставляя (2.10) в (2.11) и (2.12), после последовательных двух замен переменной
v = (vo 2 – a)1/2, vo = (2E/m)1/2,
с учетом того, что fo(vo)dvo = Fo(E)dE, получим выражения для величин n и ε , зависящих от U, а также от распределения молекул по кинетическим энергиям Fo(E), соответствующего распределению fo(v):
 (2.13)
(2.13)
 (2.14)
(2.14)
Несложно показать, что если в (2.13) и (2.14) распределение Fo(E) совпадает с распределением Максвелла, то в газе будет распределение Больцмана, а величина e не зависит от величины U, т.е. формула Больцмана и независимость величины e (и температуры) от координат является следствием максвелловского распределения молекул по скоростям. Это означает, что экспериментальная проверка того, что равновесное распределение молекул по скоростям является распределением Максвелла (по сути, проверка формулировки 1), может быть заменена либо проверкой равенства нулю РГТ вдоль силовых линий потенциального поля (по сути, проверкой условия (В.4)), либо проверкой того, что имеет место распределение Больцмана (по сути, проверкой условия (В.5)). Отметим, что в распределение Больцмана (оно определяет зависимость концентрации молекул от потенциальной энергии молекулы) входит абсолютная температура Т, которая заведомо не должна зависеть от координат. В противном случае (если РГТ не равен нулю) нарушение распределения Больцмана будет автоматическим, т.е. будет автоматически нарушаться условие (В.5).
Отметим следующее. Величина e зависит от величины U, которая в однородном поле равна Pz. При увеличении силы P величина e и соответствующая ей температура θ, а также разность температур θ – θo , где θо – температура газа, молекулы которого имеют нулевую потенциальную энергию, не изменятся, если координату z уменьшить во столько же раз (при этом произведение Pz не изменится). Это означает, что при одном и том же отличии распределения Fo(E) от Fm(E) зависимости e (z) и θ(z) сжимаются прямо пропорционально действующим на молекулы силам, сохраняя при этом свою форму, а также РГТ может быть увеличен путем увеличения действующих на молекулы сил.
Из (2.13) и (2.14) видно, что если U(x, y, z) = const, то величины n и e (а следовательно, также температура θ) не зависят от координат, и РГТ равен нулю независимо от того, максвелловское распределение Fo(E) или нет. Это означает, что на эквипотенциальной поверхности формулировка 2 неэквивалентна формулировке 1.
Как известно, энтропия является мерой неупорядоченности в системе. Наибольшая неупорядоченность в газе имеет место при распределении Fm(E). Наименьшая неупорядоченность (при равной вероятности направлений, по которым могут двигаться молекулы) будет при одинаковых кинетических энергиях молекул, т.е. при распределении, являющимся дельта-функцией Дирака:
Fo(E) = δ(E – Eо ). (2.15)
Подставляя (2.15) в (2.14) и учитывая (2.13), имеем: e = e о - U. С учетом (В.2) в однородном поле будет градиент температуры:
(θo - θ)/z = 2P/(3k), (2.16)
где P – действующая на молекулу сила, равная mg, где g – ускорение свободного движения (падения). Несомненно, равновесное распределение (2.15) и соответствующий ему градиент (2.16) в действительности невозможны, как и невозможно большое отличие Fр(E) от Fm(E). При малом этом отличии РГТ будет намного меньше градиента (2.16), но из-за эквивалентности формулировок 1 и 2 он не будет равен нулю.
Подставляя (2.15) в (2.13), находим:
n = no(1 – U/Eo)1/ 2.
Эта формула отлична от распределения Больцмана (барометрической формулы).
В качестве примера вычислим равновесную разность температур для какого-нибудь распределения. Пусть
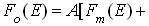
 , (2.17)
, (2.17)
где А - нормировочная постоянная, B - параметр, которым задается отличие распределения (2.17) от максвелловского, b - величина, определяемая из равенства средних кинетических энергий молекул при распределениях (2.17) и Fm(E), которое имеет вид:
 ,
,
где Em - наиболее вероятная кинетическая энергия поступательного движения молекул. Несложно показать, что b = 5/3, A = (1 + 0,4183B)-1. Если B < < 1, то
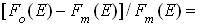
 . (2.18)
. (2.18)
Подставляя (2.17) в (2.14) и учитывая (2.13), найдем зависимость e (U). Если 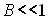 , то с учетом (В.2) искомая равновесная разность температур
, то с учетом (В.2) искомая равновесная разность температур
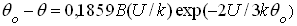 . (2.19)
. (2.19)
Например, если B = 0,001, то из (2.18) видно, что  порядка 0,01%. Такое малое отличие распределения Fo(E) от Fm(E) находится в пределах погрешностей вышеупомянутых экспериментов с молекулярными пучками по проверке совпадения распределения Fр(E) с распределением Fm(E). Вопрос о возможности в реальных системах отличия Fр(E) от Fm(E) на такую малую величину остаётся открытым. В однородном поле
порядка 0,01%. Такое малое отличие распределения Fo(E) от Fm(E) находится в пределах погрешностей вышеупомянутых экспериментов с молекулярными пучками по проверке совпадения распределения Fр(E) с распределением Fm(E). Вопрос о возможности в реальных системах отличия Fр(E) от Fm(E) на такую малую величину остаётся открытым. В однородном поле 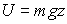 . Если m = 3× 10-26 кг (масса молекулы воды), g = 10 м/с2 (земное ускорение), z = 20 км, θo = 300 К (при этом
. Если m = 3× 10-26 кг (масса молекулы воды), g = 10 м/с2 (земное ускорение), z = 20 км, θo = 300 К (при этом 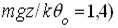 , то определяемая формулой (2.19) величина
, то определяемая формулой (2.19) величина  К, при этом градиент
К, при этом градиент  К/м, что намного (на четыре порядка) меньше градиента (2.16), который равен 0,014 К/м.
К/м, что намного (на четыре порядка) меньше градиента (2.16), который равен 0,014 К/м.
Таким образом, мы установили следующее. Условием эквивалентности формулировок 1 и 2 является наличие в системах потенциальных сил, действующих на частицы и приводящих к не равному нулю градиенту их концентрации. Равенство нулю градиента величины ε и, следовательно, температуры, а также распределение Больцмана являются следствием распределения Максвелла, т.е. условия (В.4) и (В.5) имеют место в случае совпадения распределения Fр(E) с распределением Fm(E) (формулы (2.13) и (2.14)). В связи с этим формулировка 1 (т.е. то, что имеет место совпадение Fр(E) с Fm(E)) может быть экспериментально проверена путём проверки условия (В.3) (первый метод проверки формулировки 1), а также путем проверки условия (В.5) (второй метод проверки формулировки 1) в системах, в которых выполняется условие эквивалентности формулировок 1 и 2.



 . (2.7)
. (2.7) , то продифференцировав (2.7) по v и по a получим два равенства, из которых имеем:
, то продифференцировав (2.7) по v и по a получим два равенства, из которых имеем: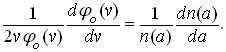 (2.8)
(2.8)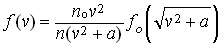 , (2.10)
, (2.10) (2.11)
(2.11)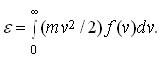 (2.12)
(2.12) (2.13)
(2.13) (2.14)
(2.14)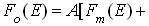
 , (2.17)
, (2.17) ,
,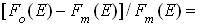
 . (2.18)
. (2.18)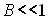 , то с учетом (В.2) искомая равновесная разность температур
, то с учетом (В.2) искомая равновесная разность температур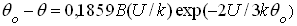 . (2.19)
. (2.19) порядка 0,01%. Такое малое отличие распределения Fo(E) от Fm(E) находится в пределах погрешностей вышеупомянутых экспериментов с молекулярными пучками по проверке совпадения распределения Fр(E) с распределением Fm(E). Вопрос о возможности в реальных системах отличия Fр(E) от Fm(E) на такую малую величину остаётся открытым. В однородном поле
порядка 0,01%. Такое малое отличие распределения Fo(E) от Fm(E) находится в пределах погрешностей вышеупомянутых экспериментов с молекулярными пучками по проверке совпадения распределения Fр(E) с распределением Fm(E). Вопрос о возможности в реальных системах отличия Fр(E) от Fm(E) на такую малую величину остаётся открытым. В однородном поле 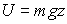 . Если m = 3× 10-26 кг (масса молекулы воды), g = 10 м/с2 (земное ускорение), z = 20 км, θo = 300 К (при этом
. Если m = 3× 10-26 кг (масса молекулы воды), g = 10 м/с2 (земное ускорение), z = 20 км, θo = 300 К (при этом 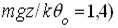 , то определяемая формулой (2.19) величина
, то определяемая формулой (2.19) величина  К, при этом градиент
К, при этом градиент  К/м, что намного (на четыре порядка) меньше градиента (2.16), который равен 0,014 К/м.
К/м, что намного (на четыре порядка) меньше градиента (2.16), который равен 0,014 К/м.


