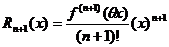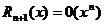Дифференциальные теоремы о среднем.
Если для всех точек x принадлежащих X выполняется неравенство f(x)<=f(x0) или f(x)=>f(x0), то говорят что функция f принимает в точке x0 наибольшее (наименьшее) значение на множестве X.
Теорема Ферма. Если функция определена в некоторой окрестности точки, принимает в этой точке наибольшее (наименьшее) значение и имеет конечную или определённого знака бесконечную производную, то эта производная равна 0.
Теорема Ролля, Лагранджа и Коши о средних значениях.
Теорема Ролля. Если функция f:
1) непрерывна на (a,b);
2) имеет в каждой точке интервала [a,b] конечного или определённого знака бесконечную производную;
3) принимает равные значения на концах (a,b) f(a)=f(b), то существует по крайней мере одна точка S принадлежащая [a,b] такая что f’(S)=0.
Теорема Лагранджа. Если функция f:
1) непрерывна на (a,b);
2) имеет в каждой точке интервала [a,b] конечного или определённого знака бесконечную производную;
3) то существует такая точка S принадлежащая [a,b] такая что f(b)-f(a)= f’(S)*(b-a) – формула приращений Лагранджа.
Следствие 1: Если функция непрерывна и имеет производную равную 0 во всех точках некоторого промежутка, то она на ней постоянна.
Следствие 2: Если функция непрерывна в некоторой окрестности точки и дифференцируема в проколотой окрестности этой же точки и существует конечный или бесконечный предел.
Теорема Коши. Если функция f и g:
1) непрерывна на (a,b);
2) дифференцируема в каждой точке интервала [a,b];
3) g’(x)<>0 для любого х принадлежащего (a,b), то существует такая точка S принадлежащая [a,b] такая, что (f(b)-f(a))/(g(b)-g(a))=f’(S)/g’(S).
Раскрытие неопределённости по правилу Лопиталя.
1. Неопределённость вида 0/0:
1) если функции f и g определы в окрестности x0, f(x0)=g(x0)=0 существуют конечные производные f’(x0)<>0 и g’(x0)<>0, то существует lim при x→x0 f(x)/g(x)= f’(x0)/g’(x0);
2) если:
а) функции f и g дифференцируемы на (a,b);
b) g’(x)<>0 для любого х принадлежащего (a,b);
с) lim при х→a f(x)=lim при х→a g(x)=0;
d) существует конечный или бесконечный предел lim при x→x0 (x0)/g’(x0), то существует предел lim при x→x0 f(x)/g(x), причём эти пределы равны.
2. Неопределённость вида ∞/∞:
а) функции f и g дифференцируемы на (a,b);
b) g’(x)<>0 для любого х принадлежащего (a,b);
с) lim при х→a f(x)=lim при х→a g(x)=∞;
d) существует конечный или бесконечный предел lim при x→x0 (x0)/g’(x0), то существует предел lim при x→x0 f(x)/g(x), причём эти пределы равны.
Признак монотонности функции.
Теорема. Если функция f(x) дифференцируема на (a,b) и f’(x)=>0 (f’(x)<=0) на (a,b), то функция не возрастает (не убывает) на (a,b).
Замечание. f’(x)>0 (f’(x)<0) на (a,b), то функция возрастает (убывает) на (a,b).
Отыскание точек локального экстремума.
Точка x0 называется точкой локального максимума (минимума) функции f(x), если для всех х из окрестности ∂ точки x0 выполняется неравенство f(x)<f(x0) (f(x)>f(x0)) при x<>x0.
Теорема (Необходимое условие локального экстремума). Если функция f(x) имеет в точке x0 локальный экстремум и дифференцируема в этой точке то f’(x0)=0.
Теорема (Достаточное условие локального экстремума). Если функция f(x) при переходе через точку x0 меняет свой знак с – на + то точка x0 – локальный минимум, а если с + на – то точка x0 – локальный максимум.
Направление выпуклости и точки перегиба графика.
Будем говорить что график функции y=f(x) имеет на (a,b) выпуклость направленную вниз (вверх), если он расположен, не ниже (не выше) любой касательной к графику функции на (a,b).
Теорема. Если функция y=f(x) имеет на (a,b) вторую производную и f’(x)=>0 (f(x)<=0), то во всех точках (a,b) график функции y=f(x) имеет выпуклость направленную вниз (вверх).
Точка M (x0,f(x0)) называется точкой перегиба графика функции y=f(x) если в точке M график имеет касательную и существует такая окрестность в точке x0 в пределах которой график функции y=f(x) слева и справа от точки x0 имеет разное направление выпуклости.
Теорема (Необходимое условие точки перегиба). Пусть график функции y=f(x) имеет перегиб в точке M (x0,f(x0)) и пусть функция y=f(x) имеет в точке x0 непрерывную вторую производную f’’(x) в точке x0 обращается в 0.
Теорема (Достаточное условие точки перегиба). Пусть функция y=f(x) имеет вторую производную в некоторой окрестности точки x0, тогда если в пределах указанной окрестности f’’(x) имеет разные знаки слева и справа точки x0, то график y=f(x) имеет перегиб в точке M (x0,f(x0)).
Асимптоты графика функций.
При исследовании поведения функции на бесконечности т.е. при х→+∞ и х→-∞ или в близи точек разрыва второго рода часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой, такие прямые называются асимптотами.
Существует 3-и вида асимптот: вертикальные, горизонтальные и наклонные
Опр.
Прямая х=х0 называется вертикальной асимптотой графика функции y=f(x), если хотя бы одно из предельных значений limх→х0+ f(x) limх→х0- f(x), равно +∞ или -∞.
Опр.
Прямая у=А называется горизонтальной асимптотой графика функции y=f(x), при х→+∞ или х→-∞, если limх→+∞ f(x) или limх→-∞ f(x) равняется А.
Опр.
Прямая у=kx+b (k неравно 0) называется наклонной асимптотой графика функции y=f(x), при х= +∞(-∞), если функцию f(x) можно представить в виде f=kx+в+α(x), α(x) →0, при х→+∞(х→-∞).
Формула Тейлора.
Теорема.
Пусть функция f(x) имеет в точке А и некоторой её окрестности производные порядка n+1, пусть х - некоторое значение аргумента из указанной окрестности х не равно А, тогда между точками х и А найдётся точка δ, такая, что справедлива следующая формула:
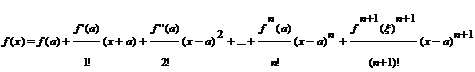
Формула Rn+1(x) = 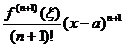 Называется формулой Тейлора, а выражение Rn+1(x) – остаточным членом в форме Лагранжа. Его можно переписать в другом виде т. к. точка δ принадлежащая (а,х), по найдётся такое число θ (тетта), 0< θ<1, что δ= а+ θ (х-а), и остаточный член примет вид: Rn+1(x) =
Называется формулой Тейлора, а выражение Rn+1(x) – остаточным членом в форме Лагранжа. Его можно переписать в другом виде т. к. точка δ принадлежащая (а,х), по найдётся такое число θ (тетта), 0< θ<1, что δ= а+ θ (х-а), и остаточный член примет вид: Rn+1(x) = 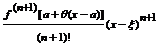
Формула Маклорена.
Формулой Маклорена называют формулу Тейлора (1), при а=0
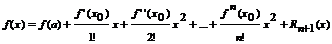 ; Остаточный член имеет вид:
; Остаточный член имеет вид:
1. В форме Логранжа.
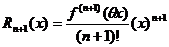
2. В форме Пиано.
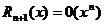
С помощью формулы Маклорена функцию можно с определённой степенью точности заменять многочленами, являющимися наиболее простыми элементарными функциями.
Неопределённый интеграл.
Если F(x) первообразная для функции f(x) на некотором промежутке Х, то множество функций F(x)+с, где с – произвольная постоянная, называется неопределённым интегралом от функции f(x) на этом промежутке и обозначается ∫f(x)dx=F(x)+c, где f(x) – под интегральная функция, f(x)dx – под интегральное выражение, х – переменная интегрирования.
Таблица основных интегралов.
1) ∫хаdx=(xa+1/a+1)+c;
2) ∫dx/x=ln(x)+c;
3) ∫dx/1+x2=arctg(x)+c;
4) ∫dx/√(1+x2)=arsin(x)+c;
5) ∫adx=ax/ln(a)+c;
6) ∫exdx=ex+c;
7) ∫sin(x)dx=-cos(x)+c;
8) ∫cos(х)dx=sin(x)+c;
9) ∫dx/cos(х)=tg(x)+c;
10) ∫dx/sin(x)=-ctg(x)+c;
11) ∫dx/(х2-a2)=1/2a*ln((x-a)/(x+a))+c;
12) ∫dx/√(х2-a2)=ln(x+√(x2+a))+c;
13) ∫dx/(х2+a2)=1/a*arctg(x/a)+c;
14) ∫dx/√(х2-a2)=arsin(x/a)+c;
Суммы Дарбу.
Пусть функция f(x) ограничена на отрезке. Разобьем ее на отрезки. Через M и m означим точную нижнюю грань и точную верхнюю грань. Суммы Mi∆xi и mi∆xi. Эти суммы называются соответственно нижней и верхней суммами. Сумма Дарбу имеет один геометрически смысл. Рассмотрим неотрицательную непрерывную функцию на отрезке и криволинейную трапецию, т е график функции ограниченными прямыми с координатами концов отрезка.
Формула Ньютона Лейбница.
Вычислять определенный интеграл как предел интегральной суммы очень трудно. Поэтому существует более удобный способ. Установлен, что функция непрерывна на отрезке интегрирования. Получаем формулу: Определенный интеграл равен разности интеграла от верхней грани и интеграла от нижней грани.
Замечание: Формула Ньютона Лейбница справедлива и для некоторых непрерывных функции.
Длина дуги кривой.
Пусть кривая задана уравнением y=f(x) и функция непрерывна на отрезке дифференцирования. Разобьем кривую на отрезки. Соединив соседние точки хордами получим ломанную длиной Р. Получаем формулу длины ломаной L=∫√1+f’f’dx
Ряд Маклорена.
f(x) = f(0)+ (f’(0)/1’)x + (f’’(0)/2’)x2 +(f’’’(0)/3’)x3 + (fn(0)/n’)xn
Данный ряд называется рядом Маклорена.
Следует отметить, что не все функции могут быть разложены в ряд маклорена, может оказаться, что ряд Маклорена, составленный формально для Функции f(x) является расходящимся либо сходящимся. Так же как и для числовых рядов сумму f(x) ряда Маклорена можно представить в виде: f(x)=Sn(x)+rn(x), где Sn n-ная частичная сумма рядов rn(x), n-ный остаток ряда, тогда на основании свойства сходящихся элементов можно сформулировать теорему:
Для того, что бы ряд Маклорена сходился к функции f(x) необходимо и достаточно что бы при n→∞ остатор ряда →0
limn→∞ rn(x)=0 для всех значений х из интервала сходимости ряда.
Замечание.
Ряд Маклорена является частным случаем ряда Тейлора.
Функции нескольких переменных. (Основные понятия).
Опр.
Пусть имеется n-переменных величин, и (х1,х2,…хn) из некоторого множества Х соответствует одно вполне определенное значение переменной величины z, тогда говорят, что задана функция нескольких переменных z=f(x1,x2,…xn) называется функцией нескольких переменных, а переменные x1,x2,…xn – независимыми переменными или аргументами z- зависимая переменная. Множество Х наз-ся областью определения функции.
Дифференциальные теоремы о среднем.
Если для всех точек x принадлежащих X выполняется неравенство f(x)<=f(x0) или f(x)=>f(x0), то говорят что функция f принимает в точке x0 наибольшее (наименьшее) значение на множестве X.
Теорема Ферма. Если функция определена в некоторой окрестности точки, принимает в этой точке наибольшее (наименьшее) значение и имеет конечную или определённого знака бесконечную производную, то эта производная равна 0.



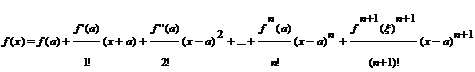
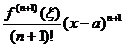 Называется формулой Тейлора, а выражение Rn+1(x) – остаточным членом в форме Лагранжа. Его можно переписать в другом виде т. к. точка δ принадлежащая (а,х), по найдётся такое число θ (тетта), 0< θ<1, что δ= а+ θ (х-а), и остаточный член примет вид: Rn+1(x) =
Называется формулой Тейлора, а выражение Rn+1(x) – остаточным членом в форме Лагранжа. Его можно переписать в другом виде т. к. точка δ принадлежащая (а,х), по найдётся такое число θ (тетта), 0< θ<1, что δ= а+ θ (х-а), и остаточный член примет вид: Rn+1(x) = 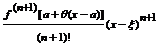
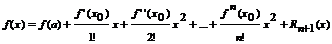 ; Остаточный член имеет вид:
; Остаточный член имеет вид: