Вопросы для изучения. Оценка значимости уравнения регрессии. Коэффициент ранговой корреляции Спирмена. Частная корреляция. Функции и коэффициенты эластичности.
Определения, формулы, справки
Оценить значимость регрессии - значит подтвердить или опровергнуть суждение о том, что, что наша модель соответствует наблюденным данным, а набор переменных достаточен.
А) Оценка значимости регрессии по критерию Фишера-Снедекора. Используем формулу:
| где:
| Q = å (yi - 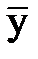 )2 )2
| - общая сумма квадратов отклонений yi от 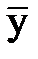 ; ;
|
|
| QR = å ( - - 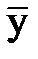 )2 )2
| - сумма квадратов отклонений  от от 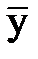 , обусловленная регрессией , обусловленная регрессией
|
|
| Qe = å (yi -  )2 )2
| - остаточная сумма квадратов ошибок - отклонений yi от  ; обусловлена влиянием неучтенных факторов. ; обусловлена влиянием неучтенных факторов.
|
Уравнение регрессии значимо на уровне вероятности a (a - вероятность ошибки 1-го рода: отвергнуть Н0, хотя она и верна), если выполняется неравенство:
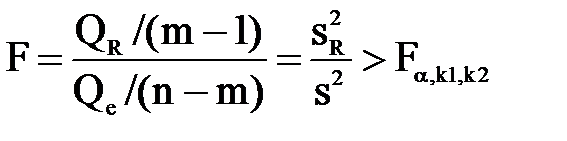 , ,
| (5.2)
|
где Fa,k1,k2 - табличное (критическое) значение F-критерия Фишера-Снедекора для уровня значимости a и степеней свободы k1 = m-1, k2 = n-m.
Статистика F показывает, во сколько раз объясненная регрессией дисперсия 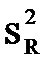 больше остаточной (необъясненной) дисперсии s2. Чем больше это отношение, тем более значима регрессия.
больше остаточной (необъясненной) дисперсии s2. Чем больше это отношение, тем более значима регрессия.
Для парной регрессии m=2 и критерий имеет вид:
уравнение значимо, если  . .
| (5.3)
|
Б) Оценка значимости парной регрессии по критерию Стьюдента. Значимость парной регрессии можно равносильно оценить по b1. Соответствующая нулевая гипотеза Но: b1 незначимо отличается от 0. Если она верна, то прямая регрессии параллельна оси ОХ: регрессия имеет вид  =b0, фактор Х ничего не объясняет. Обратная гипотеза Н1: b1 значимо отличается от 0; если это так, то уравнение регрессии значимо.
=b0, фактор Х ничего не объясняет. Обратная гипотеза Н1: b1 значимо отличается от 0; если это так, то уравнение регрессии значимо.
Критерий на основе статистики Стьюдента и гипотезы Н1:
Но: b1=0 отвергается, если t = ç 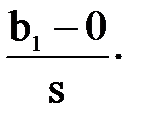  ç> t1-a,n-2. ç> t1-a,n-2.
| (5.4)
|
В) Оценка значимости регрессии по коэффициенту детерминации R2:
| R2 = QR/Q = 1 - Qe/Q.
| (5.5)
|
Известно, что 0£QR£Q. Отсюда диапазон изменения коэффициента детерминации: 0 £ R2 £ 1. R2 показывает долю вариации регрессионной переменной по отношению к общей вариации объясняемой переменной. Чем ближе R2 к 1, тем регрессионная модель более значима. Недостаток R2 – он растёт с ростом числа переменных р. Поэтому применяется скорректированный коэффициент детерминации 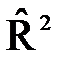 :
:
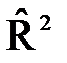 = = 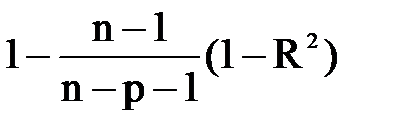 . .
| (5.6)
|
где р – число объясняющих переменных, с его ростом 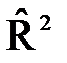 убывает.
убывает.
Г) Коэффициент ранговой корреляции Спирмена. Оценивает связь между атрибутивными переменными: качество жилищных условий, уровень образования, тестовые баллы, экзаменационные оценки. Для оценки объекты упорядочивают (ранжируют) по степени выраженности признаков переменных. Коэффициент ранговой корреляции Спирмена:
| 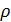 =1- 6 =1- 6 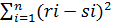 /(n3-n) /(n3-n)
| (5.7)
|
| где
| ri и si -
| ранги i-го объекта по переменным Х и Y,
|
|
| n -
| число пар наблюдений.
|
| | | | |
Если невозможно найти существенные различия между объектами, то им приписывают одинаковые средние ранги.
Д) Частные коэффициенты корреляцииоценивают связь между двумя переменными при исключении влияния остальных р-2 переменных:
ri-j,1,2,...,p =  ,i ,i  j, j,
|
(5.8)
|
где qii иqjj - алгебраические дополнения элементов rii и rjj матрицы коэффициентов корреляции.
Частный коэффициент корреляции принимает значения от -1 до +1. Для случая р=3 (матрицы симметричные):
 . .
|
(5.9)
|
Смысл частного коэффициента. Пусть имеется регрессия х1=bо+b1х2+b2х3+e. Оценим корреляцию между Х1 и Х2 при исключении влияния Х3. Найдем два уравнения регрессии: 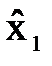 =bо+b1х3и
=bо+b1х3и  =
=  +
+  х3. Коэффициент корреляции между ошибками
х3. Коэффициент корреляции между ошибками  и
и  отражает тесноту частной корреляции между факторами Х1 и Х2.
отражает тесноту частной корреляции между факторами Х1 и Х2.
Е) Функции эластичности означает: на сколько процентов изменился 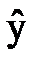 при изменении переменной хi ровно на 1%. Частная функция эластичности Еxi(
при изменении переменной хi ровно на 1%. Частная функция эластичности Еxi(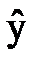 ) множественной регрессии
) множественной регрессии 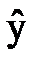 =f(x1,..., xр):
=f(x1,..., xр):
Еxi(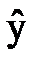 ) = ) = 
| (5.10)
|
Функция эластичности для парной регрессииy =bo + b1x+ e (см (1.2)):
5.2 Работа с тестами
1 Значение «m» в критерии Фишера-Снедекора для регрессии с р=2:
А 1, Б 2, В 3,Г 4
2 В двух случаях коэффициент детерминации тем больше, чем
А больше QR
Б больше Qe
В меньше Q
Г большеå (yi -  )2
)2
3 Критерий Стьюдента применим только для парной регрессии, поскольку:
А значимость b1 определяет значимость всей регрессии
Б коэффициент b1 стоит первым по порядку в регрессии
В коэффициент b1 имеет наибольшее значение в регрессии
Г коэффициенты b2, b3.. не влияют на значимость регрессии
4 Доля вариации переменной 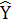 по отношению к общей вариации Y есть:
по отношению к общей вариации Y есть:
А статистика Фишера F
Б статистика Стьюдента t
В дисперсия зависимой переменной Y
Г коэффициент детерминации R2
5 Значение переменных заменяют их рангами, поскольку:
А переменные являются количественными
Б переменные являются атрибутивными (качественными)
В сравнение рангов предпочтительнее сравнения количественных значений
Г зачастую точность измерения переменныхнедостаточна
6 Уравнение асимптоты для функции эластичности E= b1x/(bo +b1x)
А Е=bo; Б Е=b1; В Е=1; Г Е=2
7E= b1x/(bo +b1x)– это функция эластичности для парной регрессии вида:
А квадратичная
Б гипербола
В линейная
Г парабола
5.3 Решение задач и контрольные вопросы
Задача1. Проверить уравнение регрессии на значимость по критерию Фишера-Снедекора (5.2). Исходные данные: QR=17, Qe=6, m=3, n=10, α=0,05, k1=m-1, k2=n-m.
Задача 2. Проверить парное уравнение регрессии на значимость по критериюСтьюдента (5.4). Исходные данные: b1=2,50, s=1,5, X=4, 6, 7, 2; α=0,05.
Задача 3. Построить график зависимости скорректированного коэффициента детерминации 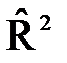 =
= 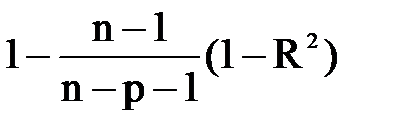 от числа переменных в регрессии при n=7, R2 =0,85 и р=1, 2, 3, 4. Сделать вывод.
от числа переменных в регрессии при n=7, R2 =0,85 и р=1, 2, 3, 4. Сделать вывод.
Задача 4. Кадровая служба изучает связь между эффективностью работника (шкала от 1 до 5) и образованием. Составлена таблица, проставлены ранги (выделены жирно):
| ФИО
| Образование
| Эффективность
| Разность рангов
| Квадрат разности
|
| Признак
| Ранг
| Признак
| Ранг
|
| А
| Магистр
| (1+2)/2=1.5
| 5
| 1
| -0.5
| 0.25
|
| Б
| Спец-ст
| (5+6)/2=5.5
| 2
| 5
| -0.5
| 0.25
|
| В
| Спец-ст
| 3
| 4
| 2
| -1
| 1
|
| Г
| Магистр
| (1+2)/2=1.5
| 3
| (3+4)/2=3.5
| 2
| 4
|
| Д
| Спец-ст
| (5+6)/2=5.5
| 1
| 6
| 1.5
| 2.25
|
| Е
| Бакалавр
| 4
| 3
| (3+4)/2=3.5
| -0.5
| 0.25
|
1).Объяснить содержание таблицы, 2) Вычислить коэффициент ранговой корреляции Спирмена, 3) Сделать вывод.
Задача 5. Записать выражение (5.8) для случая трех факторных переменных (р=3) и частного коэффициента корреляции r1-2,3 и вычислить его значение на основе корреляционной матрицы (5.9). Выполнить анализ решения задачи:
Решение. Построим алгебраические дополнения на основе матрицы (5.9), а затем и само это выражение (i=1, j=2, k=3):
| | q11=+(1- 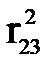 )=0,75 )=0,75
| q22=+(1- 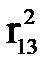 )=0,64 )=0,64
| q12= -(r12- r13 r23)=-0,40
| |
|  . .
| (5.12)
|
| | | | | | |
Ответ: частный коэффициент корреляция между х1 и х2 при исключении влияния х3: r1-2,3=0,58, т.е. достаточно существенен.
Задача 6. Для условий задачи 5 и значений: r12=0,6; r13= r23=0,8 вычислить частный коэффициент корреляции r1-2,3.
Ответ: r1-2,.3=-0,11.
Задача 7. Дано: линейное уравнение регрессии 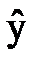 =5+6x1-2x2, выборочные средние:
=5+6x1-2x2, выборочные средние: 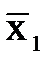 =10,
=10,  =20,
=20, 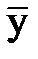 =25. Найти частную функцию эластичности по переменной х2. Выполнить анализ алгоритма решения задачи:
=25. Найти частную функцию эластичности по переменной х2. Выполнить анализ алгоритма решения задачи:
1) По формуле (5.10) искомая функция: Еx2(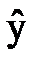 ) = (¶
) = (¶ 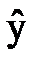 /¶x2)(x2/
/¶x2)(x2/ 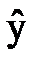 )= -2x2/(5+6x1--2x2).
)= -2x2/(5+6x1--2x2).
2) Положим 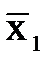 =10 и получим частную функцию эластичности Е(x2)= -2x2/(65-2x2).
=10 и получим частную функцию эластичности Е(x2)= -2x2/(65-2x2).
3) Для  =20 получим средний частный коэффициент эластичности
=20 получим средний частный коэффициент эластичности 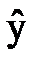 по x2:
по x2:  =
= 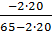 = -1,60.
= -1,60.
Вывод: в окрестности выборочных средних увеличение x2 на 1% приводит к уменьшению 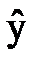 на 1,60%.
на 1,60%.
Задача 8. Дано парное уравнение регрессии со степенной функцией: 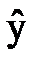 =5×х1/2. Найти функцию и средний коэффициент эластичности. Выполнить анализ решения задачи.
=5×х1/2. Найти функцию и средний коэффициент эластичности. Выполнить анализ решения задачи.
Решение. На основе (5.10):
Еx(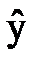 )=
)=  =
=  = 0,5.
= 0,5.
Ответ: функция эластичности для степенной функции есть константа.
Контрольные вопросы:
1) Как оценивается значимость регрессии по критерию Фишера-Снедекора
2) То же - по критерию Стьюдента
3) То же - по коэффициенту детерминации
4) Чем скорректированный коэффициент детерминации лучше, чем простой
5) Почему экономистов привлекает коэффициент эластичности
5.4 Решение сквозной задачи №1: Построение и исследование модели магазина - линейной парной регрессии (п.п. 12-17)
12) Найдём 95%-й доверительный интервал для среднего прогнозного значения объема продаж, т.е для Мх=11(Y). Ранее мы нашли точечную оценкудля МО Мх=11(Y), она равна 17,37.
Рассчитаем дисперсию и СКО ошибок ei(см. таблицу3.5 графы 1, 6, 8):
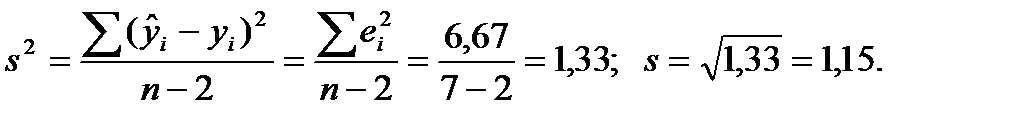
Искомая дисперсия и СКО СВ  х=11:
х=11:


Для расчёта интервала используем СВ t, 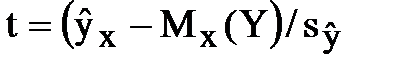 , которая имеет закон распределена Стьюдента. Соответствующее число степеней свободы распределения k = n–2 = 7–2=5. По таблице В.1 (см приложение В) находим критическое значение статистики Стьюдента: t0,95;5=2,57. Искомый 95%-й (α=5%) доверительный интервал для среднего прогнозного значения объема продаж магазина "Рыба-8" в общем виде:
, которая имеет закон распределена Стьюдента. Соответствующее число степеней свободы распределения k = n–2 = 7–2=5. По таблице В.1 (см приложение В) находим критическое значение статистики Стьюдента: t0,95;5=2,57. Искомый 95%-й (α=5%) доверительный интервал для среднего прогнозного значения объема продаж магазина "Рыба-8" в общем виде:
 х-D£М(Y)х£
х-D£М(Y)х£  х+D,
х+D,
где D= 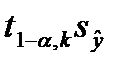 =2,57×1,48=3,80 (при х=11).
=2,57×1,48=3,80 (при х=11).
Нижнее значение интервала:  D= 17,37-3,80=13,57.
D= 17,37-3,80=13,57.
Верхнее значение интервала: 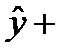 D= 17,37+3,80=21,17.
D= 17,37+3,80=21,17.
Окончательно, интервал имеет вид:13,57£М(Y)х=11 £ 21,17.
Вывод: прогнозный доверительный интервал велик (21.17-13.57=7.60), поэтому и риски открытия нового магазина велики.
13) Найдём с доверительной вероятностью 0,95 (α=0,05) интервальные оценки для неизвестного нам коэффициента регрессии b1. Формула для расчета интервала:b1-D£b1£b1+D,
где 
Нижнее значение интервала: 1,54-0,48=1,06.
Верхнее значение интервала: 1,54+0,48=2,02.
Окончательно, интервал имеет вид:1,06 £b1£ 2,02.
14) Качество уравнения можно определить по остаточной дисперсии (дисперсии остатков или - ошибок). Для этого рассчитаем с доверительной вероятностью 0,95 её интервальные оценки. Найдем по таблице Г.1 (см приложение Г) критические значения статистик хи-квадрат:


Формула для доверительного интервала и расчёт по ней:
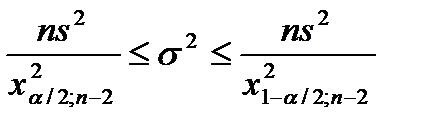
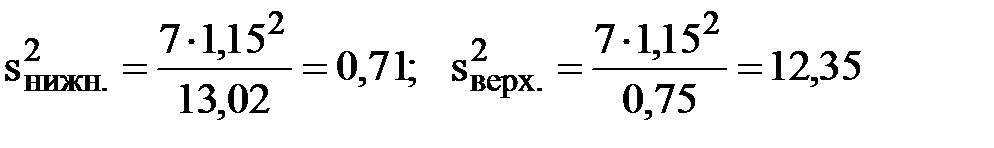

15) Оценим с доверительной вероятностью 0,95 значимость уравнения регрессии по критерию Фишера. Для этого вычислим три суммы квадратов и значение СВ F:
| Общая сумма:
| Q=å(yi-  )2=13,77+7,35+2,93+0,51+0,51+1,67+68,73= 95,47 )2=13,77+7,35+2,93+0,51+0,51+1,67+68,73= 95,47
|
| Регрессионная сумма:
| QR=å( i- i-  )2=13,99+13,99+4,84+0,44+0,78+8,56+49,56=
=89,44 )2=13,99+13,99+4,84+0,44+0,78+8,56+49,56=
=89,44
|
| Остаточная сумма
| Qe=å( i-у)2=6,67 (см. таблицу 2.2). i-у)2=6,67 (см. таблицу 2.2).
|
| Значение статистики Фишера:
| 
|
Уравнение регрессии значимо, если СВ F>Fa,k1,k2, где степени свободы k1=m-1=2-1=1, k2=n-m=7-2=5. По таблице Д.1 (см приложение Д) находим критическое значение статистики F0,05;1;5=6,61. Так как 67,63> 6,61, то делаем вывод: уравнение значимо, коэффициент регрессии b1=1,54 значимо отличается от нуля (отвергаем нулевую гипотезу).
16) Оценим на уровне a=0,05 значимость уравнения регрессии по критерию Стьюдента: уравнение регрессии значимо, еслиt>tкрит. Значение статистики Стьюдента в нашем случае:
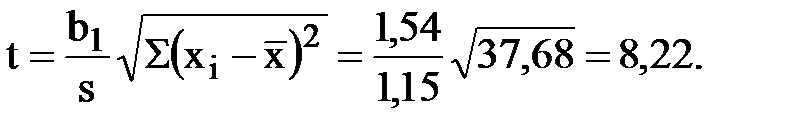
По таблице В.1 находим tкрит.=t0,95;7-2=5=2,57. Так как 8,22 > 2,57, то нулевую гипотезу Но(Но : β1=0) отвергаем и принимаем противоположную гипотезу Н1: уравнение значимо.
17) Последнее исследование нашего уравнения. Оно также связано с оценкой его значимости –через коэффициент детерминации R2(детерминировать – делать предопределённым, снижать неопределённость). Используем формулу (см п.15): R2= QR/Q = 89,44/ 95,47 = 0,94. Это очень высокое значение, поскольку 0  R2
R2  1. Смысл коэффициента детерминации: R2 показывает, какая доля вариации зависимой переменной Yобусловлена вариацией фактора X. Ответ: эта доля составляет 94%.
1. Смысл коэффициента детерминации: R2 показывает, какая доля вариации зависимой переменной Yобусловлена вариацией фактора X. Ответ: эта доля составляет 94%.
(Конец решения сквозной задачи №1).



 )2
)2
 -
-  )2
)2
 )2
)2
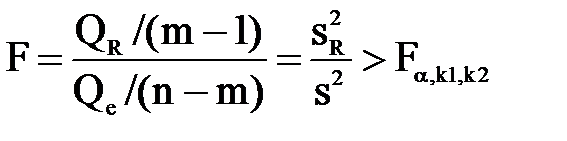 ,
,
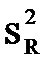 больше остаточной (необъясненной) дисперсии s2. Чем больше это отношение, тем более значима регрессия.
больше остаточной (необъясненной) дисперсии s2. Чем больше это отношение, тем более значима регрессия. .
.
 =b0, фактор Х ничего не объясняет. Обратная гипотеза Н1: b1 значимо отличается от 0; если это так, то уравнение регрессии значимо.
=b0, фактор Х ничего не объясняет. Обратная гипотеза Н1: b1 значимо отличается от 0; если это так, то уравнение регрессии значимо.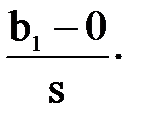
 ç> t1-a,n-2.
ç> t1-a,n-2.
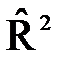 :
: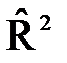 =
= 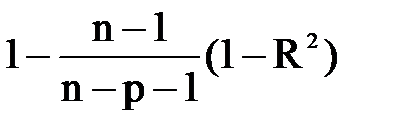 .
.
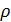 =1- 6
=1- 6 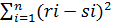 /(n3-n)
/(n3-n) ,i
,i  j,
j,
 .
.
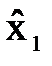 =bо+b1х3и
=bо+b1х3и  =
=  +
+  х3. Коэффициент корреляции между ошибками
х3. Коэффициент корреляции между ошибками  и
и  отражает тесноту частной корреляции между факторами Х1 и Х2.
отражает тесноту частной корреляции между факторами Х1 и Х2.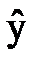 при изменении переменной хi ровно на 1%. Частная функция эластичности Еxi(
при изменении переменной хi ровно на 1%. Частная функция эластичности Еxi(
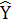 по отношению к общей вариации Y есть:
по отношению к общей вариации Y есть: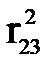 )=0,75
)=0,75
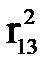 )=0,64
)=0,64
 .
.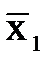 =10,
=10,  =20,
=20,  =
= 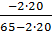 = -1,60.
= -1,60. =
=  = 0,5.
= 0,5.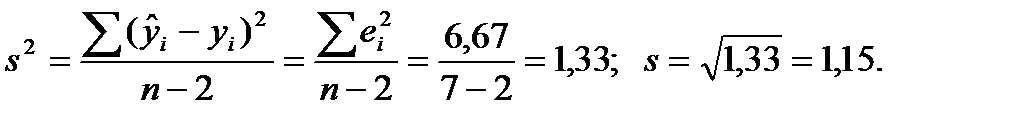
 х=11:
х=11:

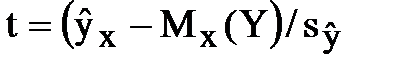 , которая имеет закон распределена Стьюдента. Соответствующее число степеней свободы распределения k = n–2 = 7–2=5. По таблице В.1 (см приложение В) находим критическое значение статистики Стьюдента: t0,95;5=2,57. Искомый 95%-й (α=5%) доверительный интервал для среднего прогнозного значения объема продаж магазина "Рыба-8" в общем виде:
, которая имеет закон распределена Стьюдента. Соответствующее число степеней свободы распределения k = n–2 = 7–2=5. По таблице В.1 (см приложение В) находим критическое значение статистики Стьюдента: t0,95;5=2,57. Искомый 95%-й (α=5%) доверительный интервал для среднего прогнозного значения объема продаж магазина "Рыба-8" в общем виде: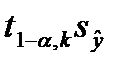 =2,57×1,48=3,80 (при х=11).
=2,57×1,48=3,80 (при х=11). D= 17,37-3,80=13,57.
D= 17,37-3,80=13,57. D= 17,37+3,80=21,17.
D= 17,37+3,80=21,17.


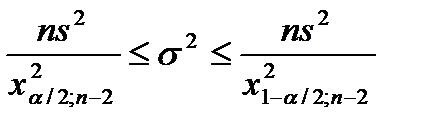
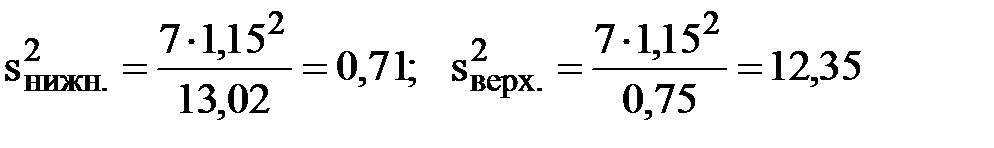

 )2=13,77+7,35+2,93+0,51+0,51+1,67+68,73= 95,47
)2=13,77+7,35+2,93+0,51+0,51+1,67+68,73= 95,47
 i-
i- 
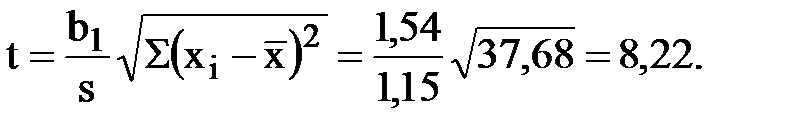
 R2
R2 


