Если представляет собой непрерывную случ. вел-ну и если количество k>10, то в этом случае для представления рез-тов исп-ется интервальный ряд распред-я.
V - число интервалов, приблизительно от 7 ло 11.
Ф-ла Стерджеса: R=max xi - min xi (R -размах)
h=R/V, где,h - шаг.
xk-1-h<xk<=max xi
Билет 27
Понятие временного ряда. Линейные, нелинейные тренды.
yt=f(xt,t)+εt
xt-детерминированный фактор, εt-случ. вел-на мат.ожидания, к-рая равна 0.
Анализ временных рядов с целью прогнозирования поведения yt (объем производства, прибыль). На эти временые показатели влияют случ. факторы, к-рые не поддаются точному анализу.
Линейный тренд. Если временной ряд имеет вид регрессивной зависимости: yt=α0 +Σki=1 αiφi(t) + εt, то он представляет собой тренд.
Если εi(t) нелинейная ф-я, то тренд нелинейный, а если линейная, то линейный.
===========================================================
Билет№28
(1) Условная вер-ть. Теорема умнож-я вер-тей.
Произведением двух соб-й А и В наз. соб-е АВ, состоящее в совместном появлении этих соб-й (А-деталь годная, В-деталь окрашенная, АВ- годная и окрашенная). Произ-ем неск. соб-й наз. соб-е состоящее в совместном появлении всех этих соб-й. Во введении случайное соб-е определено как соб-е, к-рое при осуществлении совок-ти услови й S может произойти или не произойти. Если при вычислении в-ти соб-я никаких др. ограничений, кроме условий S, не налагается, то такую в-ть наз. безусловной; если же налагаются и др. дополнительные условия, то в-ть соб-я наз. условной. Напр, часто вычисляют в-ть собы-я В при дополнительном условии, что произошло соб-е А. Заметим, что и безусловная в-ть, строго говоря, явл. условной, поскольку предполагается осуществление условий S. Условной в-тью Ра(В) наз. в-ть соб-я В, вычисленную в Предположении, что соб-е А наступило: Ра(в)=Р(АВ)/Р(А) (Р(А)>0). Рассм-м два соб-я А и В, пусть вер-ти Р(А) и Ра(В) известны. Как найти совмещение этих соб-й,т.е. вер-ть того что появится и соб-е А и соб-е В. Ответ на этот вопрос дает теорема умнож-я: вер-ть совместного появл-я двух соб-й равна произведению в-ти одного из них на условную вер-ть другого, вычисленную в предположении, что первое соб-е уже наступило Р(АВ)=Р(А)*Ра(В). Д-во: по определению условной вер-ти Ра(В)=Р(АВ)/Р(А), отсюда Р(АВ)=Р(А)*Ра(В). Следствие: вер-ть совместного появл-я неск. соб-й равна произведению в-ти одного из них на условные в-ти всех остальных, причем вер-ть каждого последующего соб-я вычисляется в предположении, что все предыдущие соб-я уже появились
Где______________________ вер-ть соб-я ______. Вычисленная в предположении, что соб-я ___________________ наступили. В частности, для трех соб-й___________________________________ (порядок может быть выбран любой, безразлично какое соб-е считать перв., вторым).
==========================================================
Билет№23
(1) Ф-я Лапласа, ее св-ва. Вер-ть попадания в интервал для норм. распред-я с.в. Правило 3 сигм.
Если случ. Вел-на Х задана плот-тью распред-я ____, то вер-ть того, что Х примет знач-е, принадлежащее интервалу ________, такова:
Пусть случ. Вел-на Х распределена по нормальному закону. Тогда вер-ть того, что Х примет знач-е, принадлежащее интервалу __________, равна
Преобразуем эту ф-лу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную _____________. Отсюда ______________________________. Найдем новые пределы интегрирования. Если ______, то ____________; если ______ то_____________. Таким образом, имеем
Пользуясь ф-цией Лапласа (Теорема: раз в-ть того, что в n независ. исп-ях в кажд. из к-рых в-ть появл-я соб-я А равно р, причем 1>р>0, то соб-е А наступит не менее m1 раз и не более m2 раза приблизительно равно

При решении задач, требующих применения инт. Теоремы, пользуются спец. Таблицами, так как неопред. интеграл ___________ не выражается ч-з элементарные ф-ции. В ней даны знач-я ф-ции _______ для положит. Знач-й х и для х=0, для х<0 пользуются той же табл.й (т.к. ф-я ______ нечетка). Ф-цию _______ часто наз. Ф-ей Лапласа. Вер-ть того, что соб-е А появится в n исп-ях от к1 до к2 раз:
Окончательно получим
Правило 3-х сигм: преобразуем ф-лу
Положив ____________. В итоге получим
Если _________ и, =>, _____________, то
Т.е. вер-ть того, что отклонение по абсолютной вел-не будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Др. словами, в-ть того, что абсолютная вел-на отклонения превысит утроенное ср. квадратическое отклонение, оч. мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие соб-я исходя из принципа невозможности маловероятных соб-й можно считать практически невозм.. В этом и состоит сущность правила трех сигм: если случ. вел-на распределена нормально, то абсолютная вел-на ее отклонения от математического ожидания не превосходит утроенного среднего квад-ратического отклонения. На практике правило трех сигм применяют так: если распред-е изучаемой случ. вел-ны неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая вел-на распределена нормально; в противном случае она не распределена нормально.
F(х;у).
(2) Двумерная ф-я распред-я и ее св-ва. (стр. 158 +гр-к)Рассм-м двумерную случ. Вел-ну (Х: У) (безразлично, дискрутную или непрерывную). Пусть х, у – пара действительных чисел. Вер-ть соб-я, состоящего в том, что Х примет знач-е, меньшее х, и при этом У примет знач-е, меньшее у, обозначим ч-з F(х;у). Если х и у будут изменяться, то, вообще говоря, будет изменяться и F(х;у), т.е. F(х;у) есть ф-я от х и у. Ф-цией распред-я двумерной случ. вел-ны (Х; У) наз. ф-цию F(х;у), определяющую для каждой пары чисел х, у вер-ть того, что Х примет знач-е, меньшее х, и при этом У примет знач-е, меньшее у: F(х;у)=Р (Х< х, У <у). Геом-ки это рав-во можно истолковать так: F(х;у) есть вер-ть того, что случ. точка (Х; У) попадет в бесконечный квадрант с вершиной (х,у), расположенный левее и ниже этой вершины. Св-во1: знач-е ф-и распред-я удовлетворяют двойному нер-ву ______________________. Д-во: св-во вытекает из опред-я ф-ции распред-я как вер-ти: вер-ть – всегда неотрицат. Число. Не превышающее единицу. Св-во2: F(х;у) есть неубывающая ф-я по кажд.у аргументу, т.е.
Св-во3: имеют место предельные соотн-ниея
Св-во4: а) при у=_____ ф-я распред-я системы становится ф-цией распред-я составляющей Х:_____________________. Б) при х=_____ ф-я распред-я системы становится ф-ей распред-я составляющей У:
_______________________.
============================================================
Билет№ 24
(1)Нерав-во Чебышева. (стр. 102)
Нерав-во Ч. справедливо для дискр. И непрер. случ. Вел-н. Рассм-м диск. Случ. В-ну Х. Заданную табл.й распред-я:
Поставим перед собой задачу оценить вер-ть того, что отклонение случ. Вел-ны от ее МО не превышает по абсолютной вел-не полож. Числа _____. Если _____ достаточно мало, то мы оценим. Таким образом, вер-ть того, что Х примет знач-я, достаточно близкие к своему мат. Ожиданию. Ч. доказал нерав-во, позволяющее дать интересующую нас оценку. Неравен-во Ч.: вер-ть того, чт отклонение случ. Вел-ны Х от ее МО по абсолютной вел-не меньше полож. Числа _____, не меньше чем _____________________:
Д-во: так как соб-я, состоящие в осуществлении неравенств ____________________________, противоположны, то сумма их в-тей равна ед-це, т.е.
Отсюда интересующая нас вер-ть
Т.о., задача сводится к вычислению вер-ти __________________________. Напишем выражение дисперсии случ. Вел-ны Х:
Очевидно, все слагаемые этой суммы неотрицательны. Отбросим те слагаемые, у к-рых ___________________________(для оставшихся слагаемых ___________________________), вследствие чего сумма может только уменьшиться. Условимся считать для опред.сти, что отброшено k перв. слагаемых (не нарушая общности, можно считать, что в табл. распред-я возм. знач-я занумерованы именно в таком порядке). Таким образом,
Заметим, что обе части нерав-ва ______________________________________________ положительны, поэтому. Возведя их в квадрат, получим равносильное нерав-во _________________________. Воспользуемся этим замечанием и, заменяя в оставшейся сумме каждый из множителей___________________ числом _________ (при этом нерав-во может лишь усилиться), получим
По теореме слож-я, сумма вер-тей ________________________ есть вер-ть того, что Х примет одно, безразлично какое, из знач-й __________________________, а при любом из них отклонение удовлетворяет нер-ву ________________________. Отсюда следует, что сумма ______________________ выражает вер-ть
Это соображение позволяет переписать нерав-во (**) так:
Или
Подставляя (***) в (*), окончательно получим
Ч.т.д.
2. Точечн. оценка числ. хар-к. Осн. опред-я. Метод моментов.
Точечной наз. оценку, к-рая определяется одним числом.
Оценка генер. дисперсии по исправленной выборочной.
Пусть из генер. совок-ти в рез-те n независ. наблюдений над количественным признаком X извлечена повторная выборка объема n:
знач-я признака х1х2 хк
частоты n1n2 nк
При этом n1+n2+ +nk=n
Требуется по данным выборки оценить неизвестную генеральную дисперсию Dr. Если в кач. оценки генер. дисперсии принять выбоочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное знач-е генер. дисперсии. Объясняется это тем, что, как можно доказать, выборочная дисперсия явл. смещенной оценкой Dr, др. словами, мат.ожидание выборочной дисперсии не равно оцениваемой генер. дисперсии, а равно
M[Dв]=((n-1)/n)Dr
Получим исправленную дисперсию, которую обычно обозначают ч-з s2
см.стр.212
Исправленная дисперсия явл., конечно, несмещенной оценкой генер. дисперсии. Действительно
Итак, в кач. оценки генер. дисперсии принимают исправленную дисперсию
Для оценки же среднего квадратического отклонения генер. совок-ти исп-ют “исправленное” ср. квадратическое отклонение, к-рое равно квадратному корню из исправленной дисперсии:
Подчеркнем, что s не явл. несмещенной оценкой; чтобы отразить этот факт, мы будем писать так: “исправленное” ср. квадратичное отклонение.
Метод моментов.
Метод моментов, предложенный Пирсоном основан на том, что начальные и центральные эмперические моменты являются состоятельными оценками соответственно начальных и центральных теоретических моментов того же порядка. Достоинство метода - сравнительная его простота. Метод моментов точечной оценки неизвестных парам-ров заданного распред-я состоит в приравнивании теоретических моментов рассматриваемого распред-я соответствующим эмпирическим моментам того же порядка.
А.Оценка одного парам-ра: для оценки одного парам-ра достаточно иметь олно ур-е относительно этого парам-ра. Следуя методу моментов, приравняем, напр, начальный теоретический момент перв. порядка к начальному эмпирическому моменту перв. порядка:
стр.227
(1)
МО М(Х), как видно из соотн-ниея
есть ф-я от ,поэтому (1) можно рассм-ть как ур-е с одним неизвестным . Решив это ур-е относительно праметра , тем самым найдем нго точесную оценку 1, к-рая явл. ф-цией от выборочной ср., => и от вариант выборки:
Б.Оценка 2-х парам-ров: для отыскания 2-х парам-ров необходимы 2 ур-я относительно этих парам-ров
=========================================================
Билет 29. 1.Интервальная оценка числ. хар-к. Доверительный интервал. Осн. опред-я. Точечной наз. оценку, к-рая определяется одним числом. При выборке малого объема точечн. оценка может значительно отличаться от оцениваемого парам-ра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.Интервальной наз. оценку, к-рая определяется 2-мя числами - концами интервала. Интервальные оценки позволяют установить точ-ть и надеж-ть оценок.
Пусть найденная по данным выборки статистическая хар-ка служит оценкой неизвестного парам-ра .Будем считать постоянным числом. Если >0 и < , то чем меньше , тем оценка точнее. Таким образом, полож. число хар-ет точ-ть оценки.
Однако статистические методы не позволяют категорически утверждать, что оценка удовлетворяет нер-ву ; можно лишь говорить о в-ти , с к-рой это рав-во осущ-ся.
Надеж-тью (доверительной в-тью) оценки по наз. в-ть , с к-рой осущ-ся нерав-во . Обычно надеж-ть оценки задается наперед, причем в кач. берут число, близкое к ед-це.Наиб. часто задают надеж-ть равную 0.95; 0.99; 0.999.
Пусть в-ть того, что равна :
см.стр213
Заменив нерав-во равносильным ему двойным нерав-вом или имеем
Это соотн-ниее следует понимать так: в-ть того, что интервал заключает в себе неизвестный парам-р , равна .
Доверительным интервалом наз. интервал , к-рый покрывает неизвестный парам-р с заданной надеж-тью . От выборки к выборке будут меняться концы доверительного интервала, т.е. доверительные границы сами являются случайными вел-нами.
2. Система случ. вел-н. Корреляционный момент и коэффициент корреляции, их свойства.
Для описания системы двух случ. вел-н кроме мат.ожиданий и дисперсий составляющих исп-ют и др. хар-ки; к их числу относятся корреляционный момент и коэффициент корреляции. Корреляционным моментом μ xy случ. вел-н X и Y наз. матем. ожидание произведения отклонений этих вел-н: μxy = М{[X-M(X)][Y-M(Y)]}
Для вычисления корреляционного момента дискр. вел-н исп-ют ф-лу
См. стр.176
А для непрер. вел-н – ф-лу
См стр. 176.
Корреляционный момент служит для хар-ки связи между вел-нами X и Y. Корреляционный момент будет равен нулю, если X и Y независимы; =>, если корреляционный момент не равен нулю, то X и Y – зависимые случ. вел-ны.
Теорема 1. Корреляционный момент двух независ. случ. вел-н X и Y равен нулю. Доказательство: т.к. X и Y – независимые случ. вел-ны, то их отклонения X-M(X) и Y-M(Y) также независимы. Пользуясь свойствами мат.ожидания (мат.ожидание произведения независ. случ. вел-н равно произведению мат.ожиданий сомножителей) и отклонения (мат.ожидание отклонения равно 0), получимμxy =M{[X-M(X)][Y-M(Y)]}=M[X-M(X)]M[Y-M(Y)]=0
Из опред-я корреляционного момента следует, что он имеет размерность, равную произведению размерностей вел-н X и Y. Такая особ-ность корреляционного момента явл. недостатком этой числовой хар-ки, поскольку сравнение корреляционных моментов различных систем случ. вел-н становится затруднительным. Для того, чтобы устранить этот недостаток, вводят новую числовую хар-ку – коэффициент корреляции.
Коэффициентом корреляции rху случ. вел-н X и Y наз. отн-ниее корреляционного момента к произведению средних квадратических отклонений этих вел-н: см. стр. 178
Так как размерность μxy равна произведению размерностей вел-н X и Y, σх имеет размерность вел-ны Х, σу имеет размерность вел-ны У, то rху - безразмерная вел-на. Таким образом, вел-на коэффициента корреляции не зависит от выбора единиц измерения случ. вел-н. В этом состоит преимущество коэффициента корреляции перед корреляционным моментом.
Очевидно, коэффициент корреляции независ. случ. вел-н равен 0 (так как μxy=0)
Теорема 2. Абсолютная вел-на корреляционного момента двух случ. вел-н X и Y не превышает среднего геометрического их дисперсий: │ μxy │≤ √DхDу.
Доказательство: Введем в рассмотрение случ. вел-ну Z1=σуX-σхY и найдем ее дисперсию D(Z1)=M[Z1-mZ1]2. Выполнив выкладки, получим
D(Z1)=см.стр.178
Любая дисперсия неотрицательна, поэтому см.стр.179
Отсюда μxy≤σхσу (2)
Введя случ. вел-ну Z2=σуX+σхY, аналогично найдем μxy≥-σхσу (3)
Объединим (2) и (3): -σхσу ≤ μxy ≤ σхσу или │ μxy│≤ σхσу (4)
Итак, │ μxy │≤ √DхDу
Теорема 3:Абсолютная вел-на коэффициента корреляции не превышает единицы:
│ rху│≤ 1
Доказательство: Разделим обе части двойного нерав-ва (4) на произведение положительных чисел σхσу: -1≤ rху≤1
Итак, │ rху│≤1
==================================================
Билет№25
(1)Теоремы Чебышева и Бернулли.
Теорема Чебышева дает одну из наиб. возм. форм закона больших чисел. Она устанавливает связь между средним арифметическим и ее математическим ожиданием наблюденных знач-й случ. вел-ны.
Yn=(X1 + X2 + …. + Xn) * 1/n = 1/n 
M[Yn] = i/n  = 1/n *
= 1/n *  = 1/n * n * mx = mx
= 1/n * n * mx = mx

Мат ожидание среднего не зависит от n
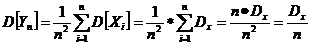

Теорема Чебышева устанавливает в точной количественной форме это свойство устойчивости среднего арифметического.
Теорема Чебышева: При достаточно большом числе независ. опытов ср. арифметическое наблюденных знач-й случ. вел-ны сходится по в-ти n т ее математическому ожиданию.В математической форме это означает следующее:
| 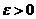 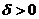 близко к 0 близко к 0
|
 , где
, где  и
и 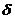 сколь угодно положительные числа
сколь угодно положительные числа 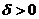 и
и 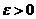 .
.
Теорема Бернулли: При неограниченном увеличении числа опытов n, частота соб-я a сходится по в-ти к его в-ти P
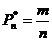 - (в-ть). m-произошло соб-е. n-число опытов.
- (в-ть). m-произошло соб-е. n-число опытов.

Теор. Бернулли: если в кажд. из n независ. исп-й вер-ть р появл-я соб-я А постоянна, то как угодно близка к ед-це вер-ть того, что отклонение отн-ной частоты от вер-ти р по абсолютной вел-не будет сколь угодно малым, если число исп-й достаточно велико. Др. словами, если ___сколь угодно малое положит. Число. То при соблюдении условий теоремы имеет место рав-во
2.Проверка гипотез, ошибки 1-го и 2-го рода. Мощ-ть критерия.
Часто необх-мо знать закон распред-я генер. совок-ти. Если закон распред-я неиз-вестен, но имеются основания предположить, что он имеет опред. вид (назовем его А), выдвигают г-зу: ген.совок-ть распределена по закону А. Таким образом, в этой г-зе речь идет о виде предполагаемого распред-я.Возможен случай, когда закон распред-я известен, а его парам-ры неизвестны. Если есть основания предположить, что неизвестный парам-р @ равен опред.му знач-ю @0, то выдвигают г-зу: @=@0. Таким образом, в этой г-зе речь идет о предполагаемой вел-не парам-ра одного известного распред-я. Стат. наз. г-зу о виде неизвестного распред-я, или о парам-рах известных распред-й. Нулев. (основной) наз. выдвинутую г-зу Н0. Конкурирующей (альтернативной) – г-зу Н1, к-рая прот-чит нулев.. Простая - содержащая только одно предположение. Сложная – состоит из конечного или бесконечного числа простых гипотез. Критич. обл-тью наз. совок-ть знач-й критерия, при к-рых нулевуюг-зу отвергают. Обл-тью принятия г-зы (обл-тью допустимых знач-й) наз. совок-ть знач-й критерия, при к-рых г-зу принимают. Основной принцип проверки стат. гипотез можно сформулировать так: если наблюдаемое знач-е критерия принад-лежит критич. обл-ти – г-зу отвергают, если наблюдаемое знач-е критерия принад-лежит обл-ти принятия г-зы – г-зу принимают.Стат. критерием наз. случ. вел-ну К, к-рая служит для проверки нулев. г-зы. Напр, если проверяют г-зу о рав-ве диспер-сий двух норм. ген.совок-тей, то в кач. критерия К принимают отн-ниее исправ-ленных выборочных дисперсий.Выдвинутая г-за может быть правильной или неправильной, поэтому возникает необх-мость ее проверки. В итоге стат. проверки г-зы в двух случаях может быть принято неправильное реш-е, т.е. могут быть допу-щены ошибки двух родов. Ошибка 1-го рода состоит в том, что будет отвергнута правильная г-за. Ошибка 2-го рода – будет принята неправильная.В-ть совершить ошибку перв. рода принято обозначать ч-з λ; ее наз. ур-нем значимости. Наиб. часто ур-нь значимости принимают равным 0.05 или 0.01. Если напр принят ур-нь значи-мости 0.05, то это означает, что в пяти случаях из100имеется риск допустить ошиб-ку перв. рода.Мощ-тью критерия наз. в-ть попадания критерия в критич. обл-ть при условии, что справедлива конкурирующая г-за. Др. словами, мощ-ть критерия есть в-ть того, что нулевая г-за будет отвергнута, если верна конкурирующая г-за. Если ур-нь значимости уже выбран, то критич. обл-ть следует строить так, чтобы мощ-ть критерия была максимальной. Выполнение этого требования должно обеспечить минимальную ошибку второго рода, что, конечно, желат-но.
============================================================
№26(1)Центральная предельная теорема, следствия (теоремы Муавра-Лапласа).
Известно, что нормально распределенные случ. вел-ны широко распространены на практике. Чем это объясняется? Ответ на этот вопрос был дан выдающимся русским математиком А. М. Ляпуновым (центральная предельная теорема): если случ. вел-на Х представляет собой сумму оч. большого числа взаимно независ. случ. вел-н, влияние' каждой из к-рых на всю сумму ничтожно мало, то Х имеет рас-пред-е, близкое к нормальному. Пример. Пусть производится измерение нек-рой физической вел-ны. Любое измерение дает лишь приближенное знач-е измеряемой вел-ны, так как на результат измерения влияют оч. многие независимые случ. факторы (температура, колебания прибора, влажность, и др.).-Каждый из этих факторов порождает ничтожную «частную ошибку». Однако, поскольку число этих факторов оч. велико, их совокупное действие порождает уже заметную «суммарную ошибку».Рассматривая суммарную ошибку как сумму оч. большого числа взаимно независ. частных ошибок, мы вправе заключить, что суммарная ошибка имеет распред-й, близкое к нормальному. Опыт подтверждает справедливость такого заключения.Приведем формулировку центральной Предельной теоремы, к-рая устанавливает условия, при к-рых сумма большого числа слагаемых имее распред-е, близкое к нормальному. Пусть Х1, Х2, …. Хn – по=>сть независ. случ. вел-н, каждая из к-рых имеет конечные матем. Ожидание и дисперсию:
Введем обознач-е:
Обозначим ф-цию распред-я нормированной суммы ч-з:
Говорят, что к по=>сти Х1, Х2…. Применима цент. Предельная теорема, если при любом х ф-я распред-я нормированной суммы при _______ стремится к норм. ф-ции распред-я:
В частности, если все случ. Вел-ны Х1, Х2 … одинаково распределены, то к этой по=>сти применима центр. Предел. Теорема, если дисперсии всех вел-н ________________ конечны и отличны от нуля. Ляпунов доказал, что если для _______ при _________ отн-ниее Ляпунова
Стремиться к нулю (условие Ляпунова), то к по=>сти Х1, Х2 …. Применима ц.п.т. Сущность условия Ляпунова состоит в требовании, чтобы каждое слагаемое суммы ____________ оказывало на сумму начтожное влияние.
Теоремы Муавра-Лапласа.
Локальная теорема Лапласа и дает асимтотическую ф-лу, к-рая позволяет приближенно найти в-ть появл-я соб-я ровно k раз в n исп-ях, если число исп-й достаточно велико. Для частного случая р=1/2, асимтотическая ф-ла была найдена в 1730г. Муавром, в 1783 Лаплас обобщил ее для произвольного р, отличного от 0 и 1. Д-во этой ф-лы довольно сложно, поэтому мы его не приводим. Локальная теорема Лапласа. В-ть того, что в n независ. исп-ях в кажд. из к-рых в-ть появл-я соб-я А равно р причем 1>р>0, то это соб-е наступает ровно m раз приблизительно равна знач-ю ф-ции:
Имеются таблицы в к-рых помещены знач-я ф-ции ___________________________, соответствующие положительным знач-ям аргумента х. Для отриц. Знач-й аргумента пользуются теми же таблицами, как как ф-я ______ четна, т.е. _____________. Итак в-ть того, что соб-е А появится в n независ. исп-ях ровно k раз, приближенно равна:

Интегральная теорема Лапласа. Предположим, что производится n исп-й, в кажд. из к-рых в-ть появл-я соб-я А постоянна и равно р(от 0до 1). Как вычислить в-ть Рn (k1, k2) того, что соб-е А появится в n исп-ях не менее k1 и не более k2. На этот вопрос отвечает интегр. Теорема Лапласа (д-ва опускаем). Теорема: раз в-ть того, что в n независ. исп-ях в кажд. из к-рых в-ть появл-я соб-я А равно р, причем 1>р>0, то соб-е А наступит не менее m1 раз и не более m2 раза приблизительно равно

При решении задач, требующих применения инт. Теоремы, пользуются спец. Таблицами, так как неопред. интеграл ___________ не выражается ч-з элемен-тарные ф-ции. В ней даны знач-я ф-ции _______ для положит. Знач-й х и для х=0, для х<0 пользуются той же табл.й (т.к. ф-я ______ нечетка). Ф-цию _______ часто наз. Ф-ей Лапласа. Вер-ть того, что соб-е А появится в n исп-ях от к1 до к2 раз:
=====================================================
(2) Сравнение исправленной выборочной дисперсии с гипотетической генер. дисперсией норм. совок-ти. Пусть генер. совок-ть распределена нормально, при-чем генер. дисперсия хотя и неизвестна, но имеются основания предполагать, что она равна гипотет. (предполагаемому) знач-ю _____ (стр. 293). На практике уста-навливается на основании предшествую-|щег6 опыта иди теоретически. Пусть из генер. совок-ти извлечена выборка объема ___ и по ней найдена исправленная выборочная дисперсия __________________ степенями свободы. Требуется по исправленной дисперсии при заданном ур-не значимости проверить рулевую г-зу, состоящую в том, что генер. дисперсия рассматриваемой совок-ти равна гипотет. знач-ю _____. Учитывая, что S2 явл. несмещенной оценкой генер. дисперсии, нулевую г-зу можно записать так:
Итак, требуется проверить, что матем. ожидание исправленной дисперсии равно гипотет.»иачению генер. дисперсии. Др. словами, требуется, установить, значимо или незначимо различаются исправленная выборочная и гипотетическая генер. дис-персии. На' практике рассм-мая г-за проверяется, если нужно Проверить точ-ть при-боров, инструментов, станков, методов исследования и уст-ть тех. процессов. Напр, если известна допустимая хар-ка рассеяния контролируемого размера деталей, изго-тавливаемых станком-автоматом, равная ______ найденная по выборке окажется значимо больше _______ станок требует подналадки. В кач. критерия проверки ну-лев. г-зы при мем случ. вел-ну ___________. Эта вел-на случ., потому что в разных опытах S2 принимает различные, наперед неизвестные знач-я. Поскольку можно доказать, что она имеет распред-е _______________ степенями свободы, обозначим
ч-з ____.Итак, критерий проверки нулев. г-зы
Критическая обл-ть строится в зависимости от вида конкурирующей г-зы. Первый случай. Нулевая г-за _______________ Конкурирующая г-за __________________
В этом случае строят правостороннюю критич. обл-ть, исходя из требования, чтобы в-ть попадания критерия в эту обл-ть в предположении справедливости нулев. г-зы была равна принятому ур-ню значимости:
Критич. точку ___________ находят по табл. критич. точек распред-я ______, тогда правосторонняя критическая обл-ть определяется нерав-вом _________, а обл-ть принятия нулев. г-зы - нерав-вом _______________. Обозначим знач-е критерия, вычисленное по данным наблюдений, ч-з __________ и сформулируем правило проверки нулев. г-зы. Правило 1. Для того чтобы при заданном ур-не значимости проверить нулевую г-зу _____________ о рав-ве неизвестной генер. дисперсии норм. совок-ти гипотет. знач-ю при конкурирующей г-зе _______________ надо вычислить наблюдаемое знач-е критерия ________________ и по табл. критич. точек распред-я заданному ур-ню значимости __ и числу степеней свободы __________критич. точку ________.
Если ____________ - нет оснований отвергнуть нулевую г-зу. Если ____________ - нулевую г-зу отвергают. Второй случай. Нулевая г-за ______________.Конкурирующая г-за ___________________.
В этом Случае строят двустороннюю критич. обл-ть, исходя из требования, чтобы в-ть попадания критерия в эту обл-ть в предположении справедливости нулев. г-зы была равна принятому ур-ню
значимости ____. Критич. точки—левую и правую границы критич. обл-ти—находят, требуя, чтобы в-ть попадания критерия в каждой из двух интервалов критич. обл-ти была равна __/2:
В табл. критич. точек распред-я ____ указаны лишь «правые» критич. точки, поэтому возникает кажущееся затруднение в отыскании «левой» критич. точки. Это затруднение легко преодолеть, если принять во внимание, что соб-я ___________________________ противоположны и, =>, сумма их в-тей равна ед-це:
Отсюда
Мы видим, что левую критич. точку можно искать как правую (и значит, ее можно найти по табл.), исходя из требования, чтобы вер-ть попадания критерия в интервал, расположенный правее этой точки, была равна ____________. Правило 2 для того чтобы при заданном ур-не значимости ____ проверить нулевую г-зу о рав-ве неизвестной генер. дисперсии ____ норм. совок-ти гипотет. знач-ю ______ при конкурирующей г-зе _______________, надо вычислить наблюдаемое знач-е критерия ________________ и по табл. найти левую критич. точку __________________ и правую критич. Точку ______________. Если ________________________ - нет оснований отвергнуть нулевую г-зу. Если ________________ или ____________________ - нулевую г-зу отвергают. Третий случай: конкурирующая г-за ______________. Правило 3: при конкурирующей г-зе _______________ находят критич. точку _____________. Если ________________________ - нет оснований отвергнуть нулевую г-зу. Если ________________ или ____________________ - нулевую г-зу отвергают.
===================================================





 = 1/n *
= 1/n *  = 1/n * n * mx = mx
= 1/n * n * mx = mx
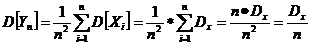

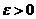
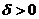 близко к 0
близко к 0 , где
, где  и
и 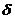 сколь угодно положительные числа
сколь угодно положительные числа 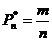 - (в-ть). m-произошло соб-е. n-число опытов.
- (в-ть). m-произошло соб-е. n-число опытов.




