Билет 4.
Пространство элементарных соб-й. Операции над соб-ями.
Мн-во всех элем. соб-й, к-рые могут появиться в исп-и, наз. простр-вом элем. соб-й, а сами элем. соб-я - точками эт. простр-ва. Оп-ции слож-я и умн-я в соб-и обладают след. св-вами:
1.А+В=В+А - коммутативность слож-я
2.А+(В+С)=(А+В)+С - ассоциативность слож-я
3.АВ=ВА - коммутативность умнож-я
4.А(ВС)=(АВ)С - ассоциативность умнож-я
5.А(В+С)=АВ+АС -; А+ВС=(А+В)(А+С) - законы дистрибутивности
см.1лекцию - квадратики
Билет№7
(1) Условн. вер-ть. Теорема умн-я в-тей. Произв- ем двух соб-й А и В наз. соб-е АВ, состоящее в совместном появл-и этих соб-й (А-деталь годная, В-деталь окрашенная, АВ- годная и окрашенная). Произ-ем неск.соб-й наз. соб-е сост-ее в совместном появл-и всех этих соб-й. Во введении случ. соб-е определено как соб-е, к-рое при осущ-нии совок-ти усл- й S может произойти или не произойти. Если при вычислении в-ти соб-я никаких др. ограничений, кроме усл-й S, не нала-гается, то такую в-ть наз. безусловной; если же налагаются и др. доп. усл-я, то в-ть соб-я наз. условной. Напр, часто вычисляют в-ть соб-я В при доп. усл-и, что произошло соб-е А. Заметим, что и безусл. в-ть, строго говоря, явл. условной, поскольку предполагается осущ-ние усл-й S. Усл. вер-тью Ра(В) наз. в-ть соб-я В, вычисленную в Предположении, что соб-е А наступило: Ра(в)=Р(АВ)/Р(А) (Р(А)>0). Рассм-м два соб-я А и В, пусть в-ти Р(А) и Ра(В) известны. Как найти совмещение этих соб-й,т.е. в-ть того что появится и соб-е А и соб-е В. Ответ на этот вопр. дает теорема умн-я: вер-ть совместн. появл-я двух соб-й равна произв-ю в-ти одного из них на усл. вер-ть другого, вычис-ленную в предположении, что перв. соб-е уже наступило Р(АВ)= Р(А)*Ра(В). Д-во: по опред-ю усл. вер-ти Ра(В)=Р(АВ)/Р(А), отсюда Р(АВ)=Р(А)*Ра(В). Следствие: вер-ть совместн. появл-я неск. соб-й равна произв-ю в-ти одного из них на усл. в-ти всех остальных, причем вер-ть каждого послед. соб-я вычисляется в предположении, что все предыдущие соб-я уже появились
Где______________________ вер-ть соб-я ______. Вычисленная в предположении, что соб-я ___________________ наступили. В частности, для трех соб-й___________________________________ (порядок может быть выбран любой, безразлично какое соб-е считать перв., вторым).
======================================================
Билет№9
(1) Ф-ла Бейеса
Пусть соб-е А мож. наступить при усл. появл-я одного из несовм. соб-й В1, В2,… Вn, обр-щих полн. группу. Поскольку заранее не известно, какое из этих соб-й наступит, их наз-т г-зами. Вер-ть появл-я соб-я А опред-ся по ф-ле полн. вер-ти:
Допустим, что произведено испыт-е, в рез. к-рого появилось соб-е А. Поставим своей задачей опред-ть, как изменились (в связи с тем, что соб-е А уже наступило) вер-ти гипотез. Др. словами, будем искать усл. вер-ти.
Найдем сначала усл. вер-ть Ра(В1). По теореме умнож-я имеем
Отсюда
Заменив здесь Р(А) по ф-ле (*), получим
Аналогично выводятся ф-лы, опред-щие усл. вер-ти остальных гипотез, т.е. усл. вер-ть любой г-зы ______________ м.б. вычис-лена по ф-ле
Полученные ф-лы наз. ф-лами Бейеса (по имени англ. Математика, к-рый их вывел в 1764г). Эти фор-лы позвол. переоценить в-ти гипотез после того, как становится известным рез-т испыт-я, в итоге к-рого появилось соб-е А.
======================================================
Билет 6.
1. Теорема слож-я в-тей.
Суммой А+В двух соб-й А и В наз. соб-е, сост-ее в появлении соб-я А, или соб-я В, или обоих этих соб-й. Суммой неск. соб-й наз. соб-е, к-рое сост. в появл-и хотя бы одного из этих соб-й.
Теорема. В-ть появл-я одного из двух несовм. соб-й, безразл. какого, равна сумме в-тей этих соб-й: Р(А+В)=Р(А)+Р(В)
Док-во:n-общ. число возм. элем. исходов испыт-я, m1 –число исходов, благопр. соб-ю А, m2- число исходов, благопр. соб-ю В. Число элем. исходов, благопр. наступл-ю либо соб-я А, либо соб-я В, равно m1+m2. =>, Р(А+В)= (m1+m2)/n=m1/n+m2/n. Приняв во внимание, что m1/n=Р(А) и m2/n = Р(В), окончательно получим Р(А+В)= Р(А)+Р(В).
Следствие. В-ть появл-я одного из неск. попарно несовместных соб-й, безразл.какого, равна сумме в-тей этих соб-й: Р(А1 + А2+ …+Ап)=Р(А1) +Р(А2)+ …Р(Ап).
Д-во: Рассм-м 3 соб-я: А, В, С. Т.к. рассм-мые соб-я попарно несов-местны, то появл-е одного из трех соб-й, А, В и С, равносильно на-ступл-ю одного из двух соб-й, А+В и С, поэтому в силу указ-ой теоре-мы Р(А+В+С)=Р((А+В)+С)=Р(А+В)+Р(С)=Р(А)+Р(В)+Р(С)
Полная группа соб-й.
Теорема: Сумма в-тей соб-й А1, А2,…,Ап, обр-щих полн.группу равна 1.
Д-во: так как появл-е одного из соб-й полной группы достоверно, в-ть достоверного соб-я равна 1, то Р(А1+А2+ …+Ап)=1 (1)
Любые два соб-я полн. группы несовместны, поэтому можно применить теорему слож-я: Р(А1+А2+…+Ап) =Р(А1) +Р(А2)+ …+Р(Ап) (2)
Сравнивая (1) и (2), получим Р(А1) +Р(А2)+ …+ Р(Ап)=1
Противоположные соб-я.
Против-ными наз. два единственно возм. соб-я, обр-щих полн. группу.
Теорема: сумма в-тей противоп. соб-й равна 1: Р(А)+Р(А)=1
Д-во: Противоп. соб-я обр-ют полн. группу, а сумма в-тей соб-й, обр-щих полн. группу равна 1.
2.Система дифференциальных ур-ний Колмогорова для в-тей соб-й. Переходы системы из Si в Sg происходит под воздействием простейшего потока с интенсивностью λig. Граф состояния системы с проставленными у стрелок интенсивностями будем называть размеченным
Очевидно, что для любого момента t: Σ3i=10 Pi(t)=1
Рассм-м с-му в момент t и задав малый промежуток ∆t, найдем в-ть: P0(t+∆t) того, что с-ма в момент t+∆t будет находиться в сост-и S0. Это достигается разн. способами:1.с-ма в момент t находилась в сост-и S0, а за время ∆t не вышло из него. Вывести с-му можно суммарным прос-тейш. потоком с интенсив-ю (λ01 + λ02), т.е. с в-тью (λ01 + λ02)∆t. 2.с-ма в момент t с в-тями P1 или P2 находятся в сост-и S1 и S2 и за время ∆t перешла в S0. Потоком λ10 с-ма перех-т в сост-е S0. Применяя подобные изм-я, получим P0(t+∆t)=P1(t) λ10 ∆t +P2(t) λ20∆t +P0(t) [1-(λ01 + λ02)∆t]
При переходе можно получить:
1.P’0= λ10P1 + λ20P2 – (λ01 - λ02)P0
2.P’1= λ01 P0 + λ31P3 – (λ01+λ13)P1
3.P’2=λ02P0 + λ32P3 – (λ20 + λ23)P2
4.P’3 = λ13P0 + λ23P2 – (λ20 +λ23)P3
===================================================
Билет 8.
(1) Ф-ла полн. в.ти
Пусть люб. соб-е А мож. наступить при усл.появл-я одного из несовм. соб-й В1, В2, В3, Вn, к-рые обр-ют полн. группу. Пусть известны в-ти этих соб-й и усл. в-ти ______________________ соб-я А. Как найти в-ть соб-я А? Ответ дает теорема пол. вер-ти: вер-ть соб-я А, к-рое может наступить лишь при усл. появл-я одного из несовм.соб-й В1, В2.. Вn, обр-щих полн. группу, равна сумме произв-й в-тей кажд. из этих соб-й на соотв-щую усл. в-ть соб-я А:
Д-во: по усл., соб-е А мож. наступить, если наступит одно из несовм. соб-й В1, В2… Вn. Др. словами, появл-е соб-я А означает осущ-ние одного, безразл. какого, из несовм. соб-й В1А, В2А,…. ВnА. Пользуясь для вычисления вер-ти соб-я А теоремой слож-я получим:
Остается вычислить каждое из слагаемых. По теореме умнож-я вер-тей зависимых соб-й имеем:
Подставив правые части этих равенств в соотн-ниее (*), получим ф-лу полной вер-ти
2.Предмет мат.статистики. Генер. совок-ть и выборка.
Перв. задача мат.статистики – указать способы сбора и группировки стат. сведений, полученных в рез. наблюдений или в рез.спец-но по-ставленных экспериментов. Втор. задача – разработать методы анализа стат. данных в завис-ти от целей исслед-я.
Совр. мат.стат. разрабатывает способы опред-я числа необх. испыт-й до начала исследования (планирование эксперимента), в ходе исслед-я (последовательный анализ) и решает многие др. задачи. ЕЕ опред-ют как науку о принятии решений в усл. неопред.сти.
Выборка – это совок-ть случ-но отобранных объектов. Генеральн. со-вок-ть – это совок-ть объектов, из к-рых производится выборка.
Выборка: повторная – при к-рой отобранный объект (перед отбором следующего) возвращается в генерал. сов-ть; бесповторная – про к-рой отобранный объект в генер. сов-ть не возвращается (исп-ется на прак-тике). Выборка должна правильно представлять пропорции генер. сов-ти, т.е. она должна быть репрезентативной (будет такой, если ее осущ-ть случайно: кажд. объект выборки отобран случ-но из генер. сов-ти, если все объекты имеют одинак. в-ть попасть в выборку).
======================================================
Билет 30. 1Предмет мат.статистики. Генер. совок-ть и выборка.
Первая задача мат.статистики – указать способы сбора и группировки стат. сведений, полученных в рез-те наблюдений или в рез-те специально поставленных экспериментов. Вторая задача – разработать методы анализа стат. данных в зависимости от целей исследования.
Современная мат.статистика разрабатывает способы опред-я числа необходимых исп-й до начала исследования (планирование эксперимента), в ходе исследования (последовательный анализ) и решает многие др. задачи. ЕЕ определяют как науку о принятии решений в условиях неопред.сти.
Выборка – это совок-ть случайно отобранных объектов. Генер. совок-ть – это совок-ть объектов, из к-рых производится выборка.
Выборка: повторная – при к-рой отобранный объект (перед отбором следующего) возвращается в генеральную совок-ть; бесповторная – про к-рой отобранный объект в генеральную совок-ть не возвращается (исп-ется на практике). Выборка должна правильно представлять пропорции генер. совок-ти, т.е. она должна быть репрезентативной (будет такой, если ее осуществить случайно: каждый объект выборки отобран случайно из генер. совок-ти, если все объекты имеют одинаковую в-ть попасть в выборку).
==============================================================
Билет№10
(1)Опеределение случ. Вел-ны. Ряд распред-я.
Уже в первой части приводились соб-я, состоящие в появлении того или иного числа. Напр,. при бросании игральной кости могли появиться числа 1, 2, 3, 4, 5 и 6. Наперед опред-ть число выпавших очков невозможно, поскольку оно зависит от многих случ. причин, к-рые полностью не могут быть учтены. В этом смысле число очков есть вел-на случ.; числа 1, 2, 3, 4, 5 и 6 есть возм. знач-я этой вел-ны. Случ. наз. вел-ну, к-рая в рез-те исп-я примет одно и только одно возможное значе-/ ние, наперёд не известное и зависящее от случ." причин, к-рые заранее не могут быть учтены. Будем далее обозначать случ. вел-ны прописными буквами X, Y, Z, а их возм. знач-я—соответствующими строчными буквами х, у, 'г. Напр если случ. вел-на Х имеет три возм. знач-я, то они будут обозначены так: х1, х2, х3.
Вернемся к примерам, приведенным выше. В первом из них случ. вел-на Х могла принять одно из следующих возм. знач-й: 0, 1, 2,..., 100. Эти знач-я отделены одно от другого промежутками, в к-рых нет возм. знач-й X. Таким образом, в этом примере случ. вел-на принимает отдельные, изолированные возм. знач-я. Во втором примере случ. вел-на могла принять любое из знач-й промежутка (а, Ь). Здесь нельзя отделить одно возможное знач-е от другого промежутком, не содержащим возм. знач-й случ. вел-ны.Уже из сказанного можно заключить о целесообразности различать случ. вел-ны, принимающие лишь отдельные, изолированные знач-я, и случ. вел-ны, возм. знач-я к-рых сплошь заполняют нек-рый промежуток. Дискр. (прерывной) наз. случ. вел-ну, к-рая принимает отдельные, изолированные возм. знач-я с определенными вероятностями. Число возм. знач-й дискр. случ. вел-ны может быть конечным или бесконечным. Непрер. наз. случ. вел-ну, к-рая может принимать все знач-я из некот. конечного или бесконечного промежутка. Очевидно, число возм. знач-й непрер. случ. вел-ны бесконечно.На первый взгляд может показаться, что для задания дискр. случ. вел-ны достаточно перечислить все ее возм. знач-я. В действительности это не так: случ. вел-ны могут иметь одинаковые перечни возм. знач-й, а в-ти их — различные. Поэтому для задания дискр. случ. вел-ны недостаточно перечислить все возм. ее знач-я, нужно еще указать их в-ти. Законом распред-я дискр. случ. вел-ны наз. соответствие между возм. знач-ями и их вероятностями; его можно задать таблично, аналитически (в виде ф-лы) и графически. При табличном задании закона распред-я дискр. случ. вел-ны первая строка таблицы содержит возм. знач-я, а вторая—их в-ти:
Приняв во внимание, что в одном исп-и случ. вел-на принимает- одно и только одно возможное знач-е, заключаем, что соб-я _____________________________образуют полную группу; =>, сумма в-тей этих соб-й, т. е. сумма в-тей второй строки таблицы, равна ед-це:
Если множество возм. знач-й Х бесконечно (счетно), то ряд ________________сходится и его сумма равна ед-це. Для наглядности закон распред-я дискр. случ. вел-ны можно изобразить и графически, для чего в прямоугольной системе координат строят точки _______,а затем соединяют их отрезками прямых. Полученную фигуру наз. многоугольником распред-я.
=====================================================
(2) Метод наиб. правд-бия Одним из методом точечн. оценки неизвестн. парам-ров распред-я явл. Метод наиб. правд-бия, предложенный Фишером. А) Дискр. случ. Вел-ны. Пусть Х дискр. Случ. Вел-на, к-рая в рез-те n испыт-й приняла знач-я х1, х2, хn. Допустим, что вид закона распред-я вел-ны Х задан, но неизвестен парам-р _____, к-рым опред-ся этот закон. Требуется найти его точечн. оценку. Обозначим вер-ть того, что в рез-те испыт-я вел-на Х примет знач-е хi (i=1,2,n), ч-з р(_________)(стр. 229). Ф-цией правд-бия диск. Случ. Вел-ны Х наз. ф-цию аргумента _____
Где х1, х2, хn – фиксир. числа. В кач. точечн. оценки парам-ра ____ приним. такое его знач-е ______________________, при к-ром ф-ция правдоп-я достигает максимума. Оценку ____ наз. оценкой наиб. прав-доподобия. Ф-ции L и InL достигают макс-ма при одном и том же знач-и ____, поэтому вместо отыскания макс-ма ф-ции L ищут (что удобнее) мах ф-ции InL. Логарифмич. ф-ей правдоп-я наз. ф-ю InL. Как известно, точку мах ф-ции InL аргумента ____ можно искать, напр. так: 1) найти производную ______
2) приравнять произв-ю нулю и найти критич. точки – корень полу-ченного ур-я (его наз. ур-ем правд-бия). 3) найти вторую произ-ю
если вторая произв-я при __________ отриц-на, то ____ - точка мах. Найденную точку мах ____приним. в кач. оценки наиб. правд-бия парам-ра ___. Метод наиб. правд-бия имеет ряд достоинств: оцен-ки наиб. правд-бия состоятельны (но они м.б. смещенными), распределены асимптотически нормально (при больших знач-ях л прибли-женно нормальны) и имеют наим. дисперсию по сравн. с др. асимпто-тически нормал. оценками; если для оцениваемого пар-ра 6 сущ-ет эффективн. оценка О*, то ур-е правд-бия имеет единств. реш-е 6*; этот метод наиб. полно исп-ет данные выборки об оцениваемом парам-ре, поэтому он особ-но полезен в случ. малых выборок.
Недостаток метода состоит в том, что он часто требует сложн. вычис-лений. Б) Непрерыв. случ. Вел-ны. Пусть Х непрер. случ. Вел-на, к-рая в рез-те n исп-й приняла знач-я х1, х2, хn. Допустим, что вид плот-ти распред-я f(x) задан, но не известен пар-р _____, к-рым опред-ся эта ф-я. Ф-цией правд-бия непрерыв. Случ. Вел-ны Х наз. ф-ю аргумента:
Где х1, х2, хn – фиксир. числа. Оценку наиб. правд-бия неизвест. пар-ра распред-я непрер. случ. Вел-ны ищут так же как и в случ. дискр.вел-ны.
======================================================
(2) Доверитель. интервал для МО при известной дисперсии. (при известн. СКО стр. 214) Пусть количеств. признак Х генеральн. совок-ти распределен нормально, причем СКО ___ этого распред-я известно. Требуется оценить неизвестное МО __ по выборочной ср. ___. По-ставим своей задачей найти доверительные интервалы, покрывающие парам-р ___ с надеж-ть ____. Будем рассм-ть выборочную ср. ____ как случ. вел-ну ____ (___ изменяется от выборки к выборке) и выборочн. знач-я признака х1, х2, хn – как одинаково распред-ные независ. случ. вел-ны Х1, Х2, Хn (эти числа также изм-ся от выборки к выборке). Др. словами, МО каждой из этих вел-н равно ___ и СКО - ____. Примем без док-ва, что если случ. вел-на Х распределена норм-но, то выбо-рочная ср. ____, найденная по независ. наблюдениям, также распр-на норм-но. Парам-ры распред-я ____ таковы:
Потребуем, чтобы выполнялось соотн-ниее:
Где____ заданная надеж-ть. Пользуясь ф-лой
Заменив Х на _______ и ______ на __________________, получим
Где _____________. Найдя из последнего рав-ва ________________, можем написать
Приняв во внимание, что вер-ть Р задана и равна ____, окончательно имеем (чтобы получить рабочую ф-лу, выборочную ср. вновь обозначим ч-з ______)
Смысл полученного соотн-ниея таков: с надеж-тью _____ можно утверждать, что довер. Интервал ___________________________ покрывает неизвестный парам-р ____ точ-ть оценки ____________________. Число t определяется из рав-ва _______________ или _______________; по табл. ф-ции Лапласа находят аргумент t, к-рому соответствует знач-е ф-и Лапласа равное ________.
==================================================
2.Точеч. оценка числ. хар-к. Осн. опред-я. Метод моментов. Точечн. наз. оценку, к-рая опред-ся одним числом. Оценка генер. дисперсии по исправленной выборочной. Пусть из генер. сов-ти в рез. n независ. наблюдений над колич-ным признаком X извлечена повторн. выборка объема n:
знач-я признака х1х2 хк
частоты n1n2 nк
При этом n1+n2+ +nk=n
Требуется по данным выборки оценить неизвестную генер. дисперсию Dr. Если в кач. оценки генер. дисперсии принять выборочн. дисперсию, то эта оценка будет приводить к систематич. ошибкам, давая занижен. знач-е генер. дисперсии. Объясняется это тем, что, как можно доказать, выборочная дисперсия явл. смещенной оценкой Dr, др. словами, мат.ожидание выборочной дисперсии не равно оцениваемой генер. дисперсии, а равно
M[Dв]=((n-1)/n)Dr
Получим исправл-ю дисперсию, к-рую обычно обозн-ют ч-з s2
см.стр.212
Исправл-я дисп-я явл, конечно, несмещенной оценкой генер. дисп-и. Действ-но
Итак, в кач. оценки генер. дисп-ии принимают исправл. дисперсию
Для оценки же ср. квадр. отклонения генер. сов-ти исп-ют “исправленное” СкО, к-рое равно квадр. корню из исправл. дисперсии:
Подчеркнем, что s не явл. несмещен. оценкой; чтобы отразить эт. факт, мы будем писать так: “исправленное” ско.
Метод моментов.
ММ, предложенный Пирсоном осн. на том, что начальн. и центральн. эмперич. моменты явл.состоятельными оценками соотв-но начальн. и центр. теор. мом-тов того же порядка. Достоинство метода – сравнит-ая его простота. ММ точечн. оценки неизвестн.парам-ров заданного распред-я сост. в приравнивании теор. моментов рассм-го распред-я соотв-щим эмпир.моментам того же порядка. А.Оценка одного парам-ра: для оценки одного парам-ра достаточно иметь олно ур-е отн-ьно этого парам-ра. Следуя методу м., приравняем, напр, начальн. теор. момент перв. порядка к нач. эмпир. моменту перв. порядка:
стр.227
(1)
МО М(Х), как видно из соотн-ниея
есть ф-я от,поэтому (1) можно рассм-ть как ур-ие с одним неизв . Решив это ур-е отн-но праметра , тем самым найдем его точечную оценку 1, к-рая явл. ф-цией от выборочн. ср., => и от вариант выборки:
Билет№13
(1) Дисперсия случ. вел-ны и ее св-ва
На практике часто требуется оценить рассеяние возм. знач-й случ. вел-ны вокруг ее ср. знач-я. Напр, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, к-рая должна быть поражена.На перв. взгляд может показаться, что для оценки рассеяния проще всего вычислить все возм. знач-я отклонения случ. вел-ны и затем найти их ср. знач. Однако такой путь ничего не даст, так как ср. знач. отклонения, т. е. М[Х—М(Х)], для люб. случ. вел-ны равно нулю. Это св-во уже было доказано в предыд. параграфе и объясн. тем, что одни возм. отклонения положительны, а др.—отрицательны; в рез. их вза-имн.погашения ср. знач. отклонения равро нулю. Эти соображения говорят о целесообр-ти заменить возм. отклонения их абс. знач-ми или их квадратами. Так и поступают на деле. Правда, в случае, когда возм. отклонения заменяют их абс. знач-ми, приходится оперир-ть с абс.вел-нами, что приводит иногда к серьезн. затруднениям. Поэтому чаще все-го идут по др.пути, т. е. вычисляют ср. знач. квадрата откл-ия, к-рое и наз. дисперсией. Дисперсией (рассеянием) диск. случ. вел-ны наз.МО квадрата отклонения случ. вел-ны от ее МО:
Пусть сл. вел-на задана законом распред-я:
Тогда квадрат отклонения имеет след. закон распре-я:
По определению дисперсии,
Т.о., чтобы найти дисп-ю, достат-но вычислить сумму произ-й возм. знач-й квадрата отклонения на их вер-ти. Теорема: дисперсия равна разности между МО квадрата случ. Вел-ны Х и квадратом ее МО:
Св-во№1: дисп. постоянной вел-ны С равна нулю. Д-во: по опред-ю дисп-ии
Пользуясь перв. св-вом МО (МО постоянной равно самой посто-янной), получим
Итак:
Св-во№2: постоян. множ-ль можно выносить за знак дисп-ии, возводя его в квадрат:
Д-во: по определению дисперсии имеем
Пользуясь вторым св-вом МО(постоян. множ-ль можно выносить за знак МО), получим
Итак,
Св-во№3: дисперсия суммы двух независ. случ. Вел-н равна сумме дисп-й этих вел-н:
Д-во: по ф-ле для вычисления дисперсии имеем:
Раскрыв скобки и пользуясь св-вами МО суммы неск. вел-н и произ-я двух независ. случ. Вел-н, получим
Итак,
Следствие1: дисп-сия суммы неск. взаимно независ. случ. Вел-ин равна сумме дисп-й этих вел-н. Напр, для 3-х слагаемых:
Следствие2: дис-я суммы постоянной вел-ны и случ. Равна дисперсии случ. Величны:
Д-ва: вел-ны С и Х независимы, поэтому, по третьему св-ву
В силу перв. сво-ва ____________. =>___________________________________ Св-во№4: дисперсия разности двух независ. случ. Вел-н равна сумме их дисперсий:
Д-во: в силу третьего св-ва
По второму св-ву,
Или
===================================================
Билет 11.
Билет№15
(1) Закон распред-я Пуассона; пуассоновское распред-е как преде-льное для биноминального. Пусть производится п независ. исп-й, в кажд. из к-рых в-ть появл-я соб-я А равна р. Для опред-я в-ти k появл-й соб-яв этих исп-ях исп-ют ф-лу Бернулли. Если же п велико, то польз-ся асимптотич. ф-лой Лапласа. Однако эта ф-ла непригодна, если в-ть соб-я мала (p^O.l). В эт. случаях (n велико, р мало) прибегают к асимптотич. ф-ле Пуассона. Итак. поставим перед собой задачу найти в-ть того, что при оч. больш. числе исп-й, в кажд. из к-рых в-ть соб-я оч. мала, соб-е наступит ровно k раз. Сделаем важн. допущение: Произв-е nр сохраняет постоян. знач-й, а именно ________. Как будет следовать из дальнейш.это означает, чти ср. число появлений соб-я в разл. сериях исп-й, т. е. при разл. знач-ях n, остается неизм-м. Воспользуемся ф-лой Бернулли для вычисл-я интересующей нас в-ти:
Так __________то ______ =>,
Приняв во внимание, что n имеет оч. большое знач-е, вместо _________ найдем ___________При этом будет найдено лишь приближ. знач-е отыскиваемой вер-ти: n хотя и велико, но конечно, а при отыскании
предела мы устремим п к бесконеч-ти. Заметим, что скольку произведение пр сохраняет постоян. знач-е, то при ________ вер-ть _________. Итак
|
К Т.о. (для простоты записи знак приближения рав-ва опущен),
Эта ф-ла выраж. закон распр-я Пуассона вер-тей массов.(n –велико) и редких (р мало) соб-й
Когда требуется спрогнозировать ожидаемую очередь и разумно сбалансир-ть число и производит-ть точек обслуж-я и время ожидания в очереди. Пуассоновским наз. закон распред-я дискр. случ. вел-ны Х числа появл-я некот. соб-я в n-независ. опытах если в-ть того, что соб-е появится ровно m раз определяется по ф-ле.
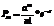 a=np
a=np
n-число проведенных опытов
р-в-ть появл-я соб-я в кажд. опыте
В теории массов.обслуж-я парам-р пуас-кого распред-я опред-ся по ф-ле
а=λt, где λ – интенсив-ть потока сообщений t-время
Необх-мо отметить, что пуас-кое распред-е явл. предел. случаем бином-го, когда исп-й стремится к бесконеч-ти, а в-ть появл-я соб-я в кажд. опыте стремится к 0.
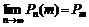
Пуас. распр-е явл. единичн. распр-ем для к-рого такие хар-ки как МО и дисперсия совпадают и они равны парам-ру этого закона распред-я а.
=====================================================
Билет 14.
(1)Схема опытов Бернулли. Бином. зак. распред-я. Ф-ла Бер-нулли Если произв-ся неск. испыт-й, причем в-ть соб-я А в кажд. исп-и не зависит от исходов др. исп-й, то такие исп-я наз. независ-ми отн-но соб-я А.В разн. незав. исп-ях соб-е А мож. иметь либо различн. в-ти, либо одну и ту же в-ть. Будем далее рассм-ть лишь такие независ. исп-я, в к-рых соб-е А имеет одну и ту же в-ть.Ниже воспользуемся поня-тием сложн. соб-я, понимая под ним совмещение неск. отдельн. соб-й, к-рые наз. простым.Пусть производится n независ. исп-й, в кажд. из к-рых соб-е А мож.появиться либо не появиться. Условимся считать, что в-ти соб-я А в кажд. исп-ии одна и та же, а именно равна р. =>, в-ть ненаступл-ия соб-я А в кажд. исп-и также постоянна и равна q=1-р. Поставим перед собой задачу вычислить в-ть того, что при п исп-ях соб-е А осуществится ровно k раз и, =>, не осущ-ся n-k раз. Важно подчеркнуть, что не требуется, чтобы соб-е А повторилось ровно k раз в опред.й по=>сти. Напр, если речь идёт о появл-и соб-я А три раза в 4 исп-ях, 'тo возм-ны след. сложн. соб-я: АААА, АААА, АААА, АААА. Запись АААА означ., что в перв., втор. и третьем исп-ях соб-е А наступило, а в четверт. исп-и оно не появилось, т. е. наступило про-тивоп. соб-е А; соответственный смысл имеют и др. записи.Искомую в-ть обозначим,_________ Напр, символ Р5(3) означает в-ть того, что в пяти исп-ях соб-е появятся ровно 3 раза и, =>, не наступит 2 раза. Поставленную задачу можно решить с пом. так наз. ф-лы Бернулли. Вывод ф-лы Бернуллн. В-ть одного сложн. соб-я, сост-го в том, что в п исп-ях соб-е А наступит k раз и не наступит n— k раз, по теореме умнож-я в-тей независ. соб-й равна __________Таких сложн. соб-й м.б. столько, ск. можно составить сочетаний из п эл-тов по k эл-тов, т.е. ____. Так как эти сложн. соб-я несовместны, то по теореме слож-я в-тей несовм. соб-й иском. в-ть равна сумме в-тей всех возм. сложн. соб-й. Поскольку же в-ти всех этих сложн. соб-й одинаковы, то иском. в-ть (появл-я k раз соб-я А в п исп-ях) равна в-ти одного сложн. соб-я, умноженной на их число:
или
Полученную ф-лу наз. ф-лой Бернулли Пусть производится га независ. исп-й, в кажд. из к-рых соб-е А может появиться либо не появиться. В-ть наступления соб-я во всех
исп-ях постоянна и равна р (=>, в-ть непоявл-я q ==1— р). Рассм-м в кач. дискр. случ. вел-ны X число появлений соб-я А в этих исп-ях. Поставим перед собой задачу: найти закон распред-я вел-ны X. Для ее реш-я требуется опред-ть возм. знач-я Х и их в-ти. Очевидно, соб-е А в n исп-ях мож. либо не появиться, либо появиться 1 раз, либо 2 раза,..., либо п раз. Т.о., возм. знач-я Х таковы: ________________________________________Остается найти в-ти этих возм. знач-й, для чего достаточно воспольз-ся ф-лой Бернулли:
(*)
где k =0, 1, 2,..., n
Ф-ла (*) и явл. аналитич. выраж-ем иском. закона распред-я. Биномиальным наз. распред-е в-тей, опред-мое ф-лой Бернулли. Закон назван «бином-ым» потому, что правую часть рав-ва (*) можно рассм-ть как общ. член разложения бинома Ньютона:
Т.о., перв. член разлож-я _____ определяет в-ть наступл-я рассм-го соб-я n раз в n независ. исп-ях; втор. член ____________опред-ет в-ть наступл-я соб-я n—1 раз;...; последн. член q " опред-ет в-ть того, что соб-е не появится ни разу.Напишем бином. закон в виде таблицы:
Бином-ым наз. законы распр-я случ. вел-ны Х числа появл-я не-кот. соб-я в n опытах если в-ть р появл-я соб-я в кажд. опыте постоянна
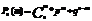
Сумма в-тей представляют собой бином Ньютона

Для опред-я числ. хар-к в биномиальное распред-е подставить в-ть к-рая определяется по ф-ле Бернули.

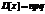
При биномиальном распределении дисперсия равна мат. Ожиданию умноженному на в-ть появл-я соб-я в отдельном опыте.
2.Интервальн. оценка числ. хар-к. Доверительн. интервал. Осн. опред-я. Точечной наз. оценку, к-рая опред-ся одним числом. При выборке малого объема точечн. оценка мож. значит-но отличаться от оцениваемого парам-ра, т.е. приводить к грубым ошибкам. По этой причине при небольш. объеме выборки следует польз-ся интервальн. оценками.
Интервальной наз. оценку, к-рая определяется 2-мя числами - концами интервала. Интервальные оценки позволяют установить точ-ть и надеж-ть оценок. Пусть найденная по данным выборки статистич. хар-ка служит оценкой неизвестн. парам-ра.Будем считать постоян. числом. Если >0 и < , то чем меньше , тем оценка точнее. Т.о., полож. число хар-ет точ-ть оценки.
Однако стат. методы не позвол. категорич-ки утверждать, что оценка удовл. нер-ву ; можно лишь говорить о в-ти , с к-рой это рав-во осущ-ся.
Надеж-тью (доверительной в-тью) оценки по наз. в-ть , с к-рой осущ-ся нерав-во . Обычно надеж-ть оценки задается наперед, причем в кач. берут число, близкое к ед-це.Наиб. часто задают надеж-ть равную 0.95; 0.99; 0.999.Пусть в-ть того, что равна :
см.стр213
Заменив нерав-во равносильным ему двойным нерав-вом или имеем
Это соотне следует понимать так: в-ть того, что интервал заклет в себе неизвестн. парам-р , равна .
Доверительным интервалом наз. интервал , к-рый покрывает неизвестн. парам-р с заданной надеж-тью .
От выборки к выборке будут меняться концы доверительного интервала, т.е. доверит. границы сами являются случайными вел-нами.
=====================================================
Билет 12.
(1) МО дискр. Случ. Вел-ны
МО-ем дискр. случ. Вел-ны наз. сумму произведений всех ее возм. знач-й на их в-ти. Пусть случ. вел-на Х может принимать только знач-я х1, х2, …хn, вер-ти к-рых соотв-но равны р1, р2….рn. Тогда МО М(х) случ. вел-ны Х опред-ся рав-вом:
Если дискр. случ. Вели-наХ приним. счетное мн-во возм. знач-й, то
Причем МО сущ-ет, если ряд в правой части рав-ва сходится абс-но. Итак, МО числа появлений соб-я в одной испыт-и равно вер-ти этого соб-я. Св-во№1: МО постоян. вел-ны равно самой постоянной: М(С)=С. Д-во: будем рассм-ть постоянную С как дискр. случ. вел-ну, к-рая имеет одно возм. знач-е С и принимает его с вер-тью р=1. След-но: М(С)=С*1=С. Св-во№2: постоян. множ-ль можно выносить за знак МО: М(СХ)=СМ(Х). Д-во: пусть случ. Вел-на Х задана законом рас-пред-я вер-тей:
Напишем закон распр-я случ. Вел-ны СХ:
МО случ. Вел-ны СХ:
Итак:
Св-во№3: МО произв-я двух независ. случ. Вел-н равно произв-ю их матем. Ожиданий:________________________. Д-во: пусть независ. случ. Вел-ны Х и У заданы своими законами распред-я вер-тей:
Составим все знач-я, к-рые может принимать случ. Вел-на ХУ. Для этого перемножим все возм. знач-я Х на кажд. возм. знач-е У; в итоге получим ______________. Напишем закон распред-я ХУ, предполагая для простоты, что все возм. знач-я произв-я различны (если это не так, то д-во производится аналогично):
МО равно сумме произведений всех возм. знач-й на их вер-ти:
Или
Итак,
Следствие: МО произв-я неск. взаимно независ. случ. Вел-н равно произв-ю их мат. Ожиданий. Напр, для трех случ. Вел-н имеем:
Св-во№4: МО суммы двух случ. Вел-н равно сумме МО слагаемых:
Д-во: пусть случ. вел-ны Х и У заданы следующими законами расп-я:
Составим все возм. знач-я вел-ны Х+У. Для этого к кажд. возм. знач-ю Х прибавим кажд. возм. знач.е У; получим ____________________________________. Предположим для прос-тоты, что эти возм. знач-я различны, и обозначим их вер-ти соотв-но ч-з __________________ МО вел-ны Х+У равно сумме произв-й возм. знач-й на их вер-ти:
Или
Докажем, что _________________. Соб-е, состоящее в том, что Х примет знач-е х1 (вер-ть этого соб-я равна р1) влечет за собой соб-е, к-рое сост. в том. Что Х+У примет знач-е х1+у1 или х1+у2 (вер-ть этого соб-я по теореме слож-я равна р11+р12), и обратно. Отсюда и следует, что р11+р12=р1. Аналогично док-тся рав-ва
Подставляя правые части этих равенств в соотн-ниее (*) получим
Или окончательно
Следствие: мо суммы неск. случ. Вел-н равно сумме МО слагаемых. Напр для трех слагаемых вел-н имеем:
2.Выборочн. оценивание ф-лой распред-я. Гистограмма.
Для нагляд-ти строят разл. гр-ки стат. распред-я и, в част-ти, поли-гон и гистограмму. Полигон исп-ся для дискр. вел-н. В случае непрер. признака целесообразно строить гистограмму, для чего интервал, в к-ром заключены все наблюдаемые знач-я признака, разбивают на неск. частичн. интервалов длиной h и находят для кажд. частичн. интервала n1 – сумму частот вариантов, попавших в I-тый интервал.
Гистограммой частот наз.ступенчатую фигуру, сост-ю из прямо-угольников, основаниями к-рых служат частичн. интервалы длиною h, а высоты равны отн-ю ni/h (плот-ть частоты). Для построения гисто-граммы частот на оси абсцисс отклад-ют частичн. интервалы, а над ни-ми проводят отрезки, пар-ные оси абсцисс на расст. ni/h. Площадь гис-тограммы частот равна сумме всех частот, т.е. объему выборки.
Гистограммой отн-ных частот наз. ступенчатую фигуру, основаниями к-рой служат частичн. интервалы длиною h, а высоты равны отн-нию Wi/h (плот-ть отн-ной частоты). Для построения этой гист-мы на оси абсцисс отклад-ют частичн. интервалы, а над ними проводят отрезки, пар-ные оси абсцисс на расст. Wi/h. Площадь I-го частичного п/у равна hWi/h = Wi - отн-ной частоте вариант, попавших в I-й интервал. =>, площадь гистограммы отн-ных частот равна сумме всех отн-ных частот, т.е. ед-це.
====================================================
Билет 16.
(1)Геом. закон распред-я дискр. сл. Вел-ны. Пусть произв-ся незав. исп-я, в кажд. из к-рых в-ть появл-я соб-я А равна р (0 < р<1) и, =>, вер-ть его непоявл-я q=1-р. Исп-я заканчиваются, как только появится соб-е А. Т.о., если соб-е А появилось в k-том исп-и, то в предшеств. k-1 исп-ях она не появилось. Обозначим ч-з Х дискрет. Случ. Вел-ну – число исп-й, к-рое нужно провести до перв. появл-я соб-я А. Оче-видно, возм. знач-ями Х явл. Натур. числа: х1=1, х2=2. Пусть в перв. k-1 исп-ях соб-е А не наступило, а в k-том исп-и появилось. Вер-ть



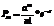 a=np
a=np