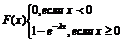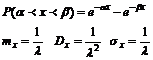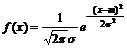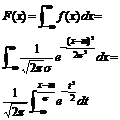Проверка г-зы о значимости коэффициента корреляции.

Пусть двумерная генер. совок-ть (Х,У) распред-на нормально. Из этой совок-ти извлечена выборка объема п и по ней найден выборочный коэффициент кор-реляции r_в, к-рый оказался отличным от нуля. Т.к. выборка отобрана случайно, то еще нельзя заключить, что коэффициент корреляции генер. совок-ти r_г также отли-чен от нуля. Нас интересует именно этот коэффициент, поэтому возникает необх-мость при заданном ур-не значимости                                     проверить нулевую г-зу Н₀:r_г=0 о рав-ве нулю генерального коэффициента корреляции при конкурирующей г-зе Н₁:r_г=0. Если нулевая г-за отвергается, то это означает, что выборочный коэффициент корреляции значимо отличается от нуля, а Х и У коррелираваны, т.е. связаны линейной зависимостью. Если нулевая г-за будет принята, то выборочный коэффициент корреляции незначим, а Х и У некоррелированны, т.е. не связаны линейной зависимостью

В кач. критерия проверки нулев. г-зы примем случ. вел-ну

см. стр328

Вел-на Т при справедливости нулев. г-зы имеет распред-е Стьюдента с k=n-2 степенями свободы.Поскольку конкурирующая г-за имеет вид r_г неравно 0, критическая обл-ть двусторонняя.Обозначим знач-е критерия, вычесленное по данным наблюдений, ч-з Т_набл и сформулируем правило проверки нулев. г-зы.

Правило. Для того чтобы при заданном ур-не значимости проверить нулевую г-зу о рав-ве нулю генерального коэффициента корреляции ннорм. двумерной случ. вел-ны при конкурирующей г-зе, надо вычислить наблюдаемое знач-е критерия:

Tтабл = r_b√n-2/√1-r²_b и по табл. критич. точек распред-я Стьюдента, по заданному ур-ню значимости и по числу степеней свободы k=n-2 найти критич. точку t_кр(альфа, k) для двусторонней критич. обл-ти

Если Т_наблпо модулю < t_кр - нет оснований отвергнуть нулевую г-зу

Если Т_набл по модулю >t_кр - нулевую г-зу отвергают

Билет 21.

(1) Показательный закон распред-я

Показат. Наз. распред-е в-тей непрер. случ. Вел-ны Х, к-рое описывается плот-тью

 

Где_____ постоянная положительная вел-на. Показат. Расп-е определяется одним парам-ром_____. Эта особ-ность показат. Распред-я указывает на его преимущество по сравнению с распред-ями, зависящими от большего числа парам-ров. Обычно парам-ры неизвестны и приходится находить их оценки (приближенные знач-я). Примером непрерывн. Случ. Вел-ны, распределенной по показательному закону, может служить время между появл-ями двух последовательных соб-й простейшего потока. Показательным наз. распред-е непрер. случ. вел-ны Х к-рое описывается следующей дифференциальной ф-цией

 

Экспоненциальное распред-е для непрер. случ. вел-н явл. аналогом распред-я Пуассона для дискр. случ. вел-н и имеет следующий вид.

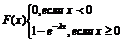
 в-ть попадания случ. вел-ны Х на интервал (α;β)

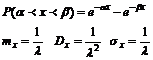
Следует отметить, что время безотказной работы удовлетворяется именно показательному закону, а поэтому это понятие часто исп-ется в понятии надежности.

Числовые хар-ки: пусть непрерывная случ. Вел-на Х распределена по показ. Закону. Найдем МО

 

Интегрируя по частям получим

Таким образом МО показ. Распред-я равно обратной вел-не парам-ра ___. Найдем дисперсию

 

 

Интегрируя по частям получим

 

=>

Найдем ср. квадрат. Отклонение, для чего извлечем квад. Корень из дисперсии:

 

Сравнивая (*) и (**), заключаем, что

Т.е. МО и сред. Квад. Отклонение показ. Распред. Равны.

 

 

2. Критерий согласия Пирсона.

Критерием согласия наз. критерий проверки г-зы о предполагаемом законе неизвестного распред-я.

Описание применения критерия Пирсона к проверке г-зы о нормальном распределении генер. совок-ти. Мы будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении норм. распред-я) частоты. Обычно эти частоты различаются. Случайно ли расхождение частот?

Критерий Пирсона отвечает на поставленный вопрос. Правда, как и любой критерий, он не доказывает справедливость г-зы, а лишь устанавливает на принятом ур-не ее согласие или несогласие с данными наблюдения.

Итак, пусть по выборке объема n получено эмпирическое распред-е:

варианты                                                                                                                                                              х_i   x₁    x₂,,,,,,.x_s

эмп.частоты                                                                                                                                                       n_i                                       n₁                                     n₂.......n_s

Допустим, что в предположении норм. распред-я генер. совок-ти вычислены теоретические частоты n_i’. При ур-не значимости альфа требуется проверить нулевую г-зу: генер. совок-ть распределена нормально.

В кач. критерия проверки нулев. г-зы примем случ. вел-ну

см. стр.330

Число степеней свободы находят по равенству k=s-1-r, где s-число групп (частичных интервалов) выборки, r - число парам-ров предполагаемого распред-я, к-рые оценены по данным выборки.

В частности, если предполагаемое распред-е - нормальное, то оценивают 2 парам-ра (мат.ожидание и ср. квадратическое отклонение), поэтому r=2 и число степеней свободы k=s-1-r=s-1-2=s-3,

Правило. Для того, чтобы при заданом ур-не значимости проверить нулевую г-зу Н₀: генер. совок-ть распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое знач-е критерия:

см.стр331

и по табл. критич. точек распред-я1, по заданному ур-ню значимости альфа и числу степеней свободы k=s-3 найти критич. точку                                            .

Если                                                                            <                                                                                     - нет оснований отвергнуть нулевую г-зу. Если                                                               >                                                                                     - нулевую г-зу отвергают.

==============================================================
Билет 22.

(1) Норм. закон распред-я. Ф-я плот-ти и осн. числовые хар-ки. Нормальным называется распред-е в-тей непрер. случ. вел-ны Х если ф-ция плот-ти распред-я

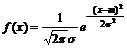
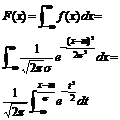
Нормал. Расп-е определяется 2-мя парам-рами:__________ (их достаточно знать, чтобы задать норм. Расп-е). Покажем, что вероятностный смысл этих парам-ров таков: ___есть МО, ___ есть ср. квадр. Отклонение норм. Распр-я. По определению МО непрер. случ. Вел-ны

 

Введем новую переменную __________________. Отсюда ______________ _____________. Приняв по внимание, что новые пределы интегрирования равны старым, получим

 

 

Первое из слагаемых равно нулю (под знаком интеграла нечетная ф-я; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых равно ____ (интеграл Пуассона ____________________). Итак ___________,т.е. МО норм. Распр-я равно парам-ру _____. По определению дисперии непрер. случ. Вел-ны, учитывая, что _________, имеем

 

 

Введем новую переменную ______________. Отсюда ___________ ___________. Приняв во внимание, что новые пределы интегрирования равны старым, получим

 

 

Интегрируя по частям, положив ____________________________ найдем _________

=>

Итак, сред. Квадр. Отклонение норм. распр-я равно парам-ру_______.

Гр-к плот-ти норм. Расп-я наз. норм. кривой (кривой Гаусса). Исследуем ф-ю 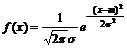 методами дифференциального исчисления. 1) ф-я определена на всей оси х

 

 

2) при всех знач-ях Х ф-я принимает положит. Знач-я, т.е. нормальная кривая расположена над осью ОХ. 3) предел ф-ции при неограниченном возрастании х (по абсолютной вел-не) равен нулю

 

т.е. ось Ох служит горизонтальной асимтотой гр-ка. 4) исследуя ф-ю на экстремум, найдем 1-ю производную

 

Легко видеть, что ________ при х=а _______ при ________, _________ при ____________. =>, при х=а ф-я имеет максимум равный ___________. 5) Разность х-а содержится в аналитическом выражении ф-ции в квадрате, т.е. гр-к ф-ции симметричен относительно прямой х=а. 6) исследуем ф-ю на точки перегиба. Найдем 2-ю производную

 

 

Легко видеть, что при _______________и ______________ вторая производная равна нулю, а при переходе ч-з эти точки она меняет знак (в обеих этих точках знач-е ф-и равно

___________________). Таким образом, точки гр-ка ___________________________ и ______________________ явл. Точками перегиба.