Силой называется векторная величина, определяющая меру механического взаимодействия двух тел.

Силой называется векторная величина, определяющая меру механического взаимодействия двух тел.

Характеристиками действия силы являются:

а) численное значение силы или ее модуль;

б) направление силы;

в) точка ее приложения.

Линией действия силы называется прямая, вдоль которой действует сила.

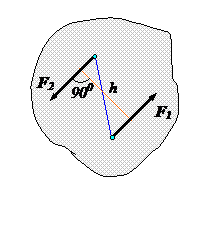
 Парой сил называется совокупность двух равных по модулю, параллельных и противоположно направленных сил.

Момент пары в плоской системе сил определяется как алгебраическая величина, равная взятым со знаком плюс или минус произведению одной из сил пары на плечо.

 

                 

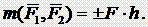
 Плечо пары – кратчайшее расстояние между линиями действия сил пары.

Момент пары имеет знак плюс, если пара стремиться повернуть тело против часовой стрелки.

Сумма проекций сил пары на любую ось равна нулю.

Системой сил называется совокупность сил, приложенных к одному твердому телу.  

Плоской называется система сил, линии действия которых лежат в одной плоскости.

  Связями называются любые ограничения, препятствующие перемещениям тела в пространстве.

К связям относятся различного вида устройства, закрепляющие тела, и опорные поверхности.

Равновесие плоской системы сил

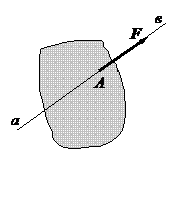
 Моментом силы относительно центра на плоскости называется произведение модуля силы на плечо. Плечо – перпендикуляр, опущенный из центра на линию действия силы.

Момент считается положительным, если сила стремится повернуть тело вокруг выбранного центра против часовой стрелки.

                              ,

                          ,

                          .

 

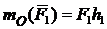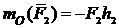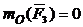Если линия действия силы проходит через центр, то момент силы относительно этого центра равен нулю.

Проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца вектора силы.

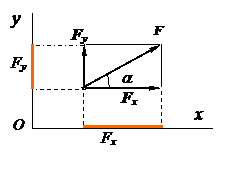Проекция имеет знак плюс, если перемещение от ее начала к концу, происходит в положительном направлении оси, и знак минус – если в отрицательном.

Проекция силы на ось равна произведению силы на косинус угла между направлением силы и положительным направлением оси.

                   

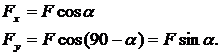
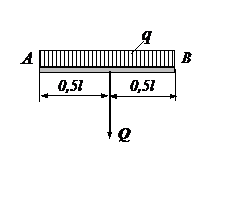Распределенными называются силы, действующие в каждой точке отрезка прямой.

Интенсивностью  называется сила, приходящаяся на единицу длины. Интенсивность обозначается буквой q

Равномерно распределенная нагрузка на участке АВ длиной l и интенсивностью q приводится к равнодействующей силе Q, параллельной действующим силам, приложенной в середине отрезка АВ и равной Q = ql.

Пример решения задачи на равновесие плоской системы сил.

 

Стержень АВ, одним концом закреплен шарнирно, другим опирается на гладкую вертикальную стену. На стержень действует сила Р = 6 кН  и пара сил с моментом М = 20 кНм, АС = СВ =2 м.  

Определить реакции опор.

             

  Решение.

Выбираем оси координат: направляем ось х горизонтально вправо, ось у – вертикально вверх.

  Кроме активных сил, на стержень действуют: реакция подшипника, которую раскладываем на две составляющие: Х_А , У_А , и реакция R _B, направленная перпендикулярно опорной плоскости.

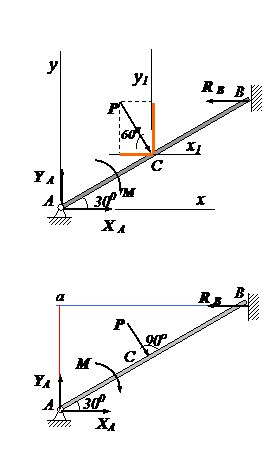Составим уравнения равновесия. Проведем в точке С, где приложена сила Р, прямые, параллельные осям х и у. Проекции силы Р на эти прямые равны соответственно ее проекциям на оси х и у:  

 

    

 

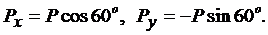
Сумма проекций сил, составляющих пару, на любую ось, равна нулю.

    За центр моментов выбираем точку А, моменты сил Х_А , У_А относительно этой точки равны нулю, сумма моментов сил пары относительно любой точки равна моменту пары. Плечом силы Р является расстояние АС, плечом силы R _B  - перпендикуляр Аа, опущенный из точки А на линию действия этой силы. .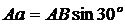

Получаем уравнения равновесия:

 

.

 

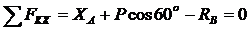
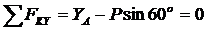
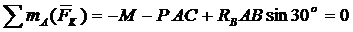Теорема Вариньона. Момент равнодействующей относительно какого-либо центра для плоской системы сил равен алгебраической сумме моментов ее составляющих относительно того же самого центра.

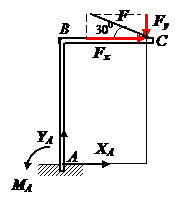
Задача. Определить реакциибалки АВС

Составим уравнения проекций сил на оси координат, учитывая, что проекции сил пары на любую ось равны нулю.

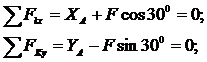                        (1)

Для ого, чтобы определить момент силы F относительно точки А, разложим ее на составляющие

F_x = F cos30⁰ и   F_y = F sin30⁰  и применим теорему о моменте равнодействующей

                       

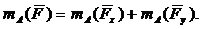
Уравнение моментов всех сил относительно точки

 

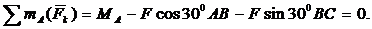                           (2)

Уравнения (1) и (2) определяют реакции жесткой заделки в точке А.

Равновесие пространственной системы сил.

Уравнения равновесия пространственной системы сил.

 

 Для равновесия пространственной системы сил необходимо и достаточно, чтобы три суммы проекций всех сил на оси координат равнялись нулю и три суммы моментов всех сил относительно каждой координатной оси равнялись нулю, т.е. условия равновесия выражаются шестью уравнениями:

 

                                    

 

      

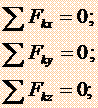
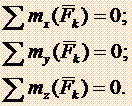
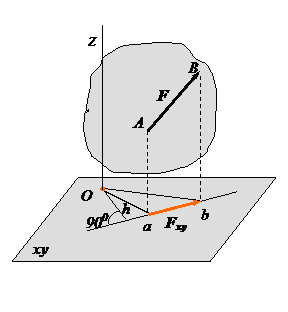  Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную этой оси, относительно точки пересечения оси с плоскостью.

 

Момент силы относительно оси имеет знак плюс, если проекция этой силы на перпендикулярную к оси плоскость, стремится повернуть тело вокруг положительного направления оси против часовой стрелки.   

  

КИНЕМАТИКА

Векторный способ задания движения точки

 

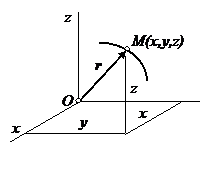Положение точки М в пространстве будет вполне определено, если ее радиус-вектор. проведенный из какого–либо заданного центра О, известен как функция времени, т.е. если  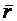является векторной функцией скалярного аргумента t.

Уравнением движения точки называется зависимость радиуса - вектора от времени:

                                              

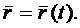
Годографом называется геометрическое место точек концов переменного вектора, отложенного из одной и той же точки.

Таким образом, траекторией точки при векторном способе задания является годограф радиуса - вектора этой точки.

Основные понятия векторного способа задания движения точки.

1. Положение точки в пространстве будет однозначно определено, если будет известен как функция времени ее радиус-вектор, проводимый из неподвижного центра.

                                

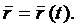
2. Траекторией точки является годограф радиуса-вектора.

3. Скоростью точки называется векторная производная от вектора скорости по времени.

                              

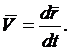
4. Ускорением точки называется векторная производная от вектора-скорости по времени.

                             

    

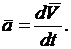
 Координатный способ задания движения точки

 

 Положение точки в пространстве относительно выбранной системы координат определяется координатами x, y, z.

Уравнения движения точки представляют собой зависимость координат движущейся точки от времени:

              

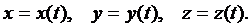
Траектория точки. Уравнения движения точки представляют собой одновременно уравнения траектории точки в параметрической форме, где роль параметра играет время t.

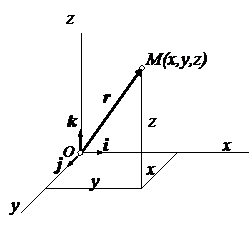Для того, чтобы получить выражение траектории в координатной форме, необходимо каким-то образом исключить из уравнений движения время t.

Значения проекций скорости на оси координат: 

                   

 

 

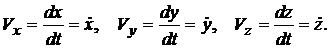
Модуль вектора скорости равен

                   .                                            

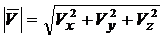  Направление вектора скорости определяется направляющими косинусами углов, которые вектор скорости образует с координатными осями: 

                   

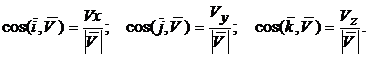
Значения проекций вектора ускорения на оси координат:

 

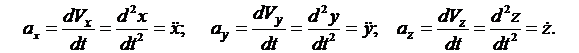(1.7)

 

Модуль ускорения  

                                                                 

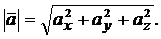
Направляющие косинусы вектора ускорения равны

            

 

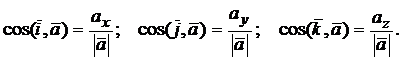
 Естественный способ задания движения точки.

  Этот способ применяется в том случае, когда траектория, по которой движется точка, известна.

  Выберем на траектории фиксированную точку О и направление положительного отсчета дуги.

Положение точки М в любой момент времени будет определяться значением дуговой координаты S = OM, отсчитываемой от точки О.

Законом движения точки называется зависимость дуговой координаты от времени:

                                      .                              

Проекция 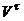вектора скорости точки на касательную равна производной от дуговой координаты по времени.

                                .                             

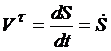Вектор ускорения равен геометрической сумме векторов, один из которых 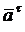 направлен по касательной, а другой 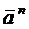- по главной нормали.

Проекция ускорения на 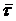называется касательным ускорением

       .               

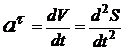Примером плоскопараллельного движения может служить движение цилиндра по горизонтальной плоскости, при котором его основание остается параллельным вертикальной плоскости.

           Основная теорема

Мгновенный центр скоростей

Задачи

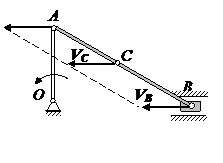
Задача 1. Найти скорости точек А, В и D обода колеса, катящегося по прямолинейному рельсу без скольжения, если скорость центра колеса С равна V_C. Определить скорости точек А, В, D и угловую скорость колеса.

Решение. Мгновенный центр скоростей Р колеса находится в точке контакта колеса с неподвижной плоскостью. Скорости точек А, В, D перпендикулярны к отрезкам, соединяющим эти точкис точкой Р, модули скоростей пропорциональны их длинам:

           

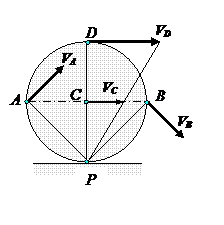
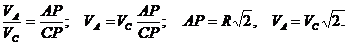
Расстояния точек А и В до мгновенного центра скоростей одинаковы, следовательно, скорости этих точек равны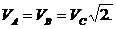

Скорость точки D   равна   2 V _C, так как расстояние точки D  до мгновенного центра скоростей в два раза больше расстояния СР.

Угловая скорость колеса равна  

                                                     

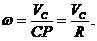
Задача.2. Диск зажат между двумя рейками, которые движутся со скоростями V ₁ и V ₂ (V ₁ > V ₂).

Определить угловую скорость диска и скорость его центра, если его радиус равен R.

Скорость точки А диска равна скорости верхней рейки, а скорость точки В – скорости нижней рейки. Мгновенный центр скоростей находится в точке Р. Скорость точки С является средней линией трапеции ВАав:

                 

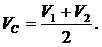
Угловая скорость  

    

 

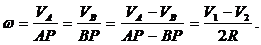
Задача 3. Кривошипно-шатунный механизм

1. Рассмотрим произвольное положение механизма. Угловая скорость кривошипа равна ω_ОА.  Определить угловую скорость шатуна и скорости точек А,В, и С для трех положений механизма.

Решение. Кривошип ОА вращается вокруг точки О, шатун АВ совершает плоское движение в плоскости чертежа. Во всех случаях скорость точки А перпендикулярна кривошипу и равна 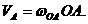, а скорость точки В направлена по горизонтальной прямой.

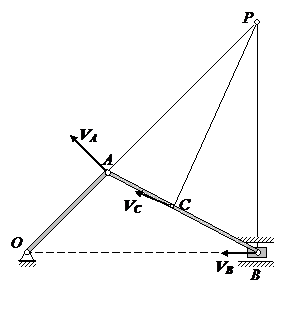Кривошип ОА образует острый угол с горизонтальной прямой. Мгновенный центр скоростей шатуна находится в точке Р, где пересекаются восстановленные в точках А и В перпендикуляры к скоростям в этих точках.

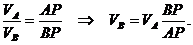
Скорость точки С направлена перпендикулярно отрезку РС и находится из пропорции: 

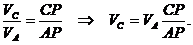
Угловая скорость шатуна равна

                                                           

 

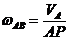
2. Кривошип и шатун расположены на однойпрямой

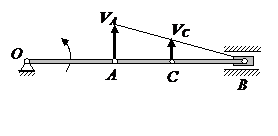В этом положении мгновенный центр скоростей находится в точке В, поэтому скорость V_B равна нулю.

Скорость точки С находится из пропорции:

          

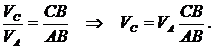
Угловая скорость шатуна равна

          

 

 

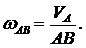
3. Кривошип занимает вертикальное положение. В этом случае мгновенный центр скоростей шатуна находится в бесконечности, скорости всех его точек равны, угловая скорость шатуна равна нулю.

 

 План скоростей

План скоростей представляет собой графический метод определения скоростей точек плоской фигуры. Для его построения необходимо знать модуль и направление одной точки плоской фигуры и направление скорости другой точки.

Пусть известны вектор скорости точки А и направление скорости точки В. Определить модуль скорости точки В.

Скорость точки В определяется формулой

         .

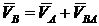В этой формуле известны направление и модуль скорости точки А, направление скорости точки В и направление скорости 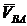, так как .

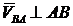Выбираем произвольный центр О и в произвольно выбранном масштабе откладываем вектор 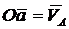. Из этой же точки поводим прямую, параллельную скорости 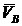точки В (рис. а), затем из точки а проводим прямую, параллельную скорости 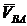, т.е. перпендикулярно отрезку АВ. Точка пересечения прямых, одна из которых параллельна 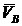, другая - 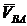, определяет точку в, полученный вектор  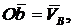а вектор 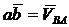.(рис. б)

 

 

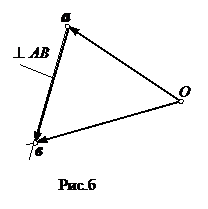Определим на плане скоростей модуль и направление скорости точки С. Выбираем за полюс точку А, тогда 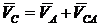. Если бы была известна скорость 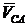, то, отложив от точки а вектор 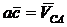, получили бы вектор  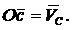Но известно только направление этого вектора 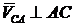, поэтому учтем, что конец вектора  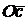на плане скоростей (б) лежит на прямой, проведенной из точки а перпендикулярно АС.

С другой стороны, 

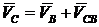    , где .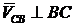

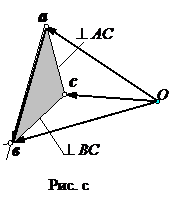
 Это означает, что конец вектора 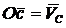  (рис. с.) должен находится на прямой, проведенной через точку в перпендикулярно отрезку ВС.

Таким образом, конец скорости 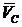  находится в точке с пересечения прямых, перпендикулярных к отрезкам АС и ВС, т.е. на плане скоростей 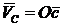. Как следует из построения, треугольники АВС и авс подобны и повернуты друг относительно друга на угол 90⁰.

 

Задача. Определить скорости точек В и С шатуна кривошипно-шатунного механизма (рис. а)  путем построения плана скоростей, если известно, что угловая скорость кривошипа ОА равна ω и АС = СВ.

Построение плана скоростей.

Скорость точки А перпендикулярна кривошипу и равна

   V_A = ω OA.

  Скорость 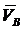точки В направлена горизонтально влево.

, .

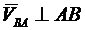Выберем полюс (б)и отложим из него в выбранном масштабе вектор 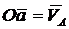. (рис.б). Из этого же полюса проведем прямую, параллельную вектору 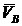. Затем из конца вектора  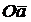поведем прямую, перпендикулярную шатуну АВ. Точка пересечения этой прямой и прямой, параллельной 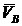, определяет конец вектора .

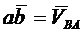Аналогично, , .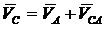

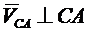Кроме того,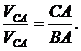

Для того, чтобы определить вектор 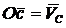, разделим на плане скоростей отрезок ав пополам, полученную точку с соединим с точкой О вектором .

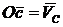 Ускорения точек плоской фигуры.

Движение плоской фигуры в своей плоскости можно разложить на поступательное движение вместе с произвольно выбранной точкой, принимаемой за полюс, и вращательное движение вокруг этого полюса.

Следовательно, ускорение любой точки при плоском движении равно геометрической сумме двух ускорений: ускорения выбранного полюса, и ускорения, полученного данной точкой при ее вращательном движении вокруг полюса.

Пусть известно ускорение точки А плоской фигуры тогда ускорение другой точки этой фигуры будет равно

                        ,

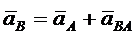где ускорение вращательного движения точки А вокруг точки В раскладывается на нормальное и касательное ускорения:

              

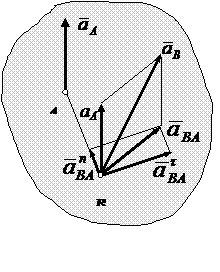
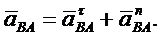
Касательное ускорение вращательного движения точки вокруг полюса направлено перпендикулярно отрезку АВ, соединяющему точку В с полюсом А, и равно 

                   

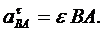
Нормальное ускорение направлено по отрезку ВА к полюсу А и равно

                   

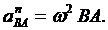
Окончательно, полное ускорение точки В равно геометрической сумме трех ускорений: ускорения выбранного полюса А, нормального и касательного ускорений вращательного движения точки В вокруг этого полюса:

План ускорений

Ускорения точек плоской фигуры могут быть определены графически с помощью плана ускорений. Этот метод позволяет находить ускорение точки плоской фигуры при условии, что известна траектория этой точки, ее скорость и ускорение одной из точек этой фигуры.

Пусть известно ускорение 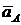 точки А плоской фигуры, скорость  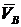точки В  и ее траектория векторы на нем изображены без соблюдения масштабов).

   Так как точка В совершает криволинейное движение, то ее ускорение раскладывается на нормальную и касательную составляющие:

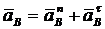         .         (а)  

 

Оба ускорения известны по направлениям, ускорение 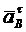 направлено по касательной к траектории движения точки В,  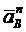 - по главной нормали.

Модуль нормального ускорения определяется по формуле для криволинейного движения

                ,

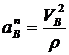где ρ – радиус кривизны траектории в данной точке.

 Модуль касательного ускорения не определяется, так как закон движения точки В не задан. Следовательно, на основе анализа криволинейного движения полное ускорение точки найти не удается.

   Проведем анализ плоского движения твердого тела, которому принадлежит точка В.

   Плоское движение можно представить как сумму двух движений: поступательного вместе с точкой А и вращательного вокруг этой точки. В этом случае ускорение точки В выражается через ускорение точки А, модуль и направление которого известны, т.е.

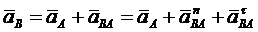             ,                           (б)                        

где 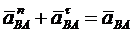 и является полным ускорением точки В во вращательном движении плоской фигуры вокруг точки А.   

В равенстве (б) все составляющие ускорения точки В известны по направлению. Ускорение точки А задано, ускорение 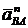 направлено по прямой ВА  к точке А, касательное ускорение  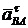- перпендикулярно прямой ВА.

Модуль ускорения 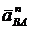 определяется по формуле вращательного движения точки В вокруг точки А

          ,

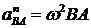где ω  - угловая скорость плоской фигуры, ВА - радиус вращения.

Касательное ускорение 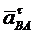 по величине не определено.

Приравняем правые части выражений (а) и (б).

Для графического определения ускорения точки В используем выражения (а) и (б).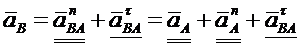                        

В этом равенстве одной чертой подчеркнуты векторы, у которых известно только направление, двумя чертами – векторы, для которых известны и направление и модуль. 

 Выберем неподвижную точку О за полюс и масштаб, в котором будем откладывать векторы ускорений. Отложим из точки О вектор 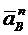 и проведем к нему под прямым углом прямую, которая соответствует направлению вектора .

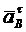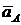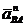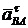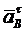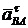Из этой же точки О отложим вектор . Из конца этого вектора отложим вектор  и проведем к нему перпендикулярную прямую, которая определяет направление вектора . Точка в пересечения прямых, соответствующих направлениям векторов и , определяет конец вектора 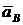. Соединим точки О и в (рис. 3.43) и получим в выбранном масштабе ускорение точки В.

 Так как 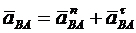, то, соединив, на графике точки а и в  получим  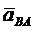полное ускорение вращательного движения точки В вокруг точки А.

Определим на графике ускорение точки С, которая делит расстояние между точками А и в пополам.  Ускорение этой точки также можно выразить через ускорение точки А:

                  .

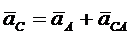Ускорения точек при вращательном движении пропорциональны радиусам вращения, поэтому

                         .

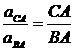Следовательно, для того, чтобы получить ускорение 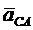, достаточно на графике разделить расстояние ав пополам, полученную точку обозначим буквой с. Отрезок ас определяет величину ускорения 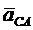. Соединяя точку с с точкой О получим на графике ускорение точки С плоской фигуры.

 

  Задача. Построим план ускорений для механизма, в положении, указанном на рис. 3.45, если кривошип ОА вращается с постоянной угловой скоростью ω = 2 1/с, ОА = ВА =0,6м, СВ = 0,3 м, φ = 30⁰.     

  Решение. П ри равномерном вращении кривошипа касательное ускорение точки А будет равно нулю, поэтому полное ускорение равно нормальному ускорению,

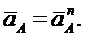
Вектор нормального ускорения направлен вдоль АО и равен

                       

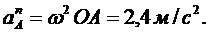
Ускорение точки В равно

                         . (а)

Ускорение точки В направлено горизонтально, так как ползун движется в горизонтальный направляющих, ускорение 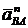 направлено к точке по прямой АВ, и равно

                                  ,

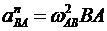где ω_АВ - угловая скорость шатуна АВ.

Угловую скорость звена АВ можно определить с помощью мгновенного центра скоростей который находится в точке Р пересечения перпендикуляров к скоростям в точках А и В.  

  

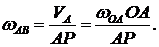
Из треугольника ОАВ АВ = ОА tg 60⁰,

Из треугольника АВР:

АР = АВ tq 60⁰ = OA tq ² 60⁰ =1,8 м.

Тогда

     

    .

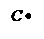
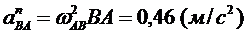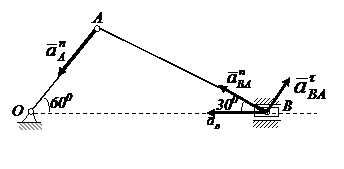Таким образом, в равенстве (а) векторы  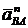и  и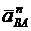звестны по модулю и направлению, ускорения 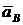и 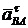 только по направлению. Ускорение  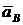направлено вдоль направляющих, ограничивающих движение ползуна, ускорение  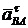- перпендикулярно АВ

Используя все полученные значения, строим план ускорений Выберем неподвижную точку О за начало ускорений всех точек звена АВ и установим масштаб для изображения ускорений. Проведем из точки О прямую, параллельную вектору 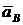. Отложим из этой же точки вектор 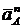, конец которого обозначим буквой а. Из точки а отложим вектор  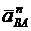(проведем прямую параллельную АВ), из конца этого вектора проведем прямую, параллельную вектору  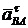(перпендикулярно отрезку АВ) и продолжим ее до пересечения с направлением вектора 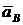. Полученную точку пересечения обозначим буквой в. Соединим точку О с точкой в, полученный отрезок OB в выбранном масштабе является ускорением 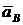точки В. Соединим точки а и в, полученный отрезок ав  в выбранном масштабе представляет собой полное ускорение вращательного движения  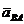точки В вокруг точки А.

Для того, чтобы определить ускорение любой точки D шатуна АВ, следует отрезок ав, представляющий собой вращательное ускорение точки В вокруг точки А, разделить точкой d в пропорции:

                               .

Соединив точку d с точкой О, получим ускорение точки D шатуна АВ. Например, если AD = 0,25 AB, то, отложив из точки а отрезок ad = 0,25 ab, получим на графике точку d. Значит, отрезок О d в выбранном масштабе является ускорением точки D шатуна.

 

                  

Силой называется векторная величина, определяющая меру механического взаимодействия двух тел.

Характеристиками действия силы являются:

а) численное значение силы или ее модуль;

б) направление силы;

в) точка ее приложения.