Многожидкостный режим течения характерен для смесей молекулярных газов или жидкостей с большим различием масс молекул (и/или эффективных сечений рассеяния молекул). Этот режим течения типичен и для дисперсных жидкостей, газовзвесей, суспензий, эмульсий, аэрозолей. Как уже отмечалось, динамика многожидкостной гетерогенной системы описывается набором парциальных плотностей  , скоростей
, скоростей 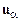 и энергий
и энергий 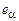 . Уравнения переноса для парциальных макроскопических переменных получаются так же, как для однокомпонентной системы, обычным образом как следствие выполнения законов сохранения массы, импульса и энергии всей системы и их локального сохранения внутри компонента. Если в системе отсутствуют фазовые переходы, химические реакции и другие процессы, приводящие к изменению состава, то эти уравнения имеют вид
. Уравнения переноса для парциальных макроскопических переменных получаются так же, как для однокомпонентной системы, обычным образом как следствие выполнения законов сохранения массы, импульса и энергии всей системы и их локального сохранения внутри компонента. Если в системе отсутствуют фазовые переходы, химические реакции и другие процессы, приводящие к изменению состава, то эти уравнения имеют вид
 ,
,  ,
,
 ,
,
 , (16.1)
, (16.1)
где  – сила межфазного взаимодействия, а
– сила межфазного взаимодействия, а 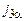 – производство энергии, обусловленное межкомпонентным взаимодействием.
– производство энергии, обусловленное межкомпонентным взаимодействием.  – вектор массовых сил, действующих на компонент
– вектор массовых сил, действующих на компонент  .
.
В уравнениях (16.1) снова необходимо задать определяющие соотношения, вывод которых для гетерогенных систем осложняется именно неоднородностью их состава. При исследовании характера деформирования некоторого выделенного объема смеси необходимо учесть реакции, связанные не только со смещением внешней границы объема, как обычно делается при выводе уравнений Навье – Стокса, но и со смещениями межфазных границ. Столь же не просто определить силы межфазного взаимодействия. Ситуация однако существенно упрощается, если, как это имеет место в газовзвесях и суспензиях, межфазная граница не меняет свою форму. Именно такие системы мы в дальнейшем и будем анализировать.
Определяющие соотношения
Наиболее последовательным феноменологическим методом получения определяющих соотношений для уравнений многожидкостной гидродинамики является их вывод с помощью термодинамики необратимых процессов. В этом случае удается получить полный набор определяющих соотношений для тензора напряжений, векторов потока тепла и диффузии и для межфазных сил и эти соотношения имеют вид
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,

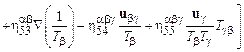 , (16.2)
, (16.2)
Определяющие соотношения (16.2) получены в предположении линейности потоков по термодинамическим силам (градиентам макроскопических переменных). Это в свою очередь требует, чтобы термодинамические силы, связанные с градиентами макроскопических величин, были одного порядка величины с термодинамическими силами, обусловленными различием скоростей и температур между компонентами. в дальнейшем величины 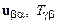 будем называть просто диффузионными скоростями и температурами. Конечно, в общем случае диффузионные скорости и температуры могут быть одного порядка величинами со скоростями и температурами компонентов смеси. Тогда соотношения (16.2) уже не применимы, однако методы термодинамики необратимых процессов и неравновесная статистической механики и в этом случае позволяют построить определяющие соотношения.
будем называть просто диффузионными скоростями и температурами. Конечно, в общем случае диффузионные скорости и температуры могут быть одного порядка величинами со скоростями и температурами компонентов смеси. Тогда соотношения (16.2) уже не применимы, однако методы термодинамики необратимых процессов и неравновесная статистической механики и в этом случае позволяют построить определяющие соотношения.
Методы осреднения
Термодинамика необратимых процессов достаточно просто позволяет получить определяющие соотношения для уравнений многожидкостной гидродинамики. Недостатком этого метода является его достоинство: чрезвычайная общность. При таком подходе не удается учесть и изучить тонкие эффекты взаимодействия сред на межфазных границах, возможные флуктуационные процессы. В связи с этим для вывода определяющих соотношений и уравнений широко используются, как мы уже отмечали, различные методы осреднения: осреднение по пространству, по времени, по некоторому статистическому ансамблю. Иногда методы осреднения сочетаются с применением термодинамики неравновесных процессов или принципов так называемой рациональной механики. Проанализируем, чего удается достичь при использовании методов усреднения.
Схема применения метода осреднения по объему ясно изложена в монографиях Р.И. Нигматулина, несколько иной пример можно найти в серии работ Д. Дрю. Для простоты в этом разделе мы будем говорить о двухфазной среде. Итак, пусть рассматриваемая двухфазная система занимает объем 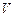 , ограниченный поверхностью
, ограниченный поверхностью  . Каждая из фаз занимает объем
. Каждая из фаз занимает объем  ,
,  – объем, занятый несущей средой, а
– объем, занятый несущей средой, а 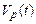 – объем, занятый дисперсной фазой, а
– объем, занятый дисперсной фазой, а  . Соответственно часть граничной поверхности
. Соответственно часть граничной поверхности 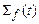 проходит через первую фазу, а
проходит через первую фазу, а 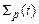 – через вторую,
– через вторую,  . Обычно считается, что несущая среда является топологически связной, а дисперсная нет. Таким образом, в объеме
. Обычно считается, что несущая среда является топологически связной, а дисперсная нет. Таким образом, в объеме 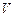 имеется в общем случае многосвязная межфазная поверхность
имеется в общем случае многосвязная межфазная поверхность 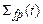 . Предполагается, что внутри объема, занимаемого фазой
. Предполагается, что внутри объема, занимаемого фазой  , справедливы уравнения однофазной гидромеханики
, справедливы уравнения однофазной гидромеханики
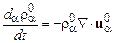 ,
,  ,
,
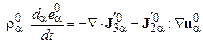 ,
,  , (16.3)
, (16.3)
где 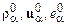 – плотность, скорость и внутренняя энергия компонента
– плотность, скорость и внутренняя энергия компонента  , отнесенные к объему
, отнесенные к объему  . Эти величины называют «микроскопическими».
. Эти величины называют «микроскопическими». 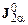 ,
,  – соответствующие значения тензора напряжений и вектора потока тепла. Система уравнений (16.3) замыкается уравнениями состояния фаз и их определяющими соотношениями. Обычно предполагается, что фазы представляют собой ньютоновские жидкости, т. е.
– соответствующие значения тензора напряжений и вектора потока тепла. Система уравнений (16.3) замыкается уравнениями состояния фаз и их определяющими соотношениями. Обычно предполагается, что фазы представляют собой ньютоновские жидкости, т. е.
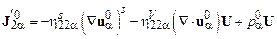
,
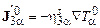 ,
, 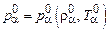 . (16.4)
. (16.4)
Затем вводятся собственно макроскопические переменные, 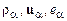 , которые получаются из
, которые получаются из 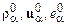 усреднением по физически бесконечно малому объему
усреднением по физически бесконечно малому объему  . В результате осреднения уравнений (16.3) получаются уравнения для переменных
. В результате осреднения уравнений (16.3) получаются уравнения для переменных 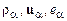 , которые содержат члены, ответственные за межфазные взаимодействия, удается также конкретизировать выражения для тензора напряжений и вектора потока тепла. Неприятность, однако, состоит в том, что, как и следовало ожидать, получающиеся в результате осреднения уравнения переноса гетерогенной среды оказываются незамкнутыми. Они содержат корреляционные составляющие напряжений и вектора потока тепла. Это типичная проблема, возникающая при переходе к огрубленным переменным. Совершенно такая же проблема появляется в теории турбулентности при выводе так называемых уравнений Рейнольдса. Попытка решить ее, записав уравнения для пульсационных составляющих напряжений, как правило, не спасает положения, поскольку в получающихся при этом уравнениях появляются неизвестные члены, связанные с корреляциями более высокого порядка. На этом пути мы приходим к бесконечной цепочке уравнений для макроскопических переменных и корреляционных тензоров, составляющими в которых являются флуктуирующие величины
, которые содержат члены, ответственные за межфазные взаимодействия, удается также конкретизировать выражения для тензора напряжений и вектора потока тепла. Неприятность, однако, состоит в том, что, как и следовало ожидать, получающиеся в результате осреднения уравнения переноса гетерогенной среды оказываются незамкнутыми. Они содержат корреляционные составляющие напряжений и вектора потока тепла. Это типичная проблема, возникающая при переходе к огрубленным переменным. Совершенно такая же проблема появляется в теории турбулентности при выводе так называемых уравнений Рейнольдса. Попытка решить ее, записав уравнения для пульсационных составляющих напряжений, как правило, не спасает положения, поскольку в получающихся при этом уравнениях появляются неизвестные члены, связанные с корреляциями более высокого порядка. На этом пути мы приходим к бесконечной цепочке уравнений для макроскопических переменных и корреляционных тензоров, составляющими в которых являются флуктуирующие величины
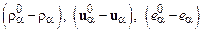 .
.
Однако даже вывод подобной цепочки в механике многофазных сред является нерешенной задачей.
Обычно при использовании методов осреднения решить проблему замыкания уравнений гидромеханики пытаются уже на уровне корреляционных моментов второго порядка. Общепринятых схем такого замыкания нет, да и их появления трудно ожидать. Нельзя надеяться на универсальность поведения корреляционных составляющих тензоров напряжений для гетерогенных систем различной физической природы, с разными начальными и граничными условиями, для разных течений. Утверждение о том, что в разреженной гетерогенной среде при малых скоростях относительного движения фаз вклад корреляционных напряжений в уравнения переноса мал, и хотя кажется в ряде случаев правдоподобным, является не более чем гипотезой. Проблема замыкания наиболее остро стоит в гидродинамических течениях, где эффекты вязкости принципиальны. Именно здесь все еще нельзя говорить о создании достаточно апробированных моделей. Напротив, в газодинамических течениях с большой долей уверенности можно утверждать, что существующие феноменологические модели описывают широкий класс сред и течений, хотя произвол в определении сил межфазного взаимодействия и различных констант все еще слишком велик.
Тем не менее, если пренебречь вкладами появляющихся в уравнениях корреляционных составляющих напряжений, потока тепла и других параметров, и считать, что определяющие соотношения «микроскопических» уравнений переноса являются ньютоновскими, то для дисперсных жидкостей получаются следующие уравнения неразрывности и переноса импульса[45]:
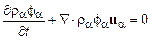 ,
,
 , (16.5)
, (16.5)
где тензор напряжений задается соотношением
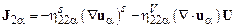
,
в котором в качестве коэффициентов переноса для несущей фазы выбираются некоторые эффективные коэффициенты вязкости. Отличительной особенностью уравнений (16.5) является появление весовых множителей, объемных концентраций фаз 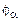 . Их появление связано с усреднением уравнений. Кроме того, в этих уравнениях фигурируют общее давление и, вообще говоря, общий тензор напряжений. В этом смысле можно говорить, что в результате усреднения мы получаем уравнения некоторой квазиоднородной среды с общим давлением и напряжениями.
. Их появление связано с усреднением уравнений. Кроме того, в этих уравнениях фигурируют общее давление и, вообще говоря, общий тензор напряжений. В этом смысле можно говорить, что в результате усреднения мы получаем уравнения некоторой квазиоднородной среды с общим давлением и напряжениями.
Разнообразие тел природы, обусловленное
различием материалов, из которых образо-
ваны эти тела, отражено в теории опреде-
ляющих соотношений.
Клиффорд Трусделл
Определяющие соотношения
Неньютоновских жидкостей
Нелинейно-вязкие жидкости
Жидкости, для которых определяющие соотношения имеют вид (12.15), (12.16), называются ньютоновскими. Поведение многих жидкостей, однако, радикально отличается от ньютоновских. Так, эксперименты с полимерными жидкостями, например, фиксируют существенное изменение коэффициента вязкости среды (уменьшение на несколько порядков) при возрастании градиента скорости. Известны и другие весьма экзотические свойства, наблюдаемые экспериментально во многих жидкостях. Чтобы познакомиться с известными и наиболее распространенными моделями неньютоновских жидкостей, рассмотрим сначала случай несжимаемых жидкостей, поле скорости которых является соленоидальным
 . (17.1)
. (17.1)
Реологическое уравнение (12.15) в этом случае существенно упрощается
 , (17.2)
, (17.2)
где введен тензор скоростей деформации 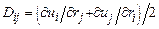 .
.
Важнейшим исходным посылом при формулировании моделей определяющих соотношений широкого класса неньютоновских жидкостей служит постулат Стокса, согласно которому тензор напряжений является непрерывной функцией тензора скоростей деформаций
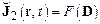 . (17.3)
. (17.3)
Обычно при определении реологических соотношений тензор напряжений предполагают все также линейным относительно тензора скоростей деформации, одновременно считая, что коэффициент вязкости является некоторой функцией градиентов скорости. В частности, реологическое уравнение для так называемой жидкости Стокса задается соотношением
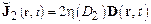 . (17.4)
. (17.4)
где  – второй инвариант тензора скоростей деформации[46].
– второй инвариант тензора скоростей деформации[46].
Заметим, что нелинейно-вязкие жидкости типа (17.4) можно ввести и для сжимаемых жидкостей. В этом случае возникают однако некоторые проблемы с определением давления. В книге В.Г. Литвинова для этой цели предлагается использовать реологическое уравнение
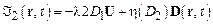 . (17.5)
. (17.5)
где 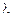 – положительная константа, а
– положительная константа, а 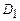 – первый инвариант тензора скоростей деформации. Роль давления здесь играет комплекс
– первый инвариант тензора скоростей деформации. Роль давления здесь играет комплекс 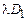 .
.
Реологическое соотношение (17.4) определяет широкий класс жидкостей (в том числе и ньютоновских) с весьма различными свойствами. Чтобы классифицировать их, рассмотрим частный случай плоского сдвигового течения (течения Куэтта) между двумя бесконечными параллельными пластинами, одна из которых неподвижна, а вторая движется с заданной скоростью. Пусть течение происходит вдоль оси  со скоростью
со скоростью 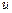 , а пластины перпендикулярны оси
, а пластины перпендикулярны оси 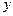 . Для ньютоновских жидкостей течение это характеризуется линейным профилем скорости
. Для ньютоновских жидкостей течение это характеризуется линейным профилем скорости 

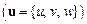 , где параметр
, где параметр 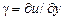 задает величину скорости сдвига. Тензор напряжений имеет в этом случае две ненулевые составляющие
задает величину скорости сдвига. Тензор напряжений имеет в этом случае две ненулевые составляющие
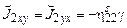 . (17.6)
. (17.6)
Для нелинейно-вязких жидкостей тензор напряжений в течении Куэтта уже не является линейной функцией величины скорости сдвига. Можно выделить два типа жидкостей: дилатантные, для которых
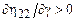 , (17.7)
, (17.7)
и псевдопластические
 . (17.8)
. (17.8)
Ньютоновские жидкости, где  , разделяют их.
, разделяют их.
Псевдопластическими являются, как правило, расплавы и растворы полимеров, а дилатантными – концентрированные суспензии. Наконец, можно выделить вязкопластичные среды, течение которых начинается лишь по достижении некоторого порогового значения напряжений.
Коэффициент переноса 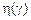 называют кажущейся вязкостью. Эта вязкость, однако, вполне наблюдаемая и определяется отношением
называют кажущейся вязкостью. Эта вязкость, однако, вполне наблюдаемая и определяется отношением 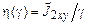 . Так, например, эксперименты показывают, что для псевдопластических жидкостей кажущаяся вязкость с увеличением скорости сдвига остается постоянной, затем уменьшается, а потом выходит на асимптоту (рис. 17.1).
. Так, например, эксперименты показывают, что для псевдопластических жидкостей кажущаяся вязкость с увеличением скорости сдвига остается постоянной, затем уменьшается, а потом выходит на асимптоту (рис. 17.1).
Наряду с жидкостями Стокса (17.4) выделяют жидкости Рейнера – Ривлина, реологическое уравнение которых уже нелинейно относительно тензора скоростей деформаций
 , (17.9)
, (17.9)
где 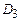 – третий инвариант тензора скоростей деформации, а функцию
– третий инвариант тензора скоростей деформации, а функцию 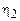 называют поперечной вязкостью.
называют поперечной вязкостью.
Рис. 17.1. Зависимость вязкости от скорости сдвига для
псевдопластической жидкости
Наконец стоит отметить, что существуют жидкости, реологические свойства которых зависят не только от скорости сдвига, но и от продолжительности деформирования. Коль скоро для них важен период деформирования, становится принципиальной сама предыстория течения. Реологические уравнения подобных жидкостей должны быть нелокальными по времени. Временную нелокальность определяющих соотношений мы обсудим в следующем разделе.
Вякоупругие жидкости
Все определяющие соотношения, обсуждавшиеся в двух предыдущих разделах, имеют одну общую черту: эти уравнения локальны и по времени, и по пространству. Это, в частности, означает, что поток (например, тензор напряжения) мгновенно реагирует на изменение соответствующей термодинамической силы (градиента скорости). Среды, для которых такие определяющие соотношения справедливы, соответствуют, по выражению
А. Лоджа чисто вязкой или неупругой жидкости, т. е. жидкости, у которой отсутствует зависимость напряжений от предыстории течения. Ясно, что в реальных жидкостях всегда имеется некоторый конечный (хотя может быть и достаточно малый) релаксационный период реакции потока на изменение соответствующего градиента макроскопической переменной. Если этот процесс достаточно быстрый, его можно пытаться описать обычной экспонентой. В этом случае эволюция тензора напряжений должна была бы задаваться релаксационным уравнением
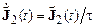 ,
,
где  – некоторое время релаксации. Это уравнение описывает релаксацию напряжения от заданного начального значения
– некоторое время релаксации. Это уравнение описывает релаксацию напряжения от заданного начального значения 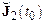 до нуля[47]. Однако, например, в ньютоновских жидкостях напряжения должны приобретать вид (12.16), и мы приходим к уравнению Максвелла[48]
до нуля[47]. Однако, например, в ньютоновских жидкостях напряжения должны приобретать вид (12.16), и мы приходим к уравнению Максвелла[48]
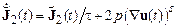 . (17.10)
. (17.10)
Интегрируя это уравнение по времени, находим
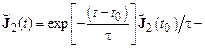
 (17.11)
(17.11)
Если 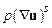 не изменяется заметным образом на временах
не изменяется заметным образом на временах  , то соотношение (17.11) сводится к такому:
, то соотношение (17.11) сводится к такому:
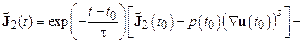
 . (17.12)
. (17.12)
В этом случае на временах порядка  затухает начальная информация не только о тензоре напряжений, но и о тензоре скоростей деформации и на временах
затухает начальная информация не только о тензоре напряжений, но и о тензоре скоростей деформации и на временах  мы имеем обычные ньютоновские определяющие соотношения.
мы имеем обычные ньютоновские определяющие соотношения.
Можно сформулировать и обобщенную релаксационную модель, в которой учитываются временные производные более высоких порядков. Наиболее общей из них будет такая:
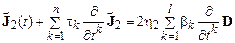 . (17.13)
. (17.13)
Здесь 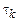 – набор времен релаксации, а
– набор времен релаксации, а  – некоторые посто-янные.
– некоторые посто-янные.
Обычно порядок производной в правой части должен быть ниже, чем производной от тензора напряжений. Предлагались, однако, и модели, где 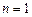 . Недостатки подобных моделей очевидны, эти модели содержат большое число параметров, часть из которых просто ненаблюдаемые. Кроме того, они включают временные производные от тензоров напряжений и скоростей деформаций высших порядков, а это, вообще говоря, требует учета всех нелинейных членов в тензоре напряжений. Подобные нелинейные определяющие соотношения будут обсуждаться в следующем разделе.
. Недостатки подобных моделей очевидны, эти модели содержат большое число параметров, часть из которых просто ненаблюдаемые. Кроме того, они включают временные производные от тензоров напряжений и скоростей деформаций высших порядков, а это, вообще говоря, требует учета всех нелинейных членов в тензоре напряжений. Подобные нелинейные определяющие соотношения будут обсуждаться в следующем разделе.
Жидкость, реологическое уравнение которой имеет вид (17.10), уже не вполне чисто вязкая. Подобная жидкость является типичным представителем так называемых сред с затухающей памятью, упругие свойства здесь проявляются лишь на определенных временах. Существуют, однако, среды, сочетающие упругие и вязкие свойства в значительно большей степени. Приведем здесь в качестве примера определяющие соотношения среды Фойхта, получаемые суперпозицией определяющих соотношений вязкой и упругой сред,
 (17.14)
(17.14)
и определяющие соотношения вязкоупругих сред
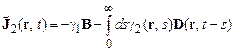 . (17.15)
. (17.15)
Здесь 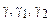 – некоторые постоянные (
– некоторые постоянные (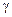 – модуль сдвига), а
– модуль сдвига), а
 – тензор деформаций.
– тензор деформаций.



 , скоростей
, скоростей 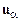 и энергий
и энергий 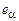 . Уравнения переноса для парциальных макроскопических переменных получаются так же, как для однокомпонентной системы, обычным образом как следствие выполнения законов сохранения массы, импульса и энергии всей системы и их локального сохранения внутри компонента. Если в системе отсутствуют фазовые переходы, химические реакции и другие процессы, приводящие к изменению состава, то эти уравнения имеют вид
. Уравнения переноса для парциальных макроскопических переменных получаются так же, как для однокомпонентной системы, обычным образом как следствие выполнения законов сохранения массы, импульса и энергии всей системы и их локального сохранения внутри компонента. Если в системе отсутствуют фазовые переходы, химические реакции и другие процессы, приводящие к изменению состава, то эти уравнения имеют вид ,
,  ,
, ,
, , (16.1)
, (16.1) – сила межфазного взаимодействия, а
– сила межфазного взаимодействия, а 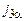 – производство энергии, обусловленное межкомпонентным взаимодействием.
– производство энергии, обусловленное межкомпонентным взаимодействием.  – вектор массовых сил, действующих на компонент
– вектор массовых сил, действующих на компонент  .
. ,
, ,
, ,
, ,
, ,
,
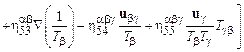 , (16.2)
, (16.2)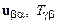 будем называть просто диффузионными скоростями и температурами. Конечно, в общем случае диффузионные скорости и температуры могут быть одного порядка величинами со скоростями и температурами компонентов смеси. Тогда соотношения (16.2) уже не применимы, однако методы термодинамики необратимых процессов и неравновесная статистической механики и в этом случае позволяют построить определяющие соотношения.
будем называть просто диффузионными скоростями и температурами. Конечно, в общем случае диффузионные скорости и температуры могут быть одного порядка величинами со скоростями и температурами компонентов смеси. Тогда соотношения (16.2) уже не применимы, однако методы термодинамики необратимых процессов и неравновесная статистической механики и в этом случае позволяют построить определяющие соотношения.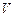 , ограниченный поверхностью
, ограниченный поверхностью  . Каждая из фаз занимает объем
. Каждая из фаз занимает объем  ,
,  – объем, занятый несущей средой, а
– объем, занятый несущей средой, а 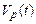 – объем, занятый дисперсной фазой, а
– объем, занятый дисперсной фазой, а  . Соответственно часть граничной поверхности
. Соответственно часть граничной поверхности 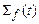 проходит через первую фазу, а
проходит через первую фазу, а 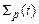 – через вторую,
– через вторую,  . Обычно считается, что несущая среда является топологически связной, а дисперсная нет. Таким образом, в объеме
. Обычно считается, что несущая среда является топологически связной, а дисперсная нет. Таким образом, в объеме 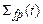 . Предполагается, что внутри объема, занимаемого фазой
. Предполагается, что внутри объема, занимаемого фазой 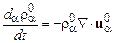 ,
,  ,
,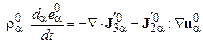 ,
,  , (16.3)
, (16.3)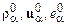 – плотность, скорость и внутренняя энергия компонента
– плотность, скорость и внутренняя энергия компонента 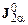 ,
,  – соответствующие значения тензора напряжений и вектора потока тепла. Система уравнений (16.3) замыкается уравнениями состояния фаз и их определяющими соотношениями. Обычно предполагается, что фазы представляют собой ньютоновские жидкости, т. е.
– соответствующие значения тензора напряжений и вектора потока тепла. Система уравнений (16.3) замыкается уравнениями состояния фаз и их определяющими соотношениями. Обычно предполагается, что фазы представляют собой ньютоновские жидкости, т. е.
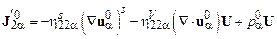 ,
,
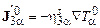 ,
, 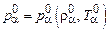 . (16.4)
. (16.4)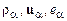 , которые получаются из
, которые получаются из  . В результате осреднения уравнений (16.3) получаются уравнения для переменных
. В результате осреднения уравнений (16.3) получаются уравнения для переменных 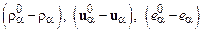 .
.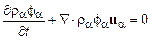 ,
, , (16.5)
, (16.5)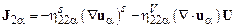 ,
,
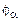 . Их появление связано с усреднением уравнений. Кроме того, в этих уравнениях фигурируют общее давление и, вообще говоря, общий тензор напряжений. В этом смысле можно говорить, что в результате усреднения мы получаем уравнения некоторой квазиоднородной среды с общим давлением и напряжениями.
. Их появление связано с усреднением уравнений. Кроме того, в этих уравнениях фигурируют общее давление и, вообще говоря, общий тензор напряжений. В этом смысле можно говорить, что в результате усреднения мы получаем уравнения некоторой квазиоднородной среды с общим давлением и напряжениями. . (17.1)
. (17.1) , (17.2)
, (17.2)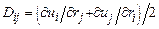 .
.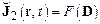 . (17.3)
. (17.3)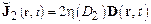 . (17.4)
. (17.4) – второй инвариант тензора скоростей деформации[46].
– второй инвариант тензора скоростей деформации[46].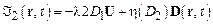 . (17.5)
. (17.5)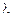 – положительная константа, а
– положительная константа, а 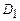 – первый инвариант тензора скоростей деформации. Роль давления здесь играет комплекс
– первый инвариант тензора скоростей деформации. Роль давления здесь играет комплекс 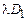 .
. со скоростью
со скоростью 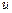 , а пластины перпендикулярны оси
, а пластины перпендикулярны оси 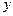 . Для ньютоновских жидкостей течение это характеризуется линейным профилем скорости
. Для ньютоновских жидкостей течение это характеризуется линейным профилем скорости 

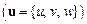 , где параметр
, где параметр 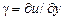 задает величину скорости сдвига. Тензор напряжений имеет в этом случае две ненулевые составляющие
задает величину скорости сдвига. Тензор напряжений имеет в этом случае две ненулевые составляющие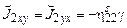 . (17.6)
. (17.6)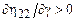 , (17.7)
, (17.7) . (17.8)
. (17.8) , разделяют их.
, разделяют их.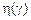 называют кажущейся вязкостью. Эта вязкость, однако, вполне наблюдаемая и определяется отношением
называют кажущейся вязкостью. Эта вязкость, однако, вполне наблюдаемая и определяется отношением 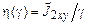 . Так, например, эксперименты показывают, что для псевдопластических жидкостей кажущаяся вязкость с увеличением скорости сдвига остается постоянной, затем уменьшается, а потом выходит на асимптоту (рис. 17.1).
. Так, например, эксперименты показывают, что для псевдопластических жидкостей кажущаяся вязкость с увеличением скорости сдвига остается постоянной, затем уменьшается, а потом выходит на асимптоту (рис. 17.1). , (17.9)
, (17.9)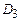 – третий инвариант тензора скоростей деформации, а функцию
– третий инвариант тензора скоростей деформации, а функцию  называют поперечной вязкостью.
называют поперечной вязкостью.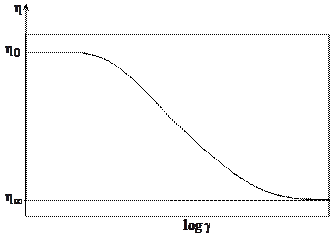
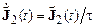 ,
, – некоторое время релаксации. Это уравнение описывает релаксацию напряжения от заданного начального значения
– некоторое время релаксации. Это уравнение описывает релаксацию напряжения от заданного начального значения 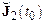 до нуля[47]. Однако, например, в ньютоновских жидкостях напряжения должны приобретать вид (12.16), и мы приходим к уравнению Максвелла[48]
до нуля[47]. Однако, например, в ньютоновских жидкостях напряжения должны приобретать вид (12.16), и мы приходим к уравнению Максвелла[48]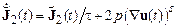 . (17.10)
. (17.10)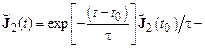
 (17.11)
(17.11)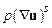 не изменяется заметным образом на временах
не изменяется заметным образом на временах  , то соотношение (17.11) сводится к такому:
, то соотношение (17.11) сводится к такому: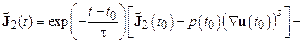
 . (17.12)
. (17.12) мы имеем обычные ньютоновские определяющие соотношения.
мы имеем обычные ньютоновские определяющие соотношения.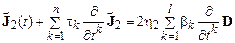 . (17.13)
. (17.13)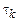 – набор времен релаксации, а
– набор времен релаксации, а  – некоторые посто-янные.
– некоторые посто-янные.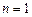 . Недостатки подобных моделей очевидны, эти модели содержат большое число параметров, часть из которых просто ненаблюдаемые. Кроме того, они включают временные производные от тензоров напряжений и скоростей деформаций высших порядков, а это, вообще говоря, требует учета всех нелинейных членов в тензоре напряжений. Подобные нелинейные определяющие соотношения будут обсуждаться в следующем разделе.
. Недостатки подобных моделей очевидны, эти модели содержат большое число параметров, часть из которых просто ненаблюдаемые. Кроме того, они включают временные производные от тензоров напряжений и скоростей деформаций высших порядков, а это, вообще говоря, требует учета всех нелинейных членов в тензоре напряжений. Подобные нелинейные определяющие соотношения будут обсуждаться в следующем разделе. (17.14)
(17.14)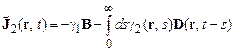 . (17.15)
. (17.15)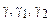 – некоторые постоянные (
– некоторые постоянные (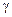 – модуль сдвига), а
– модуль сдвига), а  – тензор деформаций.
– тензор деформаций.


