Рассмотрим функцию, дифференцируемую на некотором промежутке. Функцию  называют выпуклой вниз (вверх) на этом промежутке, если ее график расположен не ниже (не выше) касательной, проведенной в произвольной точке этого промежутка. Соответственно график называют выпуклым вниз (вверх) на этом промежутке.
называют выпуклой вниз (вверх) на этом промежутке, если ее график расположен не ниже (не выше) касательной, проведенной в произвольной точке этого промежутка. Соответственно график называют выпуклым вниз (вверх) на этом промежутке.
На рис. 3.16 приведен график функции  , выпуклой вниз на промежутках
, выпуклой вниз на промежутках  и
и  выпуклой вверх на промежутках
выпуклой вверх на промежутках 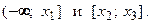
Согласно определению, о направлении выпуклости судят по расположению графика относительно касательной. На рис. 3.16 нанесены касательные, проведенные в точках с абсциссами  меньшими
меньшими  Как видно, график функции лежит под обеими касательными и на промежутке
Как видно, график функции лежит под обеими касательными и на промежутке 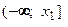 является выпуклым вверх. Аналогичным способом можно обосновать наличие остальных промежутков выпуклости вверх или вниз.
является выпуклым вверх. Аналогичным способом можно обосновать наличие остальных промежутков выпуклости вверх или вниз.
Точкой перегиба функции  называют точку
называют точку 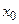 , принадлежащую области определения, при переходе через которую меняется направление выпуклости функции. Соответствующую точку
, принадлежащую области определения, при переходе через которую меняется направление выпуклости функции. Соответствующую точку 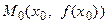 графика функции называют точкой перегиба графика функции. В точке перегиба графика изменяется направление выпуклости: при переходе подвижной точки вдоль кривой, описываемой функцией, график из выпуклого вниз становится выпуклым вверх, и наоборот. Говорят, что в точке перегиба график переходит с одной стороной касательной на другую.
графика функции называют точкой перегиба графика функции. В точке перегиба графика изменяется направление выпуклости: при переходе подвижной точки вдоль кривой, описываемой функцией, график из выпуклого вниз становится выпуклым вверх, и наоборот. Говорят, что в точке перегиба график переходит с одной стороной касательной на другую.
Для функции  , приведенной на рис. 3.16, точки
, приведенной на рис. 3.16, точки  являются точками перегиба функции, так как при переходе через эти точки меняется направление выпуклости. При переходе через точку
являются точками перегиба функции, так как при переходе через эти точки меняется направление выпуклости. При переходе через точку 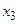 также меняется направление выпуклости, но эта точка не принадлежит области определения, и поэтому не является точкой перегиба.
также меняется направление выпуклости, но эта точка не принадлежит области определения, и поэтому не является точкой перегиба.
Чтобы найти промежутки выпуклости и точки перегиба, используют теоремы, приведенные ниже.
Теорема 3.19 (достаточное условие выпуклости функции на промежутке). Если вторая производная функции положительна (отрицательна) на некотором промежутке, то функция выпукла вниз (вверх) на этом промежутке.
В частности, если  в каждой точке некоторого интервала
в каждой точке некоторого интервала 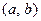 , то
, то  выпукла вниз на этом интервале. Если
выпукла вниз на этом интервале. Если 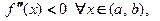 то
то  выпукла вверх на этом интервале.
выпукла вверх на этом интервале.
Сформулированное правило можно назвать правилом «улыбки», ассоциируя знак «+» второй производной с хорошим настроением и улыбкой ( ), а знак «−» с плохим настроением и грустной гримасой (
), а знак «−» с плохим настроением и грустной гримасой (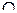 ).
).
Теорема 3.20 (необходимое условие перегиба). Если 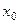 − точка перегиба функции
− точка перегиба функции  , то вторая производная
, то вторая производная  в точке перегиба равна нулю или конечная вторая производная не существует:
в точке перегиба равна нулю или конечная вторая производная не существует:
 (3.37)
(3.37)
Точки, принадлежащие области определения функции 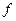 и удовлетворяющие совокупности (3.37), называют критическими точками второго рода функции
и удовлетворяющие совокупности (3.37), называют критическими точками второго рода функции 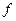 (критическими точками функции по второй производной). В этих точках возможен перегиб графика. Среди критических точек 2-го рода нужно делать отбор при помощи достаточных условий перегиба.
(критическими точками функции по второй производной). В этих точках возможен перегиб графика. Среди критических точек 2-го рода нужно делать отбор при помощи достаточных условий перегиба.
Теорема 3.21 (достаточное условие перегиба). Если вторая производная меняет знак при переходе через критическую точку 2-го рода функции 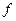 , то эта точка является точкой перегиба функции.
, то эта точка является точкой перегиба функции.
Заметим, что есть еще одно правило выделения точек перегиба из множества критических точек 2-го рода. Оно сформулировано в теореме 3.18. Из этой теоремы следует, что если стационарная точка функции не является точкой экстремума, то эта точка есть точка перегиба.
Алгоритм исследования функции на выпуклость
и точки перегиба
1. Найти область определения функции  .
.
2. Найти вторую производную  .
.
3. Найти критические точки 2-го рода из условий  и
и 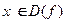 .
.
4. Исследовать знак второй производной 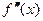 по обе стороны от каждой критической точки и сделать вывод о промежутках выпуклости и точках перегиба.
по обе стороны от каждой критической точки и сделать вывод о промежутках выпуклости и точках перегиба.
5. Найти значения функции в точках перегиба и точки перегиба графика.
Ниже приведены примеры, в которых продолжены исследования функций, рассмотренных в примерах (3.35)−(3.39).
Пример 3.40. Найти промежутки выпуклости и точки перегиба функции 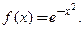
□ 1. Область определения 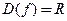 .
.
2. Найдем вторую производную:

3. Найдем критические точки 2-го рода:
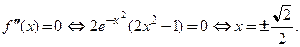
4. Исследуем знак второй производной. Так как  при
при  , то функция выпукла вниз на этих промежутках. Так как
, то функция выпукла вниз на этих промежутках. Так как  при
при  , то функция выпукла вверх на этом отрезке. При переходе через точки
, то функция выпукла вверх на этом отрезке. При переходе через точки 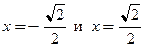 вторая производная меняет знак. Поэтому эти точки являются точками перегиба функции.
вторая производная меняет знак. Поэтому эти точки являются точками перегиба функции.
 На рис. 3.16 указываем направления выпуклости графика. Обе критические точки являются точками перегиба, так как они разделяют интервалы, в которых функция выпукла вниз и вверх.
На рис. 3.16 указываем направления выпуклости графика. Обе критические точки являются точками перегиба, так как они разделяют интервалы, в которых функция выпукла вниз и вверх.
5. Вычисляем значения функции в точках перегиба: 
 Точки перегиба графика:
Точки перегиба графика: 
 ■
■
Пример 3.41. Найти промежутки выпуклости и точки перегиба функции 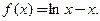
□ 1. Область определения  .
.
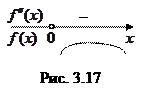 2. Найдем вторую производную:
2. Найдем вторую производную: 
3. В области определения критических точек
2-го рода нет, так как при  .
.
4. Знак второй производной отрицательный во всей области определения. Следовательно, функция выпукла вверх во всей области определения  . Точек перегиба нет.
. Точек перегиба нет.
5. − ■
 Пример 3.42. Найти промежутки выпуклости и точки перегиба функции
Пример 3.42. Найти промежутки выпуклости и точки перегиба функции 
□ 1. 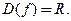 2.
2. 
3. 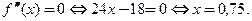
4. Определим знаки второй производной:
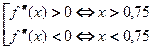 (см. рис.3.18).
(см. рис.3.18).
Функция 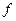 выпукла вниз при
выпукла вниз при 
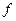 выпукла вверх при
выпукла вверх при  Точка
Точка  − точка перегиба функции.
− точка перегиба функции.
5.  Точка перегиба графика имеет координаты
Точка перегиба графика имеет координаты 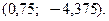 ■
■
Пример 3.43. Найти промежутки выпуклости и точки перегиба функции 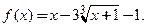
□ 1. Область определения 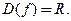
2. Найдем вторую производную: 
3. Критическая точка 2-го рода находится из условия:  Отсюда
Отсюда  − критическая точка 2-го рода.
− критическая точка 2-го рода.
 4. Исследуем знаки второй производной
4. Исследуем знаки второй производной  и получим:
и получим:  Следовательно, функция
Следовательно, функция 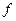 выпукла вниз на промежутке
выпукла вниз на промежутке  и выпукла вверх на промежутке
и выпукла вверх на промежутке  Точка
Точка 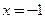 является точкой перегиба.
является точкой перегиба.
5. 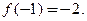 Точка перегиба графика имеет координаты
Точка перегиба графика имеет координаты  ■
■
Асимптоты графика функции
Асимптотой графика функции 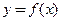 называют такую линию на плоскости, что расстояние от точки
называют такую линию на плоскости, что расстояние от точки  до этой линии стремится к нулю при неограниченном удалении точки графика от начала координат.
до этой линии стремится к нулю при неограниченном удалении точки графика от начала координат.
Ограничимся рассмотрением прямых линий в качестве асимптот. График функции 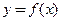 может иметь вертикальные, горизонтальные и наклонные асимптоты.
может иметь вертикальные, горизонтальные и наклонные асимптоты.
Вертикальная прямая  называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 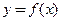 , если хотя бы один односторонний предел при
, если хотя бы один односторонний предел при 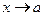 равен бесконечности:
равен бесконечности:  или
или 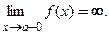
Существование вертикальной асимптоты  графика функции
графика функции 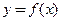 означает, что при
означает, что при  (или при
(или при  ) функция стремится к бесконечности монотонно, если в соответствующей односторонней окрестности точки
) функция стремится к бесконечности монотонно, если в соответствующей односторонней окрестности точки  производная функции не меняет знак. Говорят, что график функции неограниченно приближается к вертикальной прямой
производная функции не меняет знак. Говорят, что график функции неограниченно приближается к вертикальной прямой  ...................................
...................................
Вертикальные асимптоты проходят через точки разрыва второго рода или граничные точки области определения, в которых хотя бы односторонний предел при 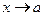 равен бесконечности.
равен бесконечности.
Если функция 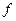 определена для всех
определена для всех  и существует конечный предел
и существует конечный предел 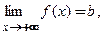 то горизонтальная прямая
то горизонтальная прямая 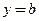 называется горизонтальной асимптотой при
называется горизонтальной асимптотой при 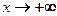 , или правосторонней (правой) горизонтальной асимптотой. Аналогично определяется горизонтальная асимптота при
, или правосторонней (правой) горизонтальной асимптотой. Аналогично определяется горизонтальная асимптота при  . Существование горизонтальной асимптоты означает, что при
. Существование горизонтальной асимптоты означает, что при 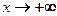 (или при
(или при  ) функция
) функция 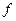 ведет себя «почти как» постоянная
ведет себя «почти как» постоянная 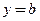 с точностью до бесконечно малой.
с точностью до бесконечно малой.
Если функция 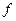 определена для всех
определена для всех  и представима в виде
и представима в виде  при
при 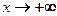 , где слагаемое
, где слагаемое  является бесконечно малой величиной высшего порядка малости относительно
является бесконечно малой величиной высшего порядка малости относительно  , то наклонная прямая
, то наклонная прямая  называется наклонной асимптотой при
называется наклонной асимптотой при 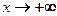 , или правосторонней (правой) наклонной асимптотой. Аналогично определяют наклонную асимптоту при
, или правосторонней (правой) наклонной асимптотой. Аналогично определяют наклонную асимптоту при  . Если существует наклонная асимптота при
. Если существует наклонная асимптота при 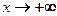 (или при
(или при  ), то график функции при
), то график функции при 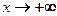 (или при
(или при  ) ведет себя «почти как» наклонная прямая
) ведет себя «почти как» наклонная прямая  с точностью до бесконечно малой.
с точностью до бесконечно малой.
Теорема 3.22. Пусть функция 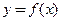 определена для всех
определена для всех  . Чтобы прямая
. Чтобы прямая  была наклонной асимптотой графика функции при
была наклонной асимптотой графика функции при  необходимо и достаточно, чтобы существовали конечные пределы:
необходимо и достаточно, чтобы существовали конечные пределы:  и
и 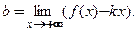
Аналогично находят наклонную асимптоту при 
Пример 3.44. Найти асимптоты графика функции 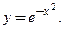
□ Функция 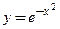 определена и непрерывна на всей числовой оси, следовательно, не имеет точек разрыва и поэтому у нее нет вертикальных асимптот.
определена и непрерывна на всей числовой оси, следовательно, не имеет точек разрыва и поэтому у нее нет вертикальных асимптот.
 Найдем предел:
Найдем предел:
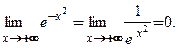
Отсюда следует, что 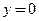 является правой горизонтальной асимптотой заданной кривой. С учетом четности функции
является правой горизонтальной асимптотой заданной кривой. С учетом четности функции  ясно, что ось абсцисс является одновременно и левосторонней, и правосторонней горизонтальной асимптотой. При больших по абсолютной величине значениях
ясно, что ось абсцисс является одновременно и левосторонней, и правосторонней горизонтальной асимптотой. При больших по абсолютной величине значениях  график функции слабо отклоняется от оси абсцисс (см. рис.3.20). ■
график функции слабо отклоняется от оси абсцисс (см. рис.3.20). ■
Пример 3.45. Найти асимптоты графика функции 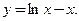
 □ Функция
□ Функция  определена и непрерывна при
определена и непрерывна при 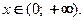
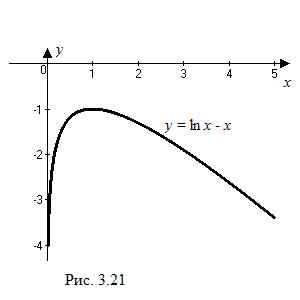
График функции имеет вертикальную асимптоту 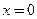 , проходящую через граничную точку области определения
, проходящую через граничную точку области определения 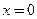 , так как
, так как  (см. рис. 3.21).
(см. рис. 3.21).
График не имеет правосторонней горизонтальной асимптоты, так как  (см. пример 3.32).
(см. пример 3.32).
Чтобы выяснить, имеет ли график правостороннюю наклонную асимптоту, вычислим пределы:

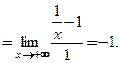
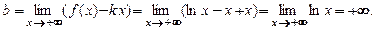 Второй предел не является конечным. Вывод: нет наклонной асимптоты.■
Второй предел не является конечным. Вывод: нет наклонной асимптоты.■
Пример 3.46. Найти асимптоты графика функции 
□ Функция 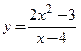 определена и непрерывна при
определена и непрерывна при 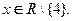 Точка
Точка  является точкой разрыва 2-го рода:
является точкой разрыва 2-го рода: 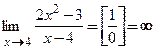 . Следовательно,
. Следовательно,  − вертикальная асимптота (см. рис. 3.22).
− вертикальная асимптота (см. рис. 3.22).
 График не имеет горизонтальных асимптот, так как
График не имеет горизонтальных асимптот, так как 

При вычислении предела использовано второе правило Лопиталя.
Наклонная асимптота 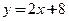 существует и является одновременно и левосторонней, и правосторонней асимптотой.
существует и является одновременно и левосторонней, и правосторонней асимптотой.
Действительно,

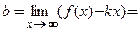
 ■
■



 называют выпуклой вниз (вверх) на этом промежутке, если ее график расположен не ниже (не выше) касательной, проведенной в произвольной точке этого промежутка. Соответственно график называют выпуклым вниз (вверх) на этом промежутке.
называют выпуклой вниз (вверх) на этом промежутке, если ее график расположен не ниже (не выше) касательной, проведенной в произвольной точке этого промежутка. Соответственно график называют выпуклым вниз (вверх) на этом промежутке. и
и  выпуклой вверх на промежутках
выпуклой вверх на промежутках 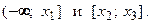
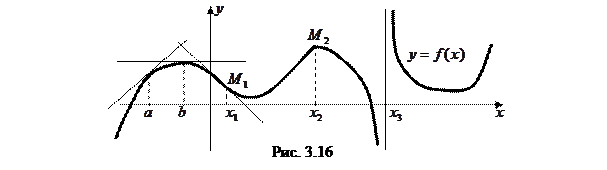
 меньшими
меньшими  Как видно, график функции лежит под обеими касательными и на промежутке
Как видно, график функции лежит под обеими касательными и на промежутке 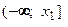 является выпуклым вверх. Аналогичным способом можно обосновать наличие остальных промежутков выпуклости вверх или вниз.
является выпуклым вверх. Аналогичным способом можно обосновать наличие остальных промежутков выпуклости вверх или вниз.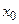 , принадлежащую области определения, при переходе через которую меняется направление выпуклости функции. Соответствующую точку
, принадлежащую области определения, при переходе через которую меняется направление выпуклости функции. Соответствующую точку 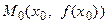 графика функции называют точкой перегиба графика функции. В точке перегиба графика изменяется направление выпуклости: при переходе подвижной точки вдоль кривой, описываемой функцией, график из выпуклого вниз становится выпуклым вверх, и наоборот. Говорят, что в точке перегиба график переходит с одной стороной касательной на другую.
графика функции называют точкой перегиба графика функции. В точке перегиба графика изменяется направление выпуклости: при переходе подвижной точки вдоль кривой, описываемой функцией, график из выпуклого вниз становится выпуклым вверх, и наоборот. Говорят, что в точке перегиба график переходит с одной стороной касательной на другую. являются точками перегиба функции, так как при переходе через эти точки меняется направление выпуклости. При переходе через точку
являются точками перегиба функции, так как при переходе через эти точки меняется направление выпуклости. При переходе через точку 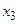 также меняется направление выпуклости, но эта точка не принадлежит области определения, и поэтому не является точкой перегиба.
также меняется направление выпуклости, но эта точка не принадлежит области определения, и поэтому не является точкой перегиба. в каждой точке некоторого интервала
в каждой точке некоторого интервала 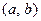 , то
, то 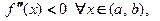 то
то  ), а знак «−» с плохим настроением и грустной гримасой (
), а знак «−» с плохим настроением и грустной гримасой ( ).
).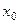 − точка перегиба функции
− точка перегиба функции  в точке перегиба равна нулю или конечная вторая производная не существует:
в точке перегиба равна нулю или конечная вторая производная не существует: (3.37)
(3.37)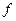 и удовлетворяющие совокупности (3.37), называют критическими точками второго рода функции
и удовлетворяющие совокупности (3.37), называют критическими точками второго рода функции  и
и 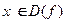 .
.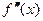 по обе стороны от каждой критической точки и сделать вывод о промежутках выпуклости и точках перегиба.
по обе стороны от каждой критической точки и сделать вывод о промежутках выпуклости и точках перегиба.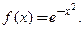
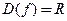 .
.
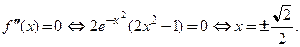
 при
при  , то функция выпукла вниз на этих промежутках. Так как
, то функция выпукла вниз на этих промежутках. Так как  при
при  , то функция выпукла вверх на этом отрезке. При переходе через точки
, то функция выпукла вверх на этом отрезке. При переходе через точки 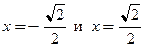 вторая производная меняет знак. Поэтому эти точки являются точками перегиба функции.
вторая производная меняет знак. Поэтому эти точки являются точками перегиба функции. На рис. 3.16 указываем направления выпуклости графика. Обе критические точки являются точками перегиба, так как они разделяют интервалы, в которых функция выпукла вниз и вверх.
На рис. 3.16 указываем направления выпуклости графика. Обе критические точки являются точками перегиба, так как они разделяют интервалы, в которых функция выпукла вниз и вверх. Точки перегиба графика:
Точки перегиба графика: 
 ■
■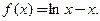
 .
.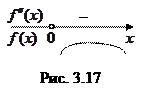 2. Найдем вторую производную:
2. Найдем вторую производную: 
 .
.  . Точек перегиба нет.
. Точек перегиба нет. Пример 3.42. Найти промежутки выпуклости и точки перегиба функции
Пример 3.42. Найти промежутки выпуклости и точки перегиба функции 
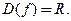 2.
2. 
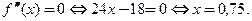
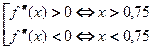 (см. рис.3.18).
(см. рис.3.18). 
 Точка
Точка  − точка перегиба функции.
− точка перегиба функции. Точка перегиба графика имеет координаты
Точка перегиба графика имеет координаты 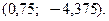 ■
■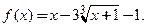

 Отсюда
Отсюда  − критическая точка 2-го рода.
− критическая точка 2-го рода. 4. Исследуем знаки второй производной
4. Исследуем знаки второй производной  Следовательно, функция
Следовательно, функция  и выпукла вверх на промежутке
и выпукла вверх на промежутке  Точка
Точка 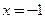 является точкой перегиба.
является точкой перегиба.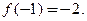 Точка перегиба графика имеет координаты
Точка перегиба графика имеет координаты  ■
■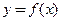 называют такую линию на плоскости, что расстояние от точки
называют такую линию на плоскости, что расстояние от точки  до этой линии стремится к нулю при неограниченном удалении точки графика от начала координат.
до этой линии стремится к нулю при неограниченном удалении точки графика от начала координат. называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 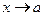 равен бесконечности:
равен бесконечности:  или
или 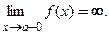
 (или при
(или при  ) функция стремится к бесконечности монотонно, если в соответствующей односторонней окрестности точки
) функция стремится к бесконечности монотонно, если в соответствующей односторонней окрестности точки  и существует конечный предел
и существует конечный предел 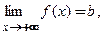 то горизонтальная прямая
то горизонтальная прямая 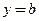 называется горизонтальной асимптотой при
называется горизонтальной асимптотой при 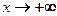 , или правосторонней (правой) горизонтальной асимптотой. Аналогично определяется горизонтальная асимптота при
, или правосторонней (правой) горизонтальной асимптотой. Аналогично определяется горизонтальная асимптота при  . Существование горизонтальной асимптоты означает, что при
. Существование горизонтальной асимптоты означает, что при 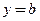 с точностью до бесконечно малой.
с точностью до бесконечно малой. при
при  является бесконечно малой величиной высшего порядка малости относительно
является бесконечно малой величиной высшего порядка малости относительно  , то наклонная прямая
, то наклонная прямая  называется наклонной асимптотой при
называется наклонной асимптотой при  необходимо и достаточно, чтобы существовали конечные пределы:
необходимо и достаточно, чтобы существовали конечные пределы:  и
и 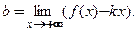

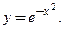
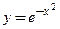 определена и непрерывна на всей числовой оси, следовательно, не имеет точек разрыва и поэтому у нее нет вертикальных асимптот.
определена и непрерывна на всей числовой оси, следовательно, не имеет точек разрыва и поэтому у нее нет вертикальных асимптот. Найдем предел:
Найдем предел: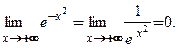
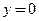 является правой горизонтальной асимптотой заданной кривой. С учетом четности функции
является правой горизонтальной асимптотой заданной кривой. С учетом четности функции  ясно, что ось абсцисс является одновременно и левосторонней, и правосторонней горизонтальной асимптотой. При больших по абсолютной величине значениях
ясно, что ось абсцисс является одновременно и левосторонней, и правосторонней горизонтальной асимптотой. При больших по абсолютной величине значениях 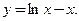
 □ Функция
□ Функция  определена и непрерывна при
определена и непрерывна при 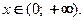
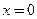 , проходящую через граничную точку области определения
, проходящую через граничную точку области определения  (см. рис. 3.21).
(см. рис. 3.21). (см. пример 3.32).
(см. пример 3.32).
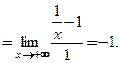
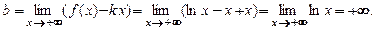 Второй предел не является конечным. Вывод: нет наклонной асимптоты.■
Второй предел не является конечным. Вывод: нет наклонной асимптоты.■
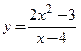 определена и непрерывна при
определена и непрерывна при 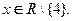 Точка
Точка  является точкой разрыва 2-го рода:
является точкой разрыва 2-го рода: 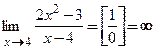 . Следовательно,
. Следовательно,  График не имеет горизонтальных асимптот, так как
График не имеет горизонтальных асимптот, так как 

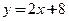 существует и является одновременно и левосторонней, и правосторонней асимптотой.
существует и является одновременно и левосторонней, и правосторонней асимптотой.
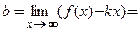
 ■
■


