Теорема 3.4 (о дифференцированиисуммы, разности, произведения и частного функций). Пусть функции  определены в некоторой окрестности точки
определены в некоторой окрестности точки 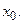 Если эти функции дифференцируемы в точке
Если эти функции дифференцируемы в точке 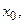 то их сумма, разность, произведение и частное также дифференцируемы в точке
то их сумма, разность, произведение и частное также дифференцируемы в точке 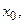 при этом в точке
при этом в точке 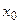 имеют место соотношения, приведенные в табл. 3.2.
имеют место соотношения, приведенные в табл. 3.2.
Таблица 3.2
| Производные
| Дифференциалы
|
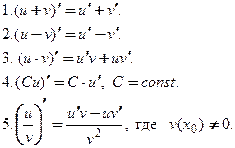
|

|
Эти формулы называют общими правилами дифференцирования.
Если точка  не указана, то функцию дифференцируют при произвольном значении
не указана, то функцию дифференцируют при произвольном значении  , принадлежащем области определения функции. Если точка
, принадлежащем области определения функции. Если точка 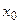 указана, то сначала функцию дифференцируют при произвольном значении
указана, то сначала функцию дифференцируют при произвольном значении  , принадлежащем области определения функции, а затем вычисляют значение производной или дифференциала в точке
, принадлежащем области определения функции, а затем вычисляют значение производной или дифференциала в точке 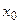 .
.
Пример 3.7. Найти производную функции 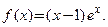
□ Применим правило 3 дифференцирования произведения функций:  . Затем по правилу 2 из табл. 3.2 находим производную разности двух функций:
. Затем по правилу 2 из табл. 3.2 находим производную разности двух функций:  Производные
Производные 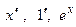 взяты из табл. 3.1 (см. формулы 2, 1 и 3 соответственно):
взяты из табл. 3.1 (см. формулы 2, 1 и 3 соответственно): 

 Подставим эти производные и получим:
Подставим эти производные и получим: 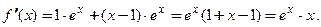 ■
■
Пример 3.8. Найти производную и дифференциал функции 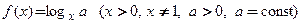 в точке
в точке 
□ Преобразуем логарифмическую функцию, произведя переход к основанию, равному числу 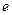 , по формуле:
, по формуле: 
Найдем производную и дифференциал в произвольной точке 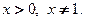 Для этого воспользуемся правилом 5 дифференцирования частного и формулами 1 и 4 из табл. 3.1 для производных функций
Для этого воспользуемся правилом 5 дифференцирования частного и формулами 1 и 4 из табл. 3.1 для производных функций  соответственно:
соответственно:
 . Дифференциал выразим по формуле (3.5):
. Дифференциал выразим по формуле (3.5):
 .
.
Теперь в найденные выражения подставим  и получим:
и получим:  ■
■
3.2.3.Дифференцирование сложной и неявной функции. Инвариантное свойство дифференциала
Теорема 3.5 (о производной сложной функции). Если функция  дифференцируема в точке
дифференцируема в точке  , функция
, функция  дифференцируема в точке
дифференцируема в точке  то сложная функция
то сложная функция  дифференцируема в точке
дифференцируема в точке 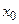 и ее производная в этой точке вычисляется по формуле:
и ее производная в этой точке вычисляется по формуле:
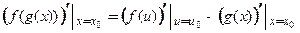 , или кратко
, или кратко  (3.7)
(3.7)
В точке 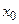 верна и такая запись:
верна и такая запись:  . Переменные
. Переменные  называют зависимой и независимой переменной дифференцирования соответственно.
называют зависимой и независимой переменной дифференцирования соответственно.
Правило дифференцирования сложной функции приводит к важному свойству, называемому инвариантным свойством первого дифференциала.
Дифференциал функции  записывается в одной и той же форме
записывается в одной и той же форме
 , (3.8)
, (3.8)
как в случае независимой, так и в случае зависимой переменной  .
.
Из этого свойства следует, что формула для вычисления дифференциала 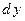 единая, не зависящая от вида переменной
единая, не зависящая от вида переменной  Различие состоит лишь в способе вычисления дифференциала
Различие состоит лишь в способе вычисления дифференциала 
1) для независимой переменной  дифференциал
дифференциал 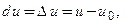
2) для зависимой переменной 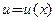 дифференциал вычисляется по формуле
дифференциал вычисляется по формуле 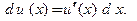
Пример 3.9. Найти производную и дифференциал сложной функции 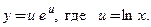
□ По формуле (3.7) имеем:

Далее пользуемся формулой (3.5): 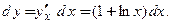
Заметим, этот результат можно было получить другим способом − методом исключения зависимой переменной 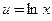 :
: 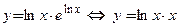 , и последующим дифференцированием полученного произведения:
, и последующим дифференцированием полученного произведения:  ■
■
Пример 3.10. Найти производную и дифференциал функции 
□ Запишем эту сложную функцию  в виде композиции двух функций:
в виде композиции двух функций:  Применим формулу (3.7) и получим:
Применим формулу (3.7) и получим: 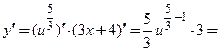
 Подставим производную в формулу (3.5) и найдем дифференциал:
Подставим производную в формулу (3.5) и найдем дифференциал: 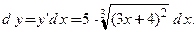
При  значение производной равно
значение производной равно  Выражение для дифференциала имеет вид
Выражение для дифференциала имеет вид  и является линейной функцией дифференциала
и является линейной функцией дифференциала  ■
■
Дифференцирование неявной функции с помощью правила дифференцирования сложной функции
Правило дифференцирования сложной функции можно применять при нахождении производных и дифференциалов неявных фунций.
Рассмотрим уравнение 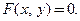 Это соотношение называют неявным уравнением, связывающим неявную функцию
Это соотношение называют неявным уравнением, связывающим неявную функцию  и независимую переменную
и независимую переменную  (см. раздел 1.3.2).
(см. раздел 1.3.2).
Например, уравнения  и
и  определяют одну и ту же функцию, но отличаются друг от друга формой представления. В первом случае квадратичная функция задана явно, а во втором − неявно.
определяют одну и ту же функцию, но отличаются друг от друга формой представления. В первом случае квадратичная функция задана явно, а во втором − неявно.
Будем полагать, что на множестве D существует дифференцируемая функция 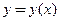 , обращающая уравнение в тождество
, обращающая уравнение в тождество 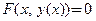 . Дифференцируя обе его части как сложную функцию по переменной
. Дифференцируя обе его части как сложную функцию по переменной  , получим линейное уравнение относительно производной
, получим линейное уравнение относительно производной 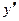 . Решив его, найдем производную
. Решив его, найдем производную 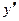 в виде функции переменных
в виде функции переменных 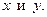 Тогда по формуле (3.5) дифференциал
Тогда по формуле (3.5) дифференциал 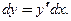
Покажем, что выражения для производной функции, заданной соотношениями  и
и  , совпадают. В первом случае (явное задание функции):
, совпадают. В первом случае (явное задание функции): 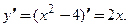 Во втором (неявное задание функции):
Во втором (неявное задание функции): 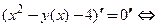
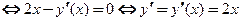 . Как видим, результат не зависит от способа его получения.
. Как видим, результат не зависит от способа его получения.
Если в качестве независимой переменной выбрана переменная  , то уравнение
, то уравнение  можно рассматривать как соотношение, определяющее неявную функцию
можно рассматривать как соотношение, определяющее неявную функцию  Поиск производной
Поиск производной  (
(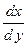 ) и дифференциала
) и дифференциала  выполняют способом, аналогичным выше описанному.
выполняют способом, аналогичным выше описанному.
Пример 3.11. Найти производную 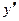 и дифференциал
и дифференциал 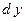 функции, заданной неявно уравнением
функции, заданной неявно уравнением 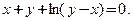
□ Полагаем, что существует функция 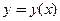 независимой переменной
независимой переменной  , удовлетворяющая заданному уравнению. Дифференцируем данное соотношение по
, удовлетворяющая заданному уравнению. Дифференцируем данное соотношение по 

Уединим производную и получим:  .
.
По формуле (3.5) 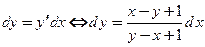 . ■
. ■
Другой способ отыскания производной неявной функции с формулировкой условий ее существования рассмотрен в разделе 5.2.9.



 определены в некоторой окрестности точки
определены в некоторой окрестности точки 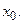 Если эти функции дифференцируемы в точке
Если эти функции дифференцируемы в точке 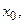 то их сумма, разность, произведение и частное также дифференцируемы в точке
то их сумма, разность, произведение и частное также дифференцируемы в точке 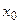 имеют место соотношения, приведенные в табл. 3.2.
имеют место соотношения, приведенные в табл. 3.2.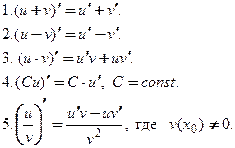

 не указана, то функцию дифференцируют при произвольном значении
не указана, то функцию дифференцируют при произвольном значении  , принадлежащем области определения функции. Если точка
, принадлежащем области определения функции. Если точка 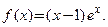
 . Затем по правилу 2 из табл. 3.2 находим производную разности двух функций:
. Затем по правилу 2 из табл. 3.2 находим производную разности двух функций:  Производные
Производные 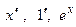 взяты из табл. 3.1 (см. формулы 2, 1 и 3 соответственно):
взяты из табл. 3.1 (см. формулы 2, 1 и 3 соответственно): 

 Подставим эти производные и получим:
Подставим эти производные и получим: 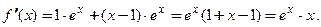 ■
■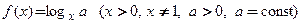 в точке
в точке 
 , по формуле:
, по формуле: 
 Для этого воспользуемся правилом 5 дифференцирования частного и формулами 1 и 4 из табл. 3.1 для производных функций
Для этого воспользуемся правилом 5 дифференцирования частного и формулами 1 и 4 из табл. 3.1 для производных функций  соответственно:
соответственно: . Дифференциал выразим по формуле (3.5):
. Дифференциал выразим по формуле (3.5): .
. и получим:
и получим:  ■
■ дифференцируема в точке
дифференцируема в точке  , функция
, функция  дифференцируема в точке
дифференцируема в точке  то сложная функция
то сложная функция  дифференцируема в точке
дифференцируема в точке 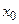 и ее производная в этой точке вычисляется по формуле:
и ее производная в этой точке вычисляется по формуле: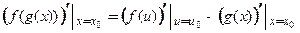 , или кратко
, или кратко  (3.7)
(3.7) . Переменные
. Переменные  называют зависимой и независимой переменной дифференцирования соответственно.
называют зависимой и независимой переменной дифференцирования соответственно. , (3.8)
, (3.8) .
.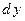 единая, не зависящая от вида переменной
единая, не зависящая от вида переменной  Различие состоит лишь в способе вычисления дифференциала
Различие состоит лишь в способе вычисления дифференциала 
 дифференциал
дифференциал 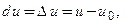
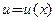 дифференциал вычисляется по формуле
дифференциал вычисляется по формуле 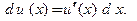
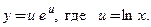

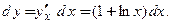
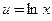 :
: 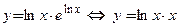 , и последующим дифференцированием полученного произведения:
, и последующим дифференцированием полученного произведения:  ■
■
 в виде композиции двух функций:
в виде композиции двух функций:  Применим формулу (3.7) и получим:
Применим формулу (3.7) и получим: 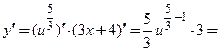
 Подставим производную в формулу (3.5) и найдем дифференциал:
Подставим производную в формулу (3.5) и найдем дифференциал: 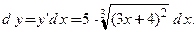
 значение производной равно
значение производной равно  Выражение для дифференциала имеет вид
Выражение для дифференциала имеет вид  и является линейной функцией дифференциала
и является линейной функцией дифференциала  ■
■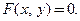 Это соотношение называют неявным уравнением, связывающим неявную функцию
Это соотношение называют неявным уравнением, связывающим неявную функцию  и независимую переменную
и независимую переменную  (см. раздел 1.3.2).
(см. раздел 1.3.2). и
и  определяют одну и ту же функцию, но отличаются друг от друга формой представления. В первом случае квадратичная функция задана явно, а во втором − неявно.
определяют одну и ту же функцию, но отличаются друг от друга формой представления. В первом случае квадратичная функция задана явно, а во втором − неявно.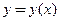 , обращающая уравнение в тождество
, обращающая уравнение в тождество 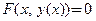 . Дифференцируя обе его части как сложную функцию по переменной
. Дифференцируя обе его части как сложную функцию по переменной 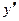 . Решив его, найдем производную
. Решив его, найдем производную 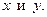 Тогда по формуле (3.5) дифференциал
Тогда по формуле (3.5) дифференциал 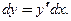
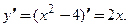 Во втором (неявное задание функции):
Во втором (неявное задание функции): 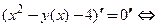
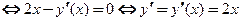 . Как видим, результат не зависит от способа его получения.
. Как видим, результат не зависит от способа его получения. , то уравнение
, то уравнение  можно рассматривать как соотношение, определяющее неявную функцию
можно рассматривать как соотношение, определяющее неявную функцию  Поиск производной
Поиск производной  (
(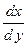 ) и дифференциала
) и дифференциала  выполняют способом, аналогичным выше описанному.
выполняют способом, аналогичным выше описанному.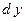 функции, заданной неявно уравнением
функции, заданной неявно уравнением 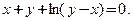
 независимой переменной
независимой переменной 

 .
.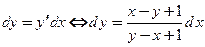 . ■
. ■

