производные высших порядков
Рассмотрим функцию  , заданную явно и имеющую конечную производную
, заданную явно и имеющую конечную производную  в любой точке
в любой точке  промежутка
промежутка 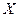 . Если функция
. Если функция  имеет производную (конечную или бесконечную) в каждой точке
имеет производную (конечную или бесконечную) в каждой точке 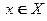 , то эту производную называют производной 2-го порядка (второй производной) функции
, то эту производную называют производной 2-го порядка (второй производной) функции  и обозначают
и обозначают 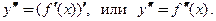
Если в свою очередь функция 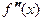 имеет производную
имеет производную 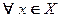 , то ее производная называется производной 3-го порядка (третьей производной):
, то ее производная называется производной 3-го порядка (третьей производной): 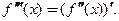 Аналогично берутся производные более высоких порядков.
Аналогично берутся производные более высоких порядков.
Если в каждой точке промежутка 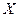 существует конечная производная (п− 1)-го порядка
существует конечная производная (п− 1)-го порядка 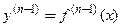 , то производная n-го порядка по определению равна производной от производной
, то производная n-го порядка по определению равна производной от производной  -го порядка:
-го порядка:
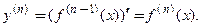 (3.13)
(3.13)
Порядок производной − число п − определяет число операций дифференцирования, которому подвергается функция. Поэтому естественно за производную нулевого порядка принять саму функцию:  . Таким образом, допустимы следующие значения числа п: 0; 1; 2;…; k;… Производные, порядки которых больше единицы (
. Таким образом, допустимы следующие значения числа п: 0; 1; 2;…; k;… Производные, порядки которых больше единицы ( ), называют производными высших порядков.
), называют производными высших порядков.
Для производной n -го порядка в произвольной точке  используют следующие обозначения:
используют следующие обозначения: 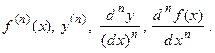 Круглые скобки в знаменателе обычно не пишут. Если порядок производной − конкретное число, то его обозначают штрихами (для производных до третьего порядка включительно), а также записывают римской цифрой без скобок или арабской в скобках:
Круглые скобки в знаменателе обычно не пишут. Если порядок производной − конкретное число, то его обозначают штрихами (для производных до третьего порядка включительно), а также записывают римской цифрой без скобок или арабской в скобках:

Если производная п -го порядка функции  в точке
в точке 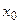 существует, то ее значение − число (собственное (конечное) или несобственное
существует, то ее значение − число (собственное (конечное) или несобственное 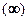 ), которое обозначается одним из следующих способов:
), которое обозначается одним из следующих способов: 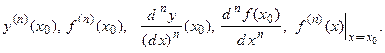
Если производная п-го порядка конечна в точке 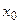 , то в некоторой ее окрестности определены и непрерывны и сама функция
, то в некоторой ее окрестности определены и непрерывны и сама функция  , и все ее производные до
, и все ее производные до 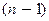 -го порядка включительно. Это утверждение можно доказать, опираясь на теорему 3.2.
-го порядка включительно. Это утверждение можно доказать, опираясь на теорему 3.2.
В граничных точках отрезка производные высших порядков по аналогии с первой производной определяются через значения односторонних производных таких же порядков.
Заметим, что у линейной функции 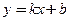 первая производная
первая производная 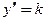 равна постоянной, а все последующие производные равны нулю:
равна постоянной, а все последующие производные равны нулю: 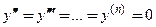 (
( . У квадратичной функции
. У квадратичной функции  первая производная
первая производная 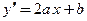 является линейной функцией, вторая производная
является линейной функцией, вторая производная 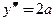 − постоянной, а все последующие производные, начиная с третьей производной, равны нулю. Обобщая наблюдения, можно доказать, что все производные многочлена п -й степени
− постоянной, а все последующие производные, начиная с третьей производной, равны нулю. Обобщая наблюдения, можно доказать, что все производные многочлена п -й степени  , начиная с производной
, начиная с производной 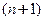 -го порядка, тождественно равны нулю:
-го порядка, тождественно равны нулю: 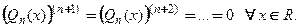
Механический смысл второй производной
Пусть 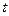 − время,
− время, 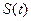 − путь, пройденный материальной точкой при прямолинейном движении за время
− путь, пройденный материальной точкой при прямолинейном движении за время 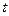 . В разделе 3.1.2 ускорение движения
. В разделе 3.1.2 ускорение движения  было определено как скорость изменения скорости движения и описано формулой
было определено как скорость изменения скорости движения и описано формулой 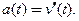 Так как
Так как 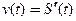 , то ускорение равно второй производной пути по времени:
, то ускорение равно второй производной пути по времени: 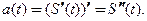
Ускорение является важной характеристикой движения. Если ускорение равно нулю на некотором временном промежутке, то движение − равномерное. Если ускорение является положительной фиксированной величиной на временном промежутке, то движение − равноускоренное; если ускорение − отрицательная фиксированная величина, то движение − равнозамедленное.
Вернемся к примеру 3.5, в котором путь, пройденный материальной точкой по прямой за время t, описывался формулой  . Ускорение движения
. Ускорение движения 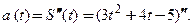 Первая производная пути по времени равна
Первая производная пути по времени равна 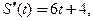 вторая производная
вторая производная  Значит, на всем пути ускорение постоянно:
Значит, на всем пути ускорение постоянно: 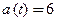 . Так как
. Так как  , то движение − равноускоренное.
, то движение − равноускоренное.
Дифференциалы высших порядков
Продолжим изучение функции  , имеющей конечные производные до п- го порядка включительно в каждой точке промежутка
, имеющей конечные производные до п- го порядка включительно в каждой точке промежутка 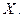 По теореме 3.3 эта функция дифференцируема на
По теореме 3.3 эта функция дифференцируема на 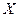 и ее дифференциал вычисляется по формуле
и ее дифференциал вычисляется по формуле  . Назовем его первым дифференциалом, или дифференциалом первого порядка. В частности, в точке
. Назовем его первым дифференциалом, или дифференциалом первого порядка. В частности, в точке 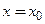 первый дифференциал равен
первый дифференциал равен 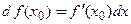 .
.
Дифференциалом 2-го порядка(вторым дифференциалом) функции  в точке
в точке 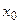 называется дифференциал первого дифференциала, который равен:
называется дифференциал первого дифференциала, который равен:  . Вычислим второй дифференциал в точке
. Вычислим второй дифференциал в точке 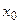 , полагая что
, полагая что  −
−
независимая переменная (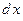 рассматриваем как постоянный множитель):
рассматриваем как постоянный множитель):  . Отсюда имеем:
. Отсюда имеем: 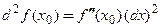 .
.
Если  − произвольная точка промежутка
− произвольная точка промежутка 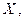 то
то 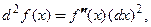 или
или 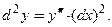 Тогда
Тогда 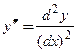 . Получено соотношение, которое использовали для обозначения второй производной.
. Получено соотношение, которое использовали для обозначения второй производной.
Дифференциалом 3-го порядка(третьим дифференциалом) функции  в точке
в точке 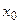 называется дифференциал второго дифференциала, который равен
называется дифференциал второго дифференциала, который равен 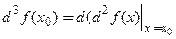 . Если
. Если 
 − независимая переменная, то
− независимая переменная, то 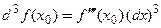 .
.
 Продолжим процедуру дифференцирования функции. Дифференциал дифференциала (
Продолжим процедуру дифференцирования функции. Дифференциал дифференциала (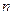 −1)-го порядка функции
−1)-го порядка функции  в точке
в точке 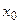 называют дифференциалом п-го порядка и обозначают
называют дифференциалом п-го порядка и обозначают  Отсюда, обобщая формулы для дифференциалов 2-го и 3-го, получим связь между производной и дифференциалом п- го порядка:
Отсюда, обобщая формулы для дифференциалов 2-го и 3-го, получим связь между производной и дифференциалом п- го порядка: 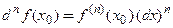 . Эту формулу для дифференциала п- го порядка можно компактно записать в виде
. Эту формулу для дифференциала п- го порядка можно компактно записать в виде
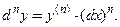 (3.14)
(3.14)
Отсюда
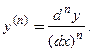 (3.15)
(3.15)
Таким образом, выражение 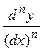 является не только обозначением производной п- го порядка, но и в случае независимой переменной х формулой для нахождения п- й производной как частного п- го дифференциала и п- й степени дифференциала
является не только обозначением производной п- го порядка, но и в случае независимой переменной х формулой для нахождения п- й производной как частного п- го дифференциала и п- й степени дифференциала 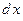 :
:  Можно доказать, что дифференциалы высших порядков
Можно доказать, что дифференциалы высших порядков 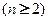 в общем случае не обладают инвариантным свойством в отличие от дифференциалов 1-го порядка.
в общем случае не обладают инвариантным свойством в отличие от дифференциалов 1-го порядка.
Функцию, имеющую дифференциалы до 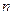 -го порядка включительно в точке
-го порядка включительно в точке 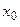 , называют
, называют 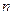 раз дифференцируемой в этой точке. Функцию,
раз дифференцируемой в этой точке. Функцию, 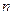 раз дифференцируемую в каждой точке промежутка, называют
раз дифференцируемую в каждой точке промежутка, называют 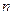 раз дифференцируемой на этом промежутке.
раз дифференцируемой на этом промежутке.
Пример 3.17. Найти третью производную 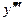 и третий дифференциал
и третий дифференциал  функции
функции 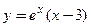 и вычислить их в точке
и вычислить их в точке 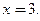
□ Сначала найдем все производные до третьего порядка включительно:
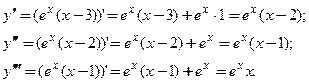
Потом по формуле (3.14) при 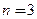 получим:
получим: 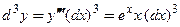 .
.
Подставляя  в выражения для
в выражения для 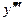 и
и  , имеем:
, имеем: 
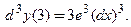 В точке
В точке  третья производная равна числу, а третий дифференциал является степенной функцией дифференциала
третья производная равна числу, а третий дифференциал является степенной функцией дифференциала 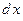 . ■
. ■
Пример 3.18. Вывести формулу для производной п- го порядка 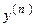 функции
функции 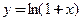 .
.
□ Выполним последовательное дифференцирование функции при  :
:  ;
;
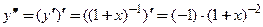 ;
;
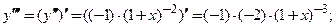

В результате получим 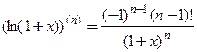 ,
, 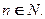 ■
■



 , заданную явно и имеющую конечную производную
, заданную явно и имеющую конечную производную  в любой точке
в любой точке  промежутка
промежутка 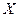 . Если функция
. Если функция  имеет производную (конечную или бесконечную) в каждой точке
имеет производную (конечную или бесконечную) в каждой точке 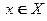 , то эту производную называют производной 2-го порядка (второй производной) функции
, то эту производную называют производной 2-го порядка (второй производной) функции  и обозначают
и обозначают 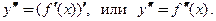
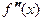 имеет производную
имеет производную 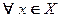 , то ее производная называется производной 3-го порядка (третьей производной):
, то ее производная называется производной 3-го порядка (третьей производной): 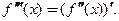 Аналогично берутся производные более высоких порядков.
Аналогично берутся производные более высоких порядков.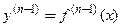 , то производная n-го порядка по определению равна производной от производной
, то производная n-го порядка по определению равна производной от производной  -го порядка:
-го порядка: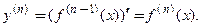 (3.13)
(3.13) . Таким образом, допустимы следующие значения числа п: 0; 1; 2;…; k;… Производные, порядки которых больше единицы (
. Таким образом, допустимы следующие значения числа п: 0; 1; 2;…; k;… Производные, порядки которых больше единицы ( ), называют производными высших порядков.
), называют производными высших порядков.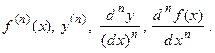 Круглые скобки в знаменателе обычно не пишут. Если порядок производной − конкретное число, то его обозначают штрихами (для производных до третьего порядка включительно), а также записывают римской цифрой без скобок или арабской в скобках:
Круглые скобки в знаменателе обычно не пишут. Если порядок производной − конкретное число, то его обозначают штрихами (для производных до третьего порядка включительно), а также записывают римской цифрой без скобок или арабской в скобках:
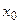 существует, то ее значение − число (собственное (конечное) или несобственное
существует, то ее значение − число (собственное (конечное) или несобственное 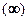 ), которое обозначается одним из следующих способов:
), которое обозначается одним из следующих способов: 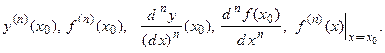
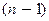 -го порядка включительно. Это утверждение можно доказать, опираясь на теорему 3.2.
-го порядка включительно. Это утверждение можно доказать, опираясь на теорему 3.2.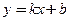 первая производная
первая производная 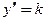 равна постоянной, а все последующие производные равны нулю:
равна постоянной, а все последующие производные равны нулю: 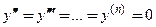 (
( . У квадратичной функции
. У квадратичной функции  первая производная
первая производная 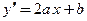 является линейной функцией, вторая производная
является линейной функцией, вторая производная 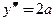 − постоянной, а все последующие производные, начиная с третьей производной, равны нулю. Обобщая наблюдения, можно доказать, что все производные многочлена п -й степени
− постоянной, а все последующие производные, начиная с третьей производной, равны нулю. Обобщая наблюдения, можно доказать, что все производные многочлена п -й степени  , начиная с производной
, начиная с производной 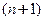 -го порядка, тождественно равны нулю:
-го порядка, тождественно равны нулю: 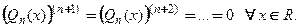
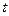 − время,
− время, 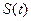 − путь, пройденный материальной точкой при прямолинейном движении за время
− путь, пройденный материальной точкой при прямолинейном движении за время  было определено как скорость изменения скорости движения и описано формулой
было определено как скорость изменения скорости движения и описано формулой 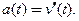 Так как
Так как 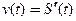 , то ускорение равно второй производной пути по времени:
, то ускорение равно второй производной пути по времени: 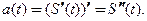
 . Ускорение движения
. Ускорение движения 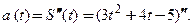 Первая производная пути по времени равна
Первая производная пути по времени равна 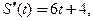 вторая производная
вторая производная  Значит, на всем пути ускорение постоянно:
Значит, на всем пути ускорение постоянно: 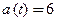 . Так как
. Так как  , то движение − равноускоренное.
, то движение − равноускоренное.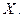 По теореме 3.3 эта функция дифференцируема на
По теореме 3.3 эта функция дифференцируема на  . Назовем его первым дифференциалом, или дифференциалом первого порядка. В частности, в точке
. Назовем его первым дифференциалом, или дифференциалом первого порядка. В частности, в точке 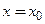 первый дифференциал равен
первый дифференциал равен 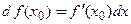 .
. . Вычислим второй дифференциал в точке
. Вычислим второй дифференциал в точке 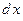 рассматриваем как постоянный множитель):
рассматриваем как постоянный множитель):  . Отсюда имеем:
. Отсюда имеем: 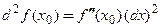 .
.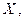 то
то 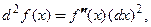 или
или 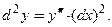 Тогда
Тогда 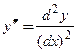 . Получено соотношение, которое использовали для обозначения второй производной.
. Получено соотношение, которое использовали для обозначения второй производной.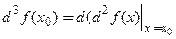 . Если
. Если 
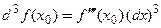 .
.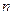 −1)-го порядка функции
−1)-го порядка функции  Отсюда, обобщая формулы для дифференциалов 2-го и 3-го, получим связь между производной и дифференциалом п- го порядка:
Отсюда, обобщая формулы для дифференциалов 2-го и 3-го, получим связь между производной и дифференциалом п- го порядка: 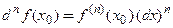 . Эту формулу для дифференциала п- го порядка можно компактно записать в виде
. Эту формулу для дифференциала п- го порядка можно компактно записать в виде 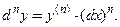 (3.14)
(3.14)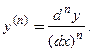 (3.15)
(3.15)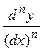 является не только обозначением производной п- го порядка, но и в случае независимой переменной х формулой для нахождения п- й производной как частного п- го дифференциала и п- й степени дифференциала
является не только обозначением производной п- го порядка, но и в случае независимой переменной х формулой для нахождения п- й производной как частного п- го дифференциала и п- й степени дифференциала  Можно доказать, что дифференциалы высших порядков
Можно доказать, что дифференциалы высших порядков 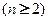 в общем случае не обладают инвариантным свойством в отличие от дифференциалов 1-го порядка.
в общем случае не обладают инвариантным свойством в отличие от дифференциалов 1-го порядка.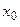 , называют
, называют 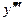 и третий дифференциал
и третий дифференциал  функции
функции 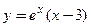 и вычислить их в точке
и вычислить их в точке 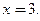
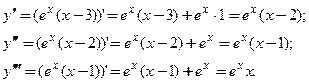
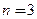 получим:
получим: 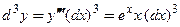 .
. в выражения для
в выражения для 
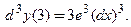 В точке
В точке 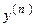 функции
функции 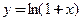 .
. :
:  ;
;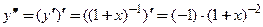 ;
;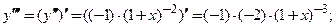

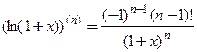 ,
, 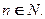 ■
■


