P (| X – M (X) | ≥ a) <  .
.
Пример 2. Пусть случайная величина Х имеет дисперсию D (X) = 0,001. Какова вероятность того, что
она отличается от М (Х) более чем на 0,1?
Согласно неравенству Чебышёва: P (| X – M (X) | ≥ 0,1) <  =
= 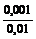 = 0,1.
= 0,1.
Пример 3. Дискретная случайная величина Х задана законом распределения
Используя неравенство Чебышёва, оценить вероятность того, что | X – M (X) | < 0,2.
М (Х) = 0,3 × 0,2 + 0,6 × 0,8 = 0,54.
|
| Х 2
| 0,09
| 0,36
| M (X 2) = 0,09 × 0,2 + 0,36 × 0,8 = 0,306.
|
|
| Р
| 0,2
| 0,8
|
D (Х) = M (X 2) – [ М (Х)]2 = 0,3024 – 0,542 = 0,306 – 0,2916 = 0,0144.
Воспользуемся неравенством Чебышёва в форме P (| X – M (X) | < ε) ≥ 1 – 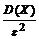 :
:
P (| X – 0,54 | < 0,2) ≥ 1 – 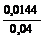 = 0,64.
= 0,64.
6.1.2. Закон больших чисел в форме Чебышёва (теорема Чебышёва)
Если случайные величины Х 1, Х 2, …, Х n, … попарно независимы и их дисперсии ограничены, D (Х n) ≤ C  n, то
n, то  ε > 0 справедливо:
ε > 0 справедливо:
 P
P 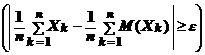 = 0 .
= 0 .
Здесь утверждается, что с ростом количества случайных величин их среднее арифметическое сколь угодно мало отличается от детерминированного, неслучайного воздействия, обусловленного средним арифметическим математических ожиданий.
Пример 4. Последовательность независимых случайных величин Х 1, Х 2, …, Х n, … задана законом распределения
Применима ли к данной последовательности теорема Чебышёва?
Для того чтобы к последовательности случайных величин была применима теорема Чебышева, достаточно, чтобы эти величины были попарно независимы и имели бы ограниченные дисперсии.
Т.к. случайные величины независимы, то они подавно и попарно независимы.
Для нахождения дисперсий найдем сначала мат.ожидание М (Х n):
М (Х n) = – na ×  + 0 ×
+ 0 ×  + na ×
+ na ×  = 0.
= 0.
Далее построим законы распределения случайных величин  :
:
М ( ) = n 2 a 2 ×
) = n 2 a 2 ×  + 0 ×
+ 0 ×  + n 2 a 2 ×
+ n 2 a 2 ×  = a 2.
= a 2.
D (Х n) = М ( ) – [ М (Х n)]2 = a 2 – 02 = a 2. Т. о., D (Х n) ≤ a 2
) – [ М (Х n)]2 = a 2 – 02 = a 2. Т. о., D (Х n) ≤ a 2  n.
n.
Все условия теоремы Чебышева выполнены и, следовательно, в данном случае она применима.
Пример 5. Вероятность появления события A в каждом из 400 проведенных испытаний равна 0,7. Найти с использованием неравенства Чебышева вероятность того, что число X появлений события A будет заключено в пределах от 260 до 300.
Воспользуемся неравенством Чебышева вида P (| X – M (X) | < ε) ≥ 1 – 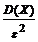 . Вычислив M (X)= np =400 · 0,7=280, D (X) = npq = 400 · 0,7 · 0,3 = 84, получаем P (260 < X < 300) = P (| X – 280 | < 20) ≥ 1 –
. Вычислив M (X)= np =400 · 0,7=280, D (X) = npq = 400 · 0,7 · 0,3 = 84, получаем P (260 < X < 300) = P (| X – 280 | < 20) ≥ 1 – 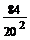 =0,79.
=0,79.
Пример 6. Математическое ожидание случайной величины X равно M (X) = 95, а дисперсия – D (X) = 9. Найти с использованием неравенства Чебышева вероятность того, что 90 < X < 100
P (| X – M (X) | < ε) ≥ 1 – 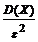 => Тогда P (90 < X < 100)= P (| X – 95| < 5) ≥ 1 –
=> Тогда P (90 < X < 100)= P (| X – 95| < 5) ≥ 1 –  =0,64.
=0,64.
В приложениях важную роль играет частный случай приведенной выше теоремы,
относящийся к одинаково распределенным независимым слагаемым:
Пусть Х 1, Х 2, …, Х n, … – одинаково распределенные случайные величины с
M (Х n) = m  n. Тогда
n. Тогда
 P
P 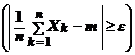 = 0 .
= 0 .
Другим важным следствием теоремы Чебышева является теорема Я.Бернулли.
6.1.3. Закон больших чисел в форме Бернулли (теорема Бернулли)
Пусть S n – число успехов в серии изn независимых испытаний с постоянной вероятностью успеха р в каждом испытании и ν n =  – относительная частота числа успехов. Тогда с увеличением количества экспериментов n частота ν n будет мало отличаться от вероятности р. Точнее,
– относительная частота числа успехов. Тогда с увеличением количества экспериментов n частота ν n будет мало отличаться от вероятности р. Точнее,  P (| ν n – p | ≥ ε) = 0 .
P (| ν n – p | ≥ ε) = 0 .
Предельные теоремы
Предельные теоремы дают представление о законе распределения суммы большого
числа случайных величин.
Центральная предельная теорема (ЦПТ). Если последовательность попарно
независимых случайных величин Х 1, Х 2, …, Х n, … удовлетворяет условию
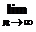
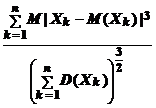 = 0, (1)
= 0, (1)
то 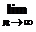 Р
Р 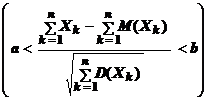 = Ф (b) – Ф (a). (2)
= Ф (b) – Ф (a). (2)
Здесь Ф (х) = 
 – функция Лапласа.
– функция Лапласа.
Условие (1) дано А.М. Ляпуновым. Поэтому приведенная теорема называется центральной предельной теоремой в форме Ляпунова. Есть и другие формулировки центральной предельной теоремы. Отличаются они тем, что условие (1) в них заменено другим, имеющим тот же смысл. Смысл условия (1), и других аналогичных условий, состоит в следующем: в сумме  ни одно из слагаемых не доминирует, т.е. вклад в сумму каждогослагаемого не подавляет вклада остальных слагаемых.
ни одно из слагаемых не доминирует, т.е. вклад в сумму каждогослагаемого не подавляет вклада остальных слагаемых.
Смысл равенства (2) в том, что при больших n случайная величина
Y = 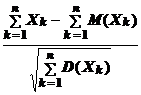 (3)
(3)
распределена по нормальному закону с нулевым (M (Y) = 0) математическим ожиданием и единичной (D (Y) = 1) дисперсией. Эту случайную величину называют нормированной.



 .
. =
= 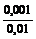 = 0,1.
= 0,1.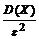 :
: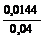 = 0,64.
= 0,64. n, то
n, то  P
P 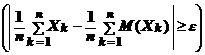 = 0 .
= 0 .
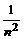
 + na ×
+ na ×  :
:
 ) – [ М (Х n)]2 = a 2 – 02 = a 2. Т. о., D (Х n) ≤ a 2
) – [ М (Х n)]2 = a 2 – 02 = a 2. Т. о., D (Х n) ≤ a 2  n.
n.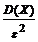 . Вычислив M (X)= np =400 · 0,7=280, D (X) = npq = 400 · 0,7 · 0,3 = 84, получаем P (260 < X < 300) = P (| X – 280 | < 20) ≥ 1 –
. Вычислив M (X)= np =400 · 0,7=280, D (X) = npq = 400 · 0,7 · 0,3 = 84, получаем P (260 < X < 300) = P (| X – 280 | < 20) ≥ 1 – 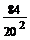 =0,79.
=0,79.  =0,64.
=0,64. 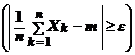 = 0 .
= 0 . – относительная частота числа успехов. Тогда с увеличением количества экспериментов n частота ν n будет мало отличаться от вероятности р. Точнее,
– относительная частота числа успехов. Тогда с увеличением количества экспериментов n частота ν n будет мало отличаться от вероятности р. Точнее, 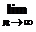
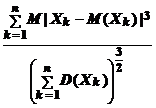 = 0, (1)
= 0, (1)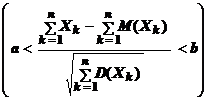 = Ф (b) – Ф (a). (2)
= Ф (b) – Ф (a). (2)
 – функция Лапласа.
– функция Лапласа. ни одно из слагаемых не доминирует, т.е. вклад в сумму каждогослагаемого не подавляет вклада остальных слагаемых.
ни одно из слагаемых не доминирует, т.е. вклад в сумму каждогослагаемого не подавляет вклада остальных слагаемых. 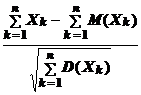 (3)
(3)


