Умножение, и особенно деление комплексных чисел чаще всего бывает легче выполнять в тригонометрической форме, чем в алгебраической, так как для деления не нужно домножать на сопряжённое в знаменателе.
Формула: 
Доказательство.
 =
= 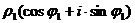
 =
=
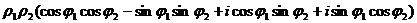 =
=
используем известные тригонометрические формулы косинуса суммы и синуса суммы, и получим  .
.
Таким образом, для умножения двух комплексных чисел, представленных в тригонометрической форме, достаточно просто умножить их модули и сложить аргументы.
Заметим, что при умножении на мнимую единицу 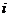 , а именно при действии
, а именно при действии 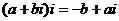 , фактически вектор
, фактически вектор 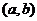 на плоскости переходит в
на плоскости переходит в  , то есть как раз и прибавляется аргумент числа
, то есть как раз и прибавляется аргумент числа 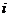 , то есть 90 0.
, то есть 90 0.
Примеры.
Умножить 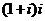 . Во-первых, это можно сделать и без триг.формы:
. Во-первых, это можно сделать и без триг.формы:
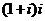 =
= 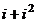 =
= 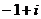 .
.
В тригонометрической форме: (используем представление чисел, которое сделали ранее).
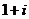 =
=  .
. 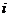 =
= 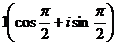 .
.
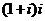 =
= 
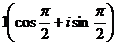 =
=
 =
= 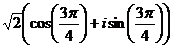 =
=
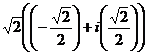 =
= 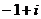 .
.
 =
= 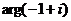 .
.
Формула деления двух комплексных чисел в тригонометрической форме: 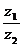 =
= 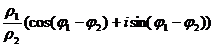 .
.
Для её доказательства достаточно домножить на 
 :
:
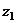 =
=  =
=  =
=
 .
.
Для деления двух комплексных чисел, представленных в тригонометрической форме, нужно поделить их модули и вычесть аргументы.
Поделить  .
.
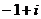 =
= 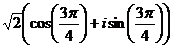 ,
, 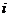 =
= 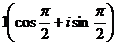 . Тогда
. Тогда
 =
=  =
=
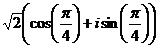 =
=  =
= 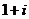 .
.
Формула Эйлера 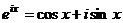
Доказательство.
Способ 1. 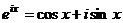
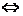

Производная по 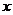 :
:
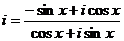 =
=  =
=  .
.
Способ 2. Разложение экспоненты по формуле Тейлора:
 Тогда
Тогда 
Но  ,
, 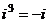 ,
,  ,...
,...
Тогда  теперь соберём в отдельные слагаемые все части, где нет
теперь соберём в отдельные слагаемые все части, где нет 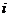 , и где есть
, и где есть 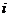 .
.
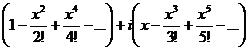
в 1 и 2 скобках - разложения 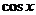 и
и 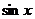 . Итак,
. Итак, 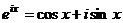 , что и требовалось доказать.
, что и требовалось доказать.
Показательная форма комплексного числа.
По формуле Эйлера, выражение  может быть записано в виде
может быть записано в виде  .
.
Так, например, мнимой единице соответствует аргумент 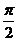 и модуль 1, поэтому запись в тригонометрической и показательной формах такова:
и модуль 1, поэтому запись в тригонометрической и показательной формах такова: 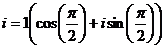
 .
.
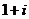 =
= 
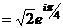
Умножение и деление в показательной форме.
В показательной форме.

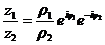 =
= 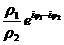 .
.
Пример. Поделить  .
.
Решение.  =
= 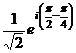 =
= 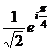 =
=  =
=
 =
=  .
.
Формула Муавра, степень. Корни.
Возводить комплексные числа в степень можно с помощью такой формулы: 
она называется формулой Муавра и позволяет не перемножать множество скобок, если требуется вычислить большую степень числа.
Доказательство. Если умножим в тригонометрической форме не два разных числа, а одно и то же число 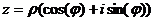 , то получим:
, то получим:
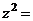
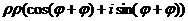 =
=  .
.
Таким же образом можно умножить 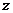 в третий раз и снова в аргументе прибавится
в третий раз и снова в аргументе прибавится  , а модуль снова умножится на
, а модуль снова умножится на  .
.

 =
=
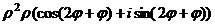 =
= 
Таким образом, по индукции, можно доказать, что
 =
= 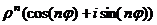 .
.
Но ещё легче возводить в степень с помощью показательной формы числа:  , здесь даже доказывать по индукции нет необходимости.
, здесь даже доказывать по индукции нет необходимости.
Пример. Найти  по формуле Муавра.
по формуле Муавра.
Вычислим модуль и аргумент. 
 .
.
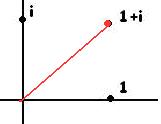
По формуле Муавра,  =
=  =
=  = 16.
= 16.
В показательной форме: 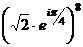 =
= 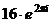 =
= 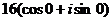 = 16.
= 16.
ЛЕКЦИЯ 14. 27.3.2021.
Степени комплексных чисел в тригонометрической форме можно использовать для выведения различных формул тригонометрии, например, двойных и кратных углов.
Для степени 2:
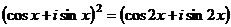 , так как угол удваивается.
, так как угол удваивается.
С другой стороны, можем просто раскрыть скобки при возведении в квадрат:  =
=
 . Сравнивая отдельно действительные и мнимые части, получим хорошо известные формулы:
. Сравнивая отдельно действительные и мнимые части, получим хорошо известные формулы:
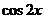 =
= 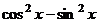 ,
,  =
=  .
.
Для степени 3:
 , по формуле Муавра.
, по формуле Муавра.
с другой стороны, раскроем простым умножением, как в биноме Ньютона:
 =
=
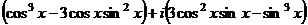 .
.
Совпадают комплексные величины, значит, совпадают их действительные и мнимые части. Приравняем их:
 =
= 
 =
= 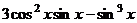
Впрочем, далее можно в тех местах, где квадрат синуса или косинуса, представить через основное триг. тождество, чтобы выразить через одну и ту же функцию:
 =
= 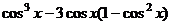 =
= 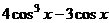 ,
,
 =
=  =
=  .
.
Корни степени n. Корни степени n вычисляются по формуле:

 .
.
Доказательство. Если возведём в степень n, получим  =
=  .
.
Получается, что добавка 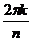 после возведения в степень станет кратной
после возведения в степень станет кратной 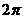 , то есть точка, отстоящая на угол
, то есть точка, отстоящая на угол 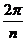 , просто опишет один лишний оборот вокруг начала координат, то есть к аргументу добавится 3600, и придёт в ту же точку, что и было бы без
, просто опишет один лишний оборот вокруг начала координат, то есть к аргументу добавится 3600, и придёт в ту же точку, что и было бы без 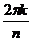 .
.
При  получается n разных точек.
получается n разных точек.
Докажем, что таким образом найдены все корни, и не существует какого-либо другого 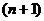 -го корня при каком-либо другом
-го корня при каком-либо другом 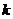 .
.
Возьмём  . Тогда число
. Тогда число 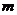 можно поделить на
можно поделить на  (возможно, с остатком), а именно,
(возможно, с остатком), а именно,  , где
, где  . Рассмотрим выражение
. Рассмотрим выражение
 =
=
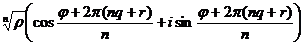 =
=
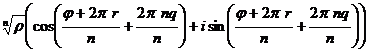 =
=
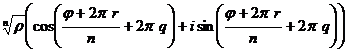 =
=
 , где
, где  ,
,
то есть нет нового корня, он совпадает с каким-то из ранее найденных.
Замечание.  , два значения, частный случай.
, два значения, частный случай.
 =
= 
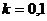 .
.
Две точки на окружности – через 180 град. Eсли число было положительным, то его аргумент был 0, и тогда по формуле 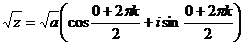 то есть
то есть
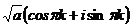 =
=  =
= 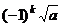 , что и соответствует
, что и соответствует  при
при 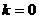 и
и  . К аргументу прибавляется по 360 / 2 = 180 градусов.
. К аргументу прибавляется по 360 / 2 = 180 градусов.
Пример. Найдите все значения корня  .
.
Сначала представим комплексное число, которое находится под знаком корня, в тригонометрической форме.
Точка расположена на мнимой оси выше начала координат, поэтому аргумент 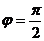 , модуль
, модуль  .
.
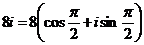 - представление в триг. форме.
- представление в триг. форме.
Теперь находим все 3 корня.
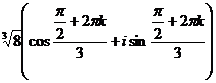 при k = 0,1,2.
при k = 0,1,2. 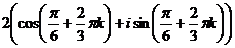 , отсюда:
, отсюда:
1) k=0: 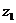 =
=  =
= 
2) k=1: 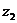 =
=  =
= 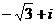
3) k=2:  =
= 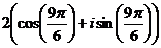 =
= 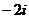
Чертёж:
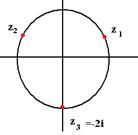
Если к исходному углу добавить 120 градусов, то для куба этого числа добавится 360 градусов, и результат будет точно такой же. С этим фактом как раз и связано наличие лишнего слагаемого 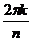 в формуле.
в формуле.
Квадратные корни из -1:
 ,
,
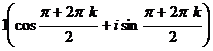 =
= 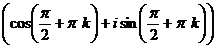 ,
,
Углы 90 и 270 град.
1) k=0 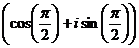 =
= 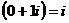
2) k=1  =
= 
- - - Перерыв - - -
Корни из единицы.
Так как 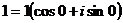 , то корни из 1 имеют вид:
, то корни из 1 имеют вид:

Само число 1, очевидно является корнем любой степени n из 1, и это значение получается при 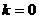 . Обозначим этот корень
. Обозначим этот корень 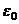 ,
,
 ,
, 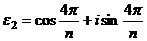 ,...
,...
Множество корней из 1 обозначим:  .
.

Теорема 1. 1) 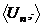 абелева группа.
абелева группа.
2) 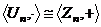 , группа корней степени n из единицы изоморфна аддтитивной группе вычетов по модулю n.
, группа корней степени n из единицы изоморфна аддтитивной группе вычетов по модулю n.
Доказательство.
1) Так как  - кольцо, то
- кольцо, то 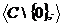 - абелева группа, причём
- абелева группа, причём  . Тогда достаточно доказать, что
. Тогда достаточно доказать, что 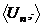 подгруппа в
подгруппа в 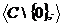 с помощью критерия подгруппы.
с помощью критерия подгруппы.
Пусть  - два различных корня. Покажем, что
- два различных корня. Покажем, что  , то есть является каким-то корнем из 1.
, то есть является каким-то корнем из 1.
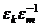 =
=  , поделим в тригонометрической форме,
, поделим в тригонометрической форме,
получим 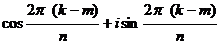 =
= 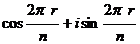 , а как доказано ранее, любое число такого вида совпадает с каким-либо из n корней из единицы (поделить с остатком, получить на месте
, а как доказано ранее, любое число такого вида совпадает с каким-либо из n корней из единицы (поделить с остатком, получить на месте 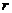 число из множества
число из множества 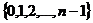 ).
).
2) Изоморфизм 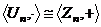 можем задать так:
можем задать так: 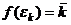 .
.

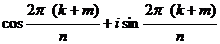 =
= 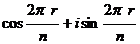 , где
, где  ,
, 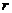 остаток от деления на
остаток от деления на  , если
, если 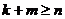 , и
, и 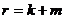 если
если 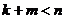 . При этом верно и
. При этом верно и  в группе вычетов (если
в группе вычетов (если 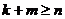 , то класс вычетов определяется остатком от деления на
, то класс вычетов определяется остатком от деления на  ).
).
Определение. Группа 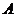 называется циклической, если существует элемент
называется циклической, если существует элемент 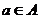 , такой, что любой элемент из
, такой, что любой элемент из 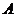 является его степенью. В этом случае говорят, что группа порождается элементом
является его степенью. В этом случае говорят, что группа порождается элементом 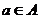 , обозначение
, обозначение 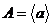 .
.
Лемма. 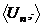 - циклическая группа.
- циклическая группа.
Доказательство. Для всякого 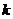 ,
, 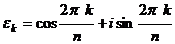 =
=
 .
.
Определение. Корень  -й степени из 1 называется первообразным, если он не является корнем из 1 с меньшим, чем
-й степени из 1 называется первообразным, если он не является корнем из 1 с меньшим, чем  , натуральным показателем, то есть
, натуральным показателем, то есть  , но ни при каком
, но ни при каком  :
: 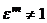 .
.
Пример. 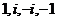 корни 4 степени из 1. Но
корни 4 степени из 1. Но 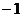 и 1 ещё и в квадрате, а не только в 4 степени, равны 1, то есть для
и 1 ещё и в квадрате, а не только в 4 степени, равны 1, то есть для  . А вот корни
. А вот корни  первообразные.
первообразные.
Лемма. Корень 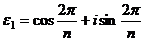 первообразный для любого n.
первообразный для любого n.
Док-во: при  ,
, 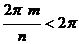 , и это число в степени
, и это число в степени 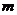 не может быть = 1.
не может быть = 1.
Теорема 2. Число 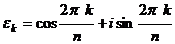 есть первообразный корень
есть первообразный корень  -й степени из 1
-й степени из 1 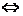
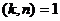 (взаимно просты).
(взаимно просты).




 =
= 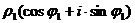
 =
=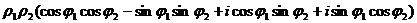 =
=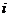 , а именно при действии
, а именно при действии 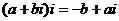 , фактически вектор
, фактически вектор 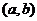 на плоскости переходит в
на плоскости переходит в  , то есть как раз и прибавляется аргумент числа
, то есть как раз и прибавляется аргумент числа 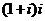 . Во-первых, это можно сделать и без триг.формы:
. Во-первых, это можно сделать и без триг.формы: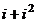 =
= 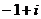 .
. 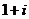 =
=  .
. 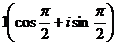 .
. =
= 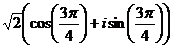 =
=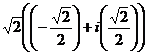 =
=  =
= 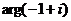 .
.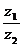 =
= 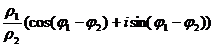 .
.
 :
: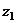 =
=  =
=  =
= .
.  .
. =
=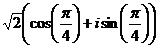 =
=  =
= 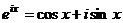
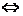

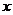 :
: 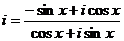 =
=  =
=  .
.  Тогда
Тогда 
 ,
, 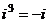 ,
,  ,...
,... теперь соберём в отдельные слагаемые все части, где нет
теперь соберём в отдельные слагаемые все части, где нет 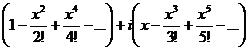
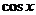 и
и 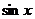 . Итак,
. Итак,  может быть записано в виде
может быть записано в виде  .
.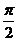 и модуль 1, поэтому запись в тригонометрической и показательной формах такова:
и модуль 1, поэтому запись в тригонометрической и показательной формах такова: 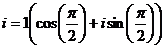
 .
.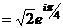

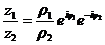 =
= 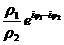 .
.  .
. =
= 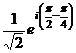 =
= 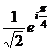 =
=  =
=  =
=  .
.
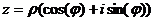 , то получим:
, то получим: 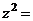
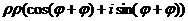 =
=  .
.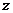 в третий раз и снова в аргументе прибавится
в третий раз и снова в аргументе прибавится  , а модуль снова умножится на
, а модуль снова умножится на  .
. =
=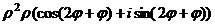 =
= 
 =
= 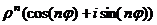 .
.  , здесь даже доказывать по индукции нет необходимости.
, здесь даже доказывать по индукции нет необходимости. по формуле Муавра.
по формуле Муавра.
 .
.
 =
=  =
=  = 16.
= 16.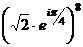 =
= 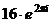 =
= 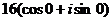 = 16.
= 16.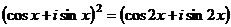 , так как угол удваивается.
, так как угол удваивается. =
= . Сравнивая отдельно действительные и мнимые части, получим хорошо известные формулы:
. Сравнивая отдельно действительные и мнимые части, получим хорошо известные формулы: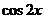 =
= 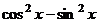 ,
,  =
=  .
.  , по формуле Муавра.
, по формуле Муавра. =
=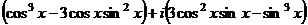 .
.  =
= 
 =
= 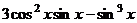
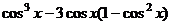 =
= 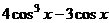 ,
,  =
=  .
. 
 .
.  =
=  .
.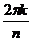 после возведения в степень станет кратной
после возведения в степень станет кратной 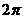 , то есть точка, отстоящая на угол
, то есть точка, отстоящая на угол 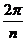 , просто опишет один лишний оборот вокруг начала координат, то есть к аргументу добавится 3600, и придёт в ту же точку, что и было бы без
, просто опишет один лишний оборот вокруг начала координат, то есть к аргументу добавится 3600, и придёт в ту же точку, что и было бы без 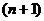 -го корня при каком-либо другом
-го корня при каком-либо другом 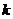 .
.  . Тогда число
. Тогда число 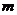 можно поделить на
можно поделить на  (возможно, с остатком), а именно,
(возможно, с остатком), а именно,  , где
, где  . Рассмотрим выражение
. Рассмотрим выражение =
=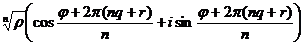 =
=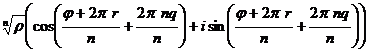 =
=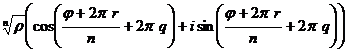 =
= , где
, где  , два значения, частный случай.
, два значения, частный случай. =
= 
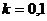 .
.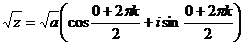 то есть
то есть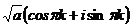 =
=  =
= 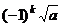 , что и соответствует
, что и соответствует  при
при 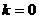 и
и  . К аргументу прибавляется по 360 / 2 = 180 градусов.
. К аргументу прибавляется по 360 / 2 = 180 градусов.  .
.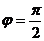 , модуль
, модуль  .
.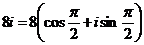 - представление в триг. форме.
- представление в триг. форме.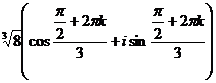 при k = 0,1,2.
при k = 0,1,2. 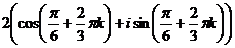 , отсюда:
, отсюда: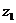 =
=  =
= 
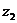 =
=  =
= 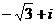
 =
= 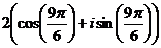 =
= 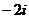

 ,
,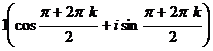 =
= 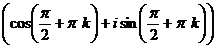 ,
,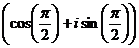 =
= 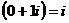
 =
= 
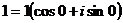 , то корни из 1 имеют вид:
, то корни из 1 имеют вид: 
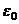 ,
,  ,
, 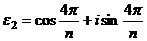 ,...
,... .
.
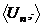 абелева группа.
абелева группа.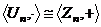 , группа корней степени n из единицы изоморфна аддтитивной группе вычетов по модулю n.
, группа корней степени n из единицы изоморфна аддтитивной группе вычетов по модулю n.  - кольцо, то
- кольцо, то 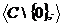 - абелева группа, причём
- абелева группа, причём  . Тогда достаточно доказать, что
. Тогда достаточно доказать, что  - два различных корня. Покажем, что
- два различных корня. Покажем, что  , то есть является каким-то корнем из 1.
, то есть является каким-то корнем из 1.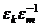 =
=  , поделим в тригонометрической форме,
, поделим в тригонометрической форме,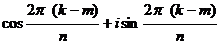 =
= 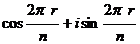 , а как доказано ранее, любое число такого вида совпадает с каким-либо из n корней из единицы (поделить с остатком, получить на месте
, а как доказано ранее, любое число такого вида совпадает с каким-либо из n корней из единицы (поделить с остатком, получить на месте 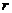 число из множества
число из множества 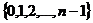 ).
).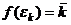 .
. 
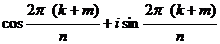 =
=  ,
, 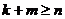 , и
, и 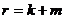 если
если 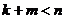 . При этом верно и
. При этом верно и  в группе вычетов (если
в группе вычетов (если 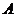 называется циклической, если существует элемент
называется циклической, если существует элемент 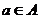 , такой, что любой элемент из
, такой, что любой элемент из 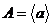 .
.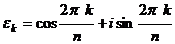 =
= .
.  , но ни при каком
, но ни при каком  :
: 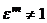 .
.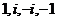 корни 4 степени из 1. Но
корни 4 степени из 1. Но 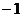 и 1 ещё и в квадрате, а не только в 4 степени, равны 1, то есть для
и 1 ещё и в квадрате, а не только в 4 степени, равны 1, то есть для  первообразные.
первообразные.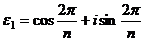 первообразный для любого n.
первообразный для любого n.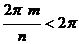 , и это число в степени
, и это число в степени 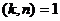 (взаимно просты).
(взаимно просты). 


