

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
ЛЕКЦИЯ 13. 25.3.2021.
Поле комплексных чисел.
Поле действительных чисел не содержит корни некоторых многочленов, например  . В общем случае, если уравнение
. В общем случае, если уравнение 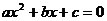 имеет отрицательный дискриминант, т.е.
имеет отрицательный дискриминант, т.е.  , то на действительной оси корней нет. Существует система обобщённых чисел, где и такие уравнения тоже имеют решения. Комплексные числа геометрически соответствуют точкам на плоскости, где действительная ось - это горизонтальная ось Ох в данной плоскости. «Мнимая единица»
, то на действительной оси корней нет. Существует система обобщённых чисел, где и такие уравнения тоже имеют решения. Комплексные числа геометрически соответствуют точкам на плоскости, где действительная ось - это горизонтальная ось Ох в данной плоскости. «Мнимая единица»  «квадратный корень из минус 1». При этом
«квадратный корень из минус 1». При этом  .
.

Горизонтальная ось отождествляется со множеством действительных чисел, а мнимая ось, содержащая  , перпендикулярна оси действительных чисел.
, перпендикулярна оси действительных чисел.
Числовые множества: 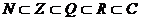 .
.
Каждой точке на плоскости с координатами 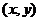 можно поставить в соответствие комплексное число, состоящее из действительной и мнимой части:
можно поставить в соответствие комплексное число, состоящее из действительной и мнимой части:  . Проекция на действительную и мнимую ось называются действительной частью и мнимой частью комплексного числа.
. Проекция на действительную и мнимую ось называются действительной частью и мнимой частью комплексного числа.  ,
, 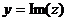 .
.
Если  , то число
, то число 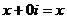 это действительное число.
это действительное число.
Сложение и вычитание комплексных чисел определяется покоординатно, как для обычных векторов в плоскости.
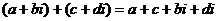 =
= 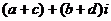 .
.
Для вычитания аналогично:  =
= 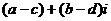 .
.
Умножение.
 =
= 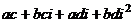 , учитывая тот факт, что
, учитывая тот факт, что  ,
,
получаем  =
= 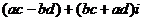 .
.
Таким образом, после раскрытия скобок, надо просто учесть  и привести подобные.
и привести подобные.
Пример. 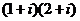 =
=  =
= 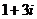 .
.
Определение. число  называется сопряжённым к
называется сопряжённым к  .
.
Умножим два взаимно сопряжённых комплексных числа:
 =
= 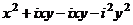 =
= 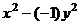 =
= 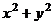 , получилось действительное число. Мы заметили, что при умножении на сопряжённое мнимая часть станет 0. Этот факт можно использовать для процедуры деления. Если домножить на сопряжённое в знаменателе, то там получится действительное число, и это даст возможность разбить на сумму двух дробей. При этом, конечно, в числителе тоже домножаем на сопряжённое к знаменателю, чтобы дробь не изменилась.
, получилось действительное число. Мы заметили, что при умножении на сопряжённое мнимая часть станет 0. Этот факт можно использовать для процедуры деления. Если домножить на сопряжённое в знаменателе, то там получится действительное число, и это даст возможность разбить на сумму двух дробей. При этом, конечно, в числителе тоже домножаем на сопряжённое к знаменателю, чтобы дробь не изменилась.
|
|
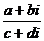 =
= 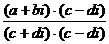 =
=  =
= 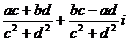
Обозначения 
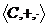
Теорема. 1) 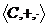 является полем.
является полем.
2)  является подполем поля
является подполем поля 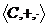 .
.
Доказательство. 1)
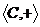 - абелева группа. Коммутативность и ассоциативность по сложению очевидна, нейтральный элемент
- абелева группа. Коммутативность и ассоциативность по сложению очевидна, нейтральный элемент 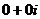 , противоположный
, противоположный 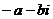 .
.
Коммутативность по умножению:


Ассоциативность по умножению:
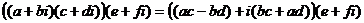 =
=
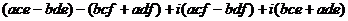 .
.
 =
=
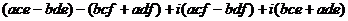 .
.
Нейтральный элемент по умножению 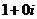 :
:
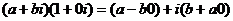 =
=  .
.
Для любого числа, кроме 0, существует обратное:
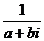 =
= 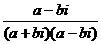 =
=  =
= 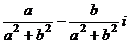 .
.
Дистрибутивность.
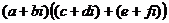 =
=  =
=
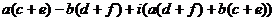 =
=
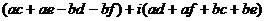 .
.
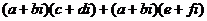 =
=
 =
=
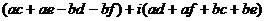 .
.
2) Поле действительных чисел является подполем (см. критерий подполя: разность 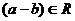 и
и  , если
, если 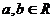 ).
).
Лемма. Поле комплексных чисел изоморфно полю матриц вида  .
.
Доказательство. Рассмотрим отображение 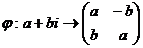 и докажем, что это изоморфизм.
и докажем, что это изоморфизм. 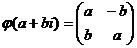 ,
,  .
.
Докажем, что сумма комплексных чисел соответствует сумме матриц, а произведение - произведению матриц.

 =
= 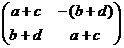 .
.

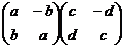 =
= 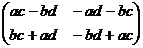 .
.
Замечание. Обратный элемент тоже можно искать с помощью матриц, обратной матрицы. 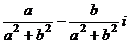
Определитель  ,
,  .
.
Доказательство.
Сложим  и
и  .
.
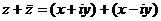 =
=  , тогда
, тогда 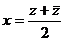 .
.
Вычтем  и
и  .
.
 =
=  , тогда
, тогда 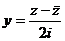 .
.
- - - Перерыв - - -
Тригонометрическая форма комплексного числа. Введём величину  тогда
тогда 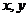 можно представить в таком виде:
можно представить в таком виде:  ,
, 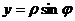 (вспомнить: полярные координаты) для некоторого
(вспомнить: полярные координаты) для некоторого  , ведь геометрически в этом случае
, ведь геометрически в этом случае 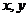 - катеты прямоугольного треугольника,
- катеты прямоугольного треугольника,  - его гипотенуза. Заметим, что
- его гипотенуза. Заметим, что  .
.
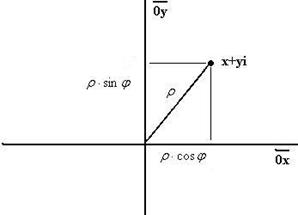
Абсцисса и ордината точки 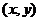 на плоскости это проекции на оси, они равны
на плоскости это проекции на оси, они равны  и
и 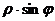 соответственно. Эти величины
соответственно. Эти величины  и
и  и есть полярные координаты точки на плоскости. Если записать комплексное число
и есть полярные координаты точки на плоскости. Если записать комплексное число 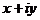 с помощью введённых выше величин
с помощью введённых выше величин  и
и  , получим:
, получим: 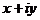 =
= 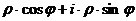 =
=  .
.
Выражение  называется тригонометрической формой комплексного числа,
называется тригонометрической формой комплексного числа,  - его аргументом,
- его аргументом,  - модулем.
- модулем.

 .
.
Понятие модуля согласуется с известным понятием, применявшимся раньше для отрицательных чисел: модуль - расстояние по кратчайшей линии до начала координат.
|
|
Для любой точки 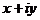 модуль вычисляется как
модуль вычисляется как  . Для вычисления аргумента верна формула
. Для вычисления аргумента верна формула 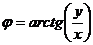 если точка в 4-й и 1-й четверти, либо
если точка в 4-й и 1-й четверти, либо  , если во 2-й и 3-й четверти.
, если во 2-й и 3-й четверти.
Так, число 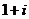 запишется в виде
запишется в виде 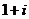 =
=  .
.
Число 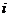 =
= 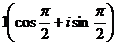 .
.

Если вычислить синус и косинус, то снова перейдём к обычной, «алгебраической» форме числа:
 =
= 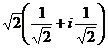 =
= 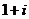 .
.
Действительное число имеет аргумент 0 (если оно положительно) или  (если оно отрицательно).
(если оно отрицательно).
Угол может определяться разными способами, так, например, вместо угла  во всех вычислениях для комплексных чисел в тригонометрической форме можно использовать
во всех вычислениях для комплексных чисел в тригонометрической форме можно использовать 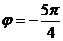 , и это не будет ошибкой, так как тригонометрические функции повторяются через промежуток
, и это не будет ошибкой, так как тригонометрические функции повторяются через промежуток 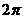 .
.
Доказательство.
 =
= 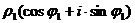
 =
=
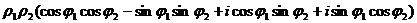 =
=
используем известные тригонометрические формулы косинуса суммы и синуса суммы, и получим  .
.
Примеры.
Умножить 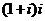 . Во-первых, это можно сделать и без триг.формы:
. Во-первых, это можно сделать и без триг.формы:
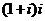 =
= 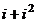 =
= 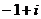 .
.
В тригонометрической форме: (используем представление чисел, которое сделали ранее).
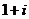 =
=  .
. 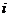 =
= 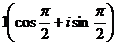 .
.
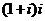 =
= 
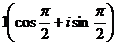 =
=
 =
= 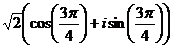 =
=
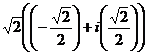 =
= 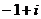 .
.
 =
= 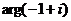 .
.
Формула деления двух комплексных чисел в тригонометрической форме: 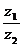 =
= 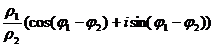 .
.
Для её доказательства достаточно домножить на 
 :
:
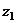 =
=  =
=  =
=
 .
.
Доказательство.
Способ 1. 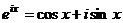
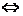

Производная по 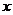 :
:
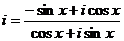 =
=  =
=  .
.
Способ 2. Разложение экспоненты по формуле Тейлора:
 Тогда
Тогда 
Но  ,
, 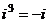 ,
,  ,...
,...
Тогда  теперь соберём в отдельные слагаемые все части, где нет
теперь соберём в отдельные слагаемые все части, где нет 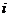 , и где есть
, и где есть 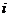 .
.
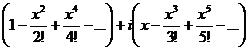
в 1 и 2 скобках - разложения 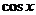 и
и 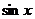 . Итак,
. Итак, 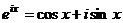 , что и требовалось доказать.
, что и требовалось доказать.
ЛЕКЦИЯ 14. 27.3.2021.
Степени комплексных чисел в тригонометрической форме можно использовать для выведения различных формул тригонометрии, например, двойных и кратных углов.
Для степени 2:
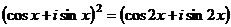 , так как угол удваивается.
, так как угол удваивается.
С другой стороны, можем просто раскрыть скобки при возведении в квадрат:  =
=
 . Сравнивая отдельно действительные и мнимые части, получим хорошо известные формулы:
. Сравнивая отдельно действительные и мнимые части, получим хорошо известные формулы:
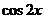 =
= 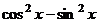 ,
,  =
=  .
.
Для степени 3:
 , по формуле Муавра.
, по формуле Муавра.
с другой стороны, раскроем простым умножением, как в биноме Ньютона:
 =
=
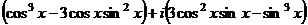 .
.
Совпадают комплексные величины, значит, совпадают их действительные и мнимые части. Приравняем их:
 =
= 
 =
= 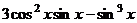
Впрочем, далее можно в тех местах, где квадрат синуса или косинуса, представить через основное триг. тождество, чтобы выразить через одну и ту же функцию:
 =
= 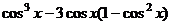 =
= 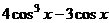 ,
,
|
|
 =
=  =
=  .
.
Корни степени n. Корни степени n вычисляются по формуле:

 .
.
Доказательство. Если возведём в степень n, получим  =
=  .
.
Получается, что добавка 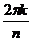 после возведения в степень станет кратной
после возведения в степень станет кратной 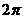 , то есть точка, отстоящая на угол
, то есть точка, отстоящая на угол 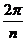 , просто опишет один лишний оборот вокруг начала координат, то есть к аргументу добавится 3600, и придёт в ту же точку, что и было бы без
, просто опишет один лишний оборот вокруг начала координат, то есть к аргументу добавится 3600, и придёт в ту же точку, что и было бы без 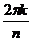 .
.
При  получается n разных точек.
получается n разных точек.
Докажем, что таким образом найдены все корни, и не существует какого-либо другого 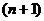 -го корня при каком-либо другом
-го корня при каком-либо другом 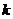 .
.
Возьмём  . Тогда число
. Тогда число 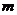 можно поделить на
можно поделить на  (возможно, с остатком), а именно,
(возможно, с остатком), а именно,  , где
, где  . Рассмотрим выражение
. Рассмотрим выражение
 =
=
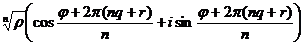 =
=
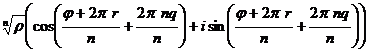 =
=
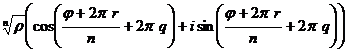 =
=
 , где
, где  ,
,
то есть нет нового корня, он совпадает с каким-то из ранее найденных.
Замечание.  , два значения, частный случай.
, два значения, частный случай.
 =
= 
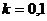 .
.
Две точки на окружности – через 180 град. Eсли число было положительным, то его аргумент был 0, и тогда по формуле 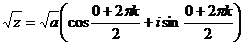 то есть
то есть
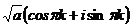 =
=  =
= 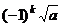 , что и соответствует
, что и соответствует  при
при 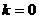 и
и  . К аргументу прибавляется по 360 / 2 = 180 градусов.
. К аргументу прибавляется по 360 / 2 = 180 градусов.
Пример. Найдите все значения корня  .
.
Сначала представим комплексное число, которое находится под знаком корня, в тригонометрической форме.
Точка расположена на мнимой оси выше начала координат, поэтому аргумент 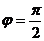 , модуль
, модуль  .
.
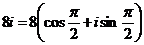 - представление в триг. форме.
- представление в триг. форме.
Теперь находим все 3 корня.
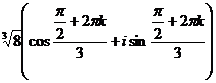 при k = 0,1,2.
при k = 0,1,2. 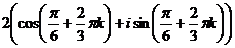 , отсюда:
, отсюда:
1) k=0: 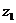 =
=  =
= 
2) k=1: 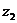 =
=  =
= 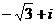
3) k=2:  =
= 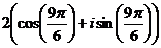 =
= 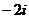
Чертёж:
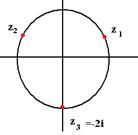
Если к исходному углу добавить 120 градусов, то для куба этого числа добавится 360 градусов, и результат будет точно такой же. С этим фактом как раз и связано наличие лишнего слагаемого 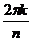 в формуле.
в формуле.
Квадратные корни из -1:
 ,
,
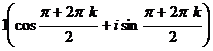 =
= 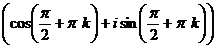 ,
,
Углы 90 и 270 град.
1) k=0 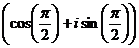 =
= 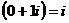
2) k=1  =
= 
- - - Перерыв - - -
Корни из единицы.
Так как 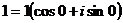 , то корни из 1 имеют вид:
, то корни из 1 имеют вид:

Само число 1, очевидно является корнем любой степени n из 1, и это значение получается при 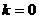 . Обозначим этот корень
. Обозначим этот корень 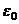 ,
,
 ,
, 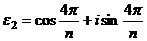 ,...
,...
Множество корней из 1 обозначим:  .
.

Теорема 1. 1) 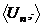 абелева группа.
абелева группа.
2) 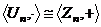 , группа корней степени n из единицы изоморфна аддтитивной группе вычетов по модулю n.
, группа корней степени n из единицы изоморфна аддтитивной группе вычетов по модулю n.
Доказательство.
1) Так как  - кольцо, то
- кольцо, то 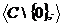 - абелева группа, причём
- абелева группа, причём  . Тогда достаточно доказать, что
. Тогда достаточно доказать, что 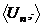 подгруппа в
подгруппа в 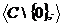 с помощью критерия подгруппы.
с помощью критерия подгруппы.
|
|
Пусть  - два различных корня. Покажем, что
- два различных корня. Покажем, что  , то есть является каким-то корнем из 1.
, то есть является каким-то корнем из 1.
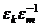 =
=  , поделим в тригонометрической форме,
, поделим в тригонометрической форме,
получим 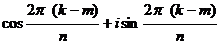 =
= 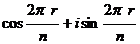 , а как доказано ранее, любое число такого вида совпадает с каким-либо из n корней из единицы (поделить с остатком, получить на месте
, а как доказано ранее, любое число такого вида совпадает с каким-либо из n корней из единицы (поделить с остатком, получить на месте 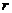 число из множества
число из множества 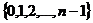 ).
).
2) Изоморфизм 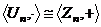 можем задать так:
можем задать так: 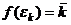 .
.

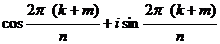 =
= 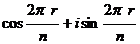 , где
, где  ,
, 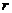 остаток от деления на
остаток от деления на  , если
, если 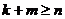 , и
, и 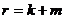 если
если 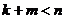 . При этом верно и
. При этом верно и  в группе вычетов (если
в группе вычетов (если 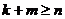 , то класс вычетов определяется остатком от деления на
, то класс вычетов определяется остатком от деления на  ).
).
Определение. Группа 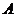 называется циклической, если существует элемент
называется циклической, если существует элемент 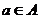 , такой, что любой элемент из
, такой, что любой элемент из 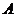 является его степенью. В этом случае говорят, что группа порождается элементом
является его степенью. В этом случае говорят, что группа порождается элементом 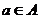 , обозначение
, обозначение 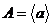 .
.
Лемма. 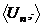 - циклическая группа.
- циклическая группа.
Доказательство. Для всякого 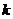 ,
, 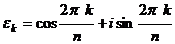 =
=
 .
.
Определение. Корень  -й степени из 1 называется первообразным, если он не является корнем из 1 с меньшим, чем
-й степени из 1 называется первообразным, если он не является корнем из 1 с меньшим, чем  , натуральным показателем, то есть
, натуральным показателем, то есть  , но ни при каком
, но ни при каком  :
: 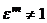 .
.
Пример. 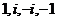 корни 4 степени из 1. Но
корни 4 степени из 1. Но 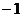 и 1 ещё и в квадрате, а не только в 4 степени, равны 1, то есть для
и 1 ещё и в квадрате, а не только в 4 степени, равны 1, то есть для  . А вот корни
. А вот корни  первообразные.
первообразные.
Лемма. Корень 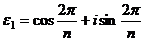 первообразный для любого n.
первообразный для любого n.
Док-во: при  ,
, 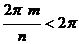 , и это число в степени
, и это число в степени 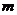 не может быть = 1.
не может быть = 1.
Теорема 2. Число 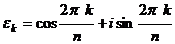 есть первообразный корень
есть первообразный корень  -й степени из 1
-й степени из 1 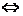
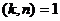 (взаимно просты).
(взаимно просты).
ЛЕКЦИЯ 15. 1.4.2021
Лемма. Сумма всех корней степени  из 1 равна 0.
из 1 равна 0.
Доказательство. Пусть 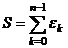 .
.
Но 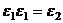 ,
, 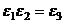 ,...,
,..., 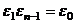 (при умножении на
(при умножении на 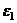 каждая точка поворачивается на угол
каждая точка поворачивается на угол 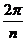 и переходит в следующую).
и переходит в следующую).
Тогда 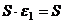 , так как это сумма тех же
, так как это сумма тех же  комплексных чисел. Но при этом
комплексных чисел. Но при этом 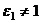 . Значит,
. Значит, 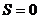 .
.
Доказательство.
Рассмотрим для действительного числа 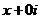 и покажем, что данные функции, а именно
и покажем, что данные функции, а именно 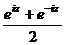 и
и 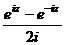 , приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,
, приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус. Используя формулу Эйлера,
1) 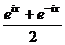 =
= 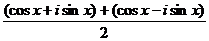 =
= 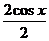 =
= 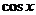
2) 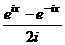 =
=  =
= 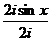 =
= 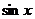
Неограниченность синуса и косинуса в комплексной плоскости.
Пример. 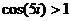 .
.
Вычислим: 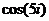 =
= 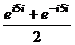 =
= 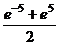
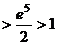 .
.
Логарифм комплексного числа.
Обобщённый логарифм вводится с помощью формулы:
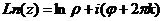 (
(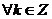 )
)
Доказательство.
Проверим, совпадает ли 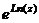 и
и 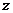 при любом целом
при любом целом 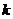 .
.
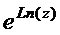 =
=  =
= 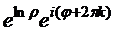 =
= 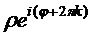 =
=
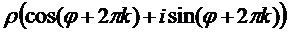 =
=
синус и косинус не зависят от прибавления угла, кратного 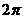 , поэтому получаем
, поэтому получаем 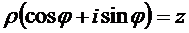 .
.
А это уже и есть тригонометрическая форма комплексного числа.
Итак, 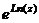 =
= 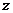 .
.
Если вычислять логарифм положительного действительного числа, то 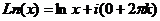 , т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол
, т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол 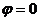 . Для любого числа, которое не является действительным положительным,
. Для любого числа, которое не является действительным положительным, 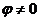 , поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.
, поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.
Пример. Вычислить 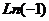 .
.
Здесь 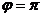 ,
, 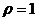 . Поэтому
. Поэтому 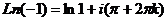 =
= 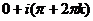 .
.
Точки в комплексной плоскости: 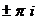 ,
, 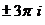 ,
, 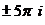 , и так далее.
, и так далее.
|
|
Ни одного значения на действительной оси нет, и здесь, по сравнению со значениями логарифма положительного числа, сдвиг на половину деления: одна точка ушла вверх с действительной оси, а другая ещё не достигла этой оси. Чертёж:
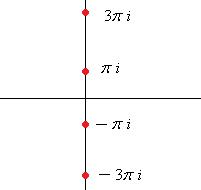
Здесь легко сделать и проверку: 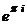 =
= 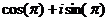 =
= 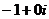 =
= 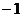 , то есть действительно,
, то есть действительно, 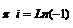 .
.
Пример. Вычислить 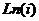 .
.
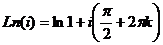 =
= 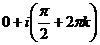 . Последовательность значений такова:
. Последовательность значений такова: 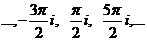 каждая соседняя пара отличается на
каждая соседняя пара отличается на 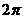 по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для
по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для 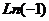 .
.
1) При фиксированном модуле исходного числа и увеличении его аргумента, эта последовательность точек плывёт вверх, при полном повороте на 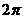 как раз следующая точка попадёт на место предыдущей.
как раз следующая точка попадёт на место предыдущей.
2) При фиксированном аргументе исходного числа и увеличении его модуля, эта последовательность точек плывёт вправо, если исходная точка внутри единичной окружности то множество значений логарифма в левой полуплоскости, так как 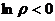 , а если вне единичной окружности, то в правой полуплоскости.
, а если вне единичной окружности, то в правой полуплоскости.
Динамическая анимация, показывающая поведение значений 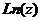 в зависимости от колебаний модуля или аргумента
в зависимости от колебаний модуля или аргумента 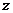 , показана в следующем обучающем видеоролике:
, показана в следующем обучающем видеоролике:
http://www.youtube.com/watch?v=LKFFn-TSLd0
Замечание. Единственная точка в комплексной плоскости, для которой не существует логарифма, это 0. Ведь в этом случае 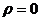 , и не существует
, и не существует 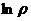 .
.
Пример. Вычислить 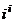 .
.
Решение. Представим 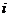 , расположенную в основании, в виде
, расположенную в основании, в виде 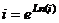 . Тогда
. Тогда 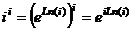 , причём чуть выше мы вычисляли
, причём чуть выше мы вычисляли
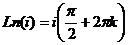 . Тогда
. Тогда 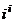 =
= 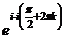 =
= 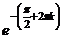 т.е. получается бесконечное множество точек на действительной оси.
т.е. получается бесконечное множество точек на действительной оси.
Для всякой функции 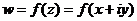 можно отдельно выделить действительную и мнимую части, и представить в виде
можно отдельно выделить действительную и мнимую части, и представить в виде
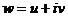 . Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения:
. Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения: 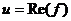 ,
, 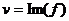 . Итак, комплексной функции можно поставить в соответствие некоторое отображение из
. Итак, комплексной функции можно поставить в соответствие некоторое отображение из 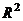 в
в 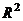 , а именно
, а именно 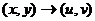 . Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.
. Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.
Пример. Разложить 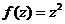 на сумму действительной и мнимой частей, изобразить искажения плоскости при переходе
на сумму действительной и мнимой частей, изобразить искажения плоскости при переходе 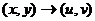 .
.
1) 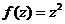 =
= 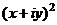 =
= 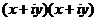 =
= 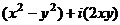 .
.
Таким образом, 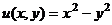 ,
, 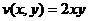 .
.
Чтобы исследовать, куда переходят горизонтальные прямые, зафиксируем 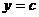 , при этом
, при этом 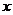 изменяется от
изменяется от 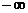 до
до 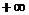 , пусть движение задано с помощью параметра
, пусть движение задано с помощью параметра 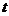 :
:
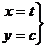
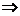
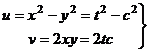 .
.
Чтобы составить уравнение, взаимосвязывающее 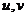 , и узнать, какая это кривая, исключим параметр
, и узнать, какая это кривая, исключим параметр 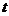 , выразив из второго уравнения:
, выразив из второго уравнения: 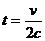 , тогда
, тогда 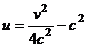 . Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше
. Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше 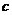 , тем левее вершина, и тем более пологая парабола получается, ведь
, тем левее вершина, и тем более пологая парабола получается, ведь 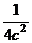 при этом меньше. А если
при этом меньше. А если 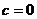 , то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости
, то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости 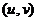 .
.
Аналогично, для какой-либо вертикальной прямой:
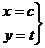
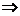
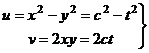 . Тогда, исключая параметр
. Тогда, исключая параметр 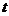 , получим
, получим 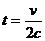
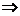
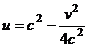 . Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.
. Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.
На чертеже зелёным цветом показаны горизонтальные прямые и их образы при отображении 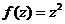 , а красным - вертикальные прямые и их образы:
, а красным - вертикальные прямые и их образы:
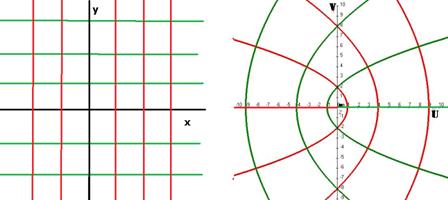
Примечание. 4-мерный график можно было бы рассматривать таким образом: нужно как минимум 4 проекции на координатные пространства, а именно 0xyz, 0xzw, 0xyw, 0yzw.
Либо можно рассмотреть 2 поверхности, построенные по функциям 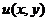 и
и 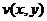 .
.
Линейные пространства над С
Над полем комплексных чисел тоже, как и над R, можно рассматривать линейные пространства различной размерности. Рассмотрим, чем отличается строение скалярного произведения в этом случае, и каким будет аналог евклидового пространства.
Напомним, что в линейном пространстве 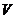 над полем
над полем 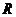 задано евклидово скалярное произведение, если задана функция
задано евклидово скалярное произведение, если задана функция  , т.е. каждой паре векторов можно однозначно поставить в соответствие число
, т.е. каждой паре векторов можно однозначно поставить в соответствие число 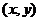 , причём:
, причём:
1) 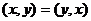
2) 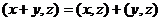 ,
, 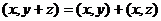
3)

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!