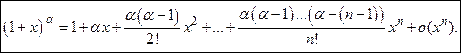Выведем формулы для вычисления дифференциалов высших порядков:
 , то есть
, то есть
 .
.
Аналогично вычисляется дифференциал любого 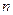 −го порядка:
−го порядка:
 .
.
Дифференциалы сложной функции
Приведенные выше формулы справедливы только, если 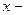 независимая переменная. Теперь рассмотрим случай, когда
независимая переменная. Теперь рассмотрим случай, когда 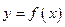 , где
, где  зависимая переменная. Тогда функция
зависимая переменная. Тогда функция 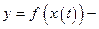 сложная функция аргумента
сложная функция аргумента  и для ее дифференциала получим:
и для ее дифференциала получим:
 .
.
Форма дифференциала первого порядка 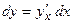 имеет один и тот же вид (то есть инвариантна ) и в случае, когда
имеет один и тот же вид (то есть инвариантна ) и в случае, когда 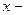 зависимое переменное, и в случае, когда
зависимое переменное, и в случае, когда 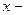 независимое переменное.
независимое переменное.
Теоремы о среднем
Теоремы Ролля, Лагранжа, Коши
Рассмотрим ряд теорем, имеющих большое теоретическое и прикладное значение. В их формулировке фигурирует некоторая «средняя» точка, поэтому их называют теоремами о среднем. Иногда, в силу их значимости, эти теоремы называют основными теоремами дифференциального исчисления.
Теорема Ролля. Пусть функция 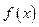
1) непрерывна на отрезке  2) дифференцируема на интервале
2) дифференцируема на интервале  ,
,
3) на концах отрезка принимает равные значения 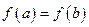 .
.
Тогда найдется хотя бы одна точка  , в которой производная
, в которой производная  обращается в нуль, т.е.
обращается в нуль, т.е.  .
.
Теорема Лагранжа. Пусть функция 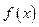 непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале  . Тогда найдется хотя бы одна точка
. Тогда найдется хотя бы одна точка  такая, что
такая, что
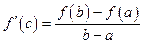 или
или 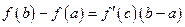 .
.
.
Следствие. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке.
Теорема Коши. Пусть функции 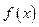 и
и 
1) непрерывны на отрезке  2) дифференцируемы на интервале
2) дифференцируемы на интервале  ,
,
3) 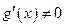 на
на  . Тогда найдется хотя бы одна точка
. Тогда найдется хотя бы одна точка  такая, что
такая, что
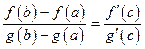 .
.
.
9.2.Правило Лопиталя
Правило Лопиталя применяется для раскрытия неопределенностей вида  или
или  с использованием производных и выводится с помощью рассмотренной теоремы Коши.
с использованием производных и выводится с помощью рассмотренной теоремы Коши.
Теорема Лопиталя. Пусть 1) в выколотой окрестности точки  функции
функции  дифференцируемы и
дифференцируемы и 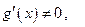 2) существует
2) существует  .
.
Тогда, в случае неопределенности  или
или  , справедливо правило Лопиталя:
, справедливо правило Лопиталя:
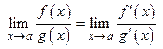 .
.
Формула Тейлора
Во многих прикладных задачах требуется заменить сложную функцию  многочленом
многочленом  , близким к
, близким к  в окрестности точки
в окрестности точки  ,в том смысле, что
,в том смысле, что
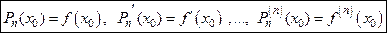 .
.
Введем ряд понятий.
1). Многочлен  , удовлетворяющий условию (9.3), называется многочленом Тейлора
, удовлетворяющий условию (9.3), называется многочленом Тейлора  −го порядка функции
−го порядка функции  в окрестности точки
в окрестности точки  .
.
2). Разность между функцией  и её многочленом Тейлора
и её многочленом Тейлора  обозначают
обозначают  :
: 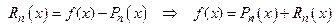 .
.
3). Формула  , где
, где  −многочлен Тейлора, называется формулой Тейлора n -го порядка для функции
−многочлен Тейлора, называется формулой Тейлора n -го порядка для функции  ,
,  называется остаточным членом формулы Тейлора.
называется остаточным членом формулы Тейлора.
Теорема 9.1 (о виде многочлена Тейлора).
Пусть функция  дифференцируема
дифференцируема 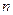 раз в окрестности точки
раз в окрестности точки  . Тогда многочлен Тейлора
. Тогда многочлен Тейлора 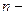 го порядка функции
го порядка функции  имеет вид:
имеет вид:
 .
.
Используя вид многочлена Тейлора, запишем формулу Тейлора 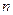 − го порядка:
− го порядка:
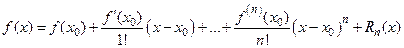 .
.
При  формула Тейлора называется формулой Маклорена и имеет вид:
формула Тейлора называется формулой Маклорена и имеет вид:
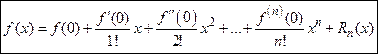
Рассмотрим вид остаточного члена  формулы Тейлора.
формулы Тейлора.
Теорема 9.2(об остаточном члене в форме Пеано).
Пусть функция  дифференцируема
дифференцируема 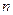 раз в окрестности точки
раз в окрестности точки  . Тогда остаточный член формулы Тейлора имеет вид:
. Тогда остаточный член формулы Тейлора имеет вид:
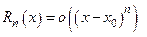 при
при  .
.
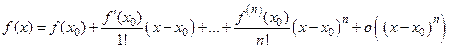 .
.
Эту формулу будем называть асимптотическим разложением  го порядка функции
го порядка функции 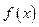 в окрестности точки
в окрестности точки  .
.
Теорема 9.3 (об остаточном члене в форме Лагранжа).
Пусть функция  дифференцируема
дифференцируема  раз в окрестности точки
раз в окрестности точки  . Тогда остаточный член формулы Тейлора в этой окрестности можно записать в форме
. Тогда остаточный член формулы Тейлора в этой окрестности можно записать в форме
 , (9.10)
, (9.10)
где 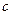 – некоторая точка между
– некоторая точка между  и
и  .
.
Асимптотические разложения
Элементарных функций
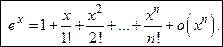
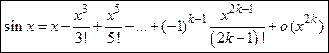 .
.
 .
.
 .
.
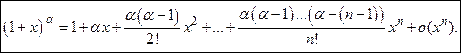




 , то есть
, то есть .
. 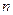 −го порядка:
−го порядка: .
. 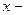 независимая переменная. Теперь рассмотрим случай, когда
независимая переменная. Теперь рассмотрим случай, когда 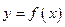 , где
, где  зависимая переменная. Тогда функция
зависимая переменная. Тогда функция 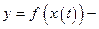 сложная функция аргумента
сложная функция аргумента  и для ее дифференциала получим:
и для ее дифференциала получим: .
.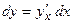 имеет один и тот же вид (то есть инвариантна ) и в случае, когда
имеет один и тот же вид (то есть инвариантна ) и в случае, когда 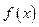
 2) дифференцируема на интервале
2) дифференцируема на интервале  ,
,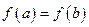 .
. , в которой производная
, в которой производная  обращается в нуль, т.е.
обращается в нуль, т.е.  .
. , дифференцируема на интервале
, дифференцируема на интервале 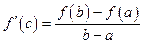 или
или 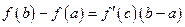 .
. 
 2) дифференцируемы на интервале
2) дифференцируемы на интервале 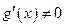 на
на 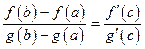 .
. или
или  с использованием производных и выводится с помощью рассмотренной теоремы Коши.
с использованием производных и выводится с помощью рассмотренной теоремы Коши. функции
функции  дифференцируемы и
дифференцируемы и 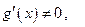 2) существует
2) существует  .
.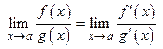 .
. многочленом
многочленом  , близким к
, близким к  ,в том смысле, что
,в том смысле, что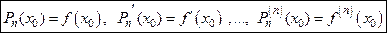 .
.  , удовлетворяющий условию (9.3), называется многочленом Тейлора
, удовлетворяющий условию (9.3), называется многочленом Тейлора  −го порядка функции
−го порядка функции  .
. :
: 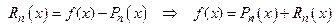 .
. , где
, где 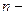 го порядка функции
го порядка функции  .
. 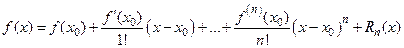 .
.  формула Тейлора называется формулой Маклорена и имеет вид:
формула Тейлора называется формулой Маклорена и имеет вид: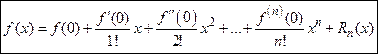
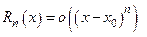 при
при  .
. 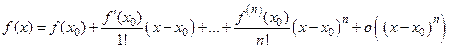 .
. го порядка функции
го порядка функции  раз в окрестности точки
раз в окрестности точки  , (9.10)
, (9.10)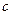 – некоторая точка между
– некоторая точка между  и
и 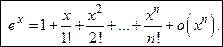
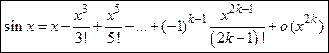 .
.  .
.  .
.