Предел и непрерывность функции одной переменной
Понятие предела является одним из важнейших понятий математического анализа. Основные понятия математического анализа, такие как производная, интеграл, связаны с предельным переходом.
Для сокращения записи мы будем использовать символы  − любой и
− любой и 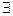 − существует. Запись
− существует. Запись  :
: 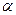 означает «для всякого элемента
означает «для всякого элемента  имеет место предложение
имеет место предложение 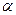 ». Запись
». Запись 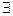
 :
: 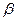 означает «существует элемент
означает «существует элемент  , для которого имеет место предложение
, для которого имеет место предложение 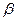 ». Запись
». Запись 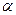

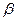 означает «из предложения
означает «из предложения 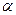 следует предложение
следует предложение 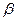 ». Запись
». Запись 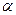

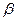 означает, что
означает, что 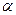 и
и 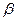 эквивалентны.
эквивалентны.
Для изучения пределов используется понятие окрестности точки.
Окрестности конечной точки и бесконечности
 1).
1). 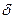 - окрестность конечной точки
- окрестность конечной точки  обозначим
обозначим  и определим как множество действительных чисел
и определим как множество действительных чисел 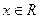 таких, что
таких, что  (рис.1):
(рис.1):
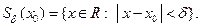
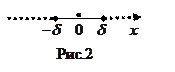 2).
2). 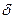 - окрестность бесконечности обозначим
- окрестность бесконечности обозначим  и определим как множество действительных чисел
и определим как множество действительных чисел 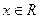 таких, что
таких, что 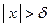 (рис.2). Итак,
(рис.2). Итак,

 .
.

3).
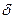
-
окрестность плюс бесконечности определим (рис.3) как

 4).
4). 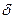 - окрестность минус бесконечности определим (рис 4) как
- окрестность минус бесконечности определим (рис 4) как
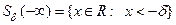 .
.
 5). Введём понятие выколотой окрестности
5). Введём понятие выколотой окрестности 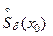 точки
точки  , которая получается из окрестности
, которая получается из окрестности  удалением точки
удалением точки  :
:

Определение предела функции
Предел функции на языке окрестностей
Рассмотрим функцию 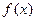 и предположим, что аргумент
и предположим, что аргумент  стремится к числу
стремится к числу 
 Если для всех
Если для всех  , достаточно близких к
, достаточно близких к  , соответствующие значения функции
, соответствующие значения функции 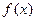 как угодно близки к числу
как угодно близки к числу 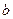 , то число
, то число  называют пределом функции
называют пределом функции 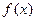 при
при  ; записывают это следующим образом:
; записывают это следующим образом:
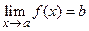 или
или  при
при  .
.
Определение предела функции (на языке окрестностей)
Число 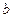 называется пределом функции
называется пределом функции 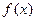 при
при 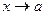 , если для любого положительного числа
, если для любого положительного числа  найдётся положительное число
найдётся положительное число  такое, что значения функции
такое, что значения функции 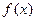 принадлежат
принадлежат  -окрестности точки
-окрестности точки 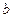 для всех
для всех  из выколотой
из выколотой  -окрестности точки
-окрестности точки 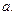
Это определение распространяется и на случаи, когда  и (или)
и (или)  − «несобственные числа»
− «несобственные числа» 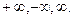 В дальнейшем это определение будем записывать кратко с помощью символов следующим образом:
В дальнейшем это определение будем записывать кратко с помощью символов следующим образом:
 если для
если для  такое, что
такое, что  для
для  3.2. Предел функции на языке неравенств
3.2. Предел функции на языке неравенств
Рассмотрим несколько случаев.
1). Пусть 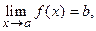
 и
и 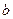 – конечные числа. Тогда
– конечные числа. Тогда
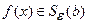 означает, что
означает, что  ;
;
 означает, что
означает, что 
и определение предела принимает вид:
 если для если для 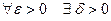 такое, что такое, что
 , как только , как только 
|
2). Пусть 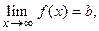
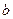 - конечное число. Тогда
- конечное число. Тогда
 означает, что
означает, что  ,
,
 означает, что
означает, что 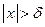
и определение предела принимает вид:
 если для если для 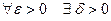 такое, что такое, что
 , как только , как только 
|
3). Пусть 
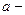 конечное число. Тогда
конечное число. Тогда
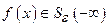 означает, что
означает, что  ,
,
 означает, что
означает, что 
и определение предела принимает вид:
 если для если для 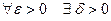 такое, что такое, что
 , как только , как только 
|
Предел последовательности
Числовая последовательность – это значения  функции натурального аргумента
функции натурального аргумента 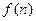 , расположенные в порядке возрастания аргумента
, расположенные в порядке возрастания аргумента
 …,
…,  …
…
Другое обозначение последовательности: 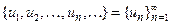 .
.
Примеры последовательностей:
1) 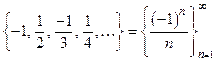 , 2)
, 2) 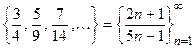 .
.
Предел последовательности можно рассматривать как частный случай предела функции, а именно функции натурального аргумента 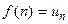 при
при 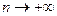 (обычно пишут
(обычно пишут  ), т.е.
), т.е.
Если предел последовательности существует и конечен, то последовательность называют сходящейся. Если предел последовательности не существует или бесконечен, то её называют расходящейся
Бесконечно малые функции
Отношение бесконечно малых.
Неопределенность 
В отличие от суммы и произведения, отношение бесконечно малых функций может иметь любой предел или даже его не иметь. Например, для функций 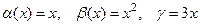 , являющихся бесконечно малыми при
, являющихся бесконечно малыми при 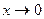 , имеем:
, имеем:
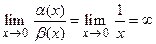 ,
, 
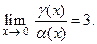
Поэтому отношение бесконечно малых функций называют неопределенностью вида  . Отыскание предела в случае неопределенности называют раскрытием неопределенности.
. Отыскание предела в случае неопределенности называют раскрытием неопределенности.
Первый замечательный предел
При вычислении пределов выражений, содержащих тригонометрические функции, часто используется 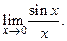 Он является неопределенностью
Он является неопределенностью  .
.
Покажем, что
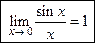 . (5.1)
. (5.1)
Это равенство называют первым замечательным пределом.
Следствие: 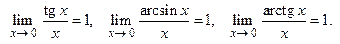
Сравнение бесконечно малых
Бесконечно малые функции часто сравнивают между собой по «быстроте» стремления к нулю. Так, например, из двух функций 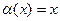 и
и  − бесконечно малых при
− бесконечно малых при  , функция
, функция  стремится к нулю «быстрее», чем
стремится к нулю «быстрее», чем  . Уточним, какой смысл вкладывается в слово «быстрее».
. Уточним, какой смысл вкладывается в слово «быстрее».
Пусть  и
и  бесконечно малые функции при
бесконечно малые функции при 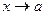 .
.
1). Если 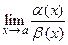 конечен и отличен от нуля, то
конечен и отличен от нуля, то  и
и 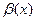 называют бесконечно малыми одного порядка и обозначают так:
называют бесконечно малыми одного порядка и обозначают так:  при
при  .
.
В частности, если  то
то  и
и 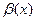 называют эквивалентными бесконечно малыми и обозначают так:
называют эквивалентными бесконечно малыми и обозначают так:  ~
~ 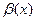 при
при  .
.
2). Если  то
то  называют бесконечно малой более высокого порядка, чем
называют бесконечно малой более высокого порядка, чем 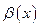 и обозначают так:
и обозначают так:  при
при  .
.
3). Если  то
то 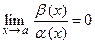 и
и 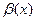 будет бесконечно малой более
будет бесконечно малой более
высокого порядка, чем  при
при  .
.
4). Если  не существует, то
не существует, то  и
и 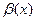 называют несравнимыми бесконечно малыми при
называют несравнимыми бесконечно малыми при  .
. 
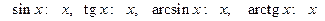 при при 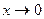 . .
|
Это вытекает из первого замечательного предела и его следствия.
Теорема 5.4 (об эквивалентных бесконечно малых).
Пусть 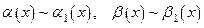 при при 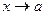 . Тогда . Тогда 
|
Бесконечно большие функции
Второй замечательный предел
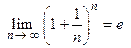 .
.
Число e – иррациональное, 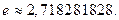
Это соотношение будет справедливо, если заменить натуральное число 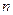 на действительное число
на действительное число  или на действительное число
или на действительное число  :
:
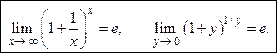
Непрерывные функции
Одной переменной
Дифференциальное исчисление функции одной переменной изучает одно из основных математических понятий  понятие производной и ее применение, в частности, для исследования функций.
понятие производной и ее применение, в частности, для исследования функций.
Производная и дифференциал
Понятие производной широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости протекания различных процессов.
Определение производной
Рассмотрим функцию 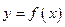 . Придадим аргументу
. Придадим аргументу  приращение
приращение 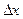 . Тогда функция
. Тогда функция 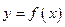 получит приращение
получит приращение  , которое характеризует изменение функции
, которое характеризует изменение функции 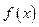 на отрезке
на отрезке 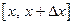 . Средняя скорость изменения функции на этом отрезке равна
. Средняя скорость изменения функции на этом отрезке равна  , а скорость изменения функции
, а скорость изменения функции 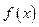 в точке
в точке  есть
есть 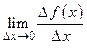 . Этот предел, если он существует, называется производной
. Этот предел, если он существует, называется производной  функции
функции 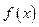 в точке
в точке  . Итак, по определению
. Итак, по определению

Для функции 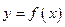 приняты и другие обозначения производной:
приняты и другие обозначения производной: 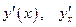 .
.
Производная сложной функции
Пусть 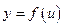 , а
, а 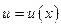 . Тогда
. Тогда 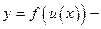 сложная функция с промежуточным аргументом
сложная функция с промежуточным аргументом 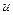 , независимым аргументом
, независимым аргументом  .
.
Теорема 8.3. Пусть функция 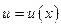 дифференцируема в точке
дифференцируема в точке  , а функция
, а функция 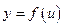 дифференцируема в соответствующей точке
дифференцируема в соответствующей точке 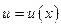 . Тогда сложная функция
. Тогда сложная функция 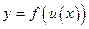 дифференцируема в точке
дифференцируема в точке  и для ее производной справедлива формула:
и для ее производной справедлива формула:  .
.
Итак, для нахождения производной сложной функции надо производную функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Это правило остается в силе, если промежуточных аргументов несколько.
Таблица производных
Рассмотренные правила и формулы дифференцирования запишем в виде таблицы.
Правила дифференцирования
1. 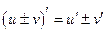 ,
,
2.  , в частности,
, в частности, 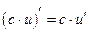 , где с − число,
, где с − число,
3.  , в частности,
, в частности, 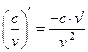 , где с − число,
, где с − число,
4.  , где
, где 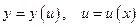 ,
,
5. 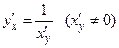 .
.
Формулы дифференцирования
1.  , в частности,
, в частности,  ;
;
2.  , в частности,
, в частности,  ;
;
3.  , в частности,
, в частности,  ;
;
4. 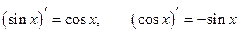 ;
;
5. 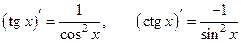 ;
;
6.  ;
;
7.  ;
;
8.  .
.
Производные высших порядков
Пусть 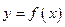 − дифференцируемая функция. Производная
− дифференцируемая функция. Производная 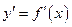 также является функцией от
также является функцией от  . Ее производная
. Ее производная 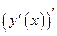 , если она существует, называется производной второго порядка и обозначается
, если она существует, называется производной второго порядка и обозначается  , или
, или  , или
, или  . Аналогично
. Аналогично  ,
,  ,… Производной
,… Производной 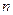 −го порядка функции называется производная от производной
−го порядка функции называется производная от производной  −го порядка:
−го порядка:
 .
.
Теоремы о среднем
Формула Тейлора
Во многих прикладных задачах требуется заменить сложную функцию  многочленом
многочленом  , близким к
, близким к  в окрестности точки
в окрестности точки  ,в том смысле, что
,в том смысле, что
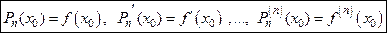 .
.
Введем ряд понятий.
1). Многочлен  , удовлетворяющий условию (9.3), называется многочленом Тейлора
, удовлетворяющий условию (9.3), называется многочленом Тейлора  −го порядка функции
−го порядка функции  в окрестности точки
в окрестности точки  .
.
2). Разность между функцией  и её многочленом Тейлора
и её многочленом Тейлора  обозначают
обозначают  :
: 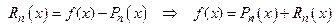 .
.
3). Формула  , где
, где  −многочлен Тейлора, называется формулой Тейлора n -го порядка для функции
−многочлен Тейлора, называется формулой Тейлора n -го порядка для функции  ,
,  называется остаточным членом формулы Тейлора.
называется остаточным членом формулы Тейлора.
Теорема 9.1 (о виде многочлена Тейлора).
Пусть функция  дифференцируема
дифференцируема 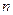 раз в окрестности точки
раз в окрестности точки  . Тогда многочлен Тейлора
. Тогда многочлен Тейлора 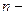 го порядка функции
го порядка функции  имеет вид:
имеет вид:
 .
.
Используя вид многочлена Тейлора, запишем формулу Тейлора 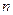 − го порядка:
− го порядка:
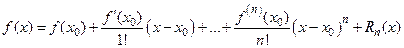 .
.
При  формула Тейлора называется формулой Маклорена и имеет вид:
формула Тейлора называется формулой Маклорена и имеет вид:
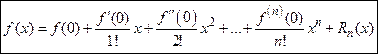
Рассмотрим вид остаточного члена  формулы Тейлора.
формулы Тейлора.
Теорема 9.2(об остаточном члене в форме Пеано).
Пусть функция  дифференцируема
дифференцируема 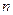 раз в окрестности точки
раз в окрестности точки  . Тогда остаточный член формулы Тейлора имеет вид:
. Тогда остаточный член формулы Тейлора имеет вид:
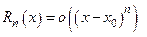 при
при  .
.
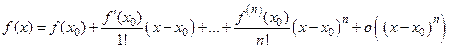 .
.
Эту формулу будем называть асимптотическим разложением  го порядка функции
го порядка функции 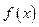 в окрестности точки
в окрестности точки  .
.
Теорема 9.3 (об остаточном члене в форме Лагранжа).
Пусть функция  дифференцируема
дифференцируема  раз в окрестности точки
раз в окрестности точки  . Тогда остаточный член формулы Тейлора в этой окрестности можно записать в форме
. Тогда остаточный член формулы Тейлора в этой окрестности можно записать в форме
 , (9.10)
, (9.10)
где 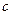 – некоторая точка между
– некоторая точка между  и
и  .
.
Асимптотические разложения
Элементарных функций
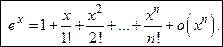
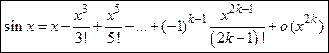 .
.
 .
.
 .
.
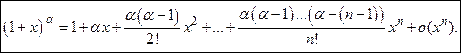

Монотонность функции
К монотонным функциям относятся функции, возрастающие или убывающие на промежутке. Напомним, что функция возрастает (соответственно убывает) на интервале  , если для любых точек
, если для любых точек  из этого интервала из неравенства
из этого интервала из неравенства 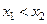 следует неравенство
следует неравенство  (соответственно
(соответственно 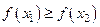 ).
).
Теорема 10.1 (критерий монотонности).
Дифференцируемая функция 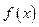 возрастает (соответственно убывает) на интервале
возрастает (соответственно убывает) на интервале  тогда и только тогда, когда
тогда и только тогда, когда  (соответственно
(соответственно  ) на интервале
) на интервале  .
.
Экстремумы функции
Пусть функция 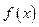 непрерывна на интервале
непрерывна на интервале  , содержащем точку
, содержащем точку  . Напомним ряд определений.
. Напомним ряд определений.
1). Точка  называется точкой максимум функции
называется точкой максимум функции 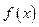 , если
, если  для всех
для всех  из некоторой выколотой окрестности точки
из некоторой выколотой окрестности точки  .
.
2). Точка  называется точкой минимума функции
называется точкой минимума функции 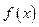 , если
, если  для всех
для всех  из некоторой выколотой окрестности точки
из некоторой выколотой окрестности точки  .
.
3). Точки максимума и минимума функции называют ее точками экстремума.
.
Теорема 10.2(необходимое условие экстремума).
Пусть функция 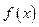 имеет экстремум в точке
имеет экстремум в точке  . Тогда производная
. Тогда производная  в точке
в точке  равна нулю или не существует.
равна нулю или не существует.
Точки экстремума, в которых 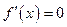 , назовем точками гладкого экстремума. В таких точках касательная к графику функции параллельна оси
, назовем точками гладкого экстремума. В таких точках касательная к графику функции параллельна оси 
1). Точки экстремума, в которых  не существует, назовем точками острого экстремума.
не существует, назовем точками острого экстремума.
2). Точки, в которых производная функции равна нулю или не существует, называют критическими точками функции
Для исследования критической точки на экстремум используют первое или второе достаточное условие экстремума.
Теорема 10.3 (первое достаточное условие экстремума).
Пусть функция 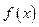 непрерывна в окрестности критической точки
непрерывна в окрестности критической точки  и дифференцируема в выколотой окрестности точки
и дифференцируема в выколотой окрестности точки  . Если производная
. Если производная  при переходе (слева направо) через точку
при переходе (слева направо) через точку  меняет знак с плюса на минус, то
меняет знак с плюса на минус, то  есть точка максимума; если с минуса на плюс, то
есть точка максимума; если с минуса на плюс, то  точка минимума.
точка минимума.
Теорема 10.4(второе достаточное условие экстремума).
Пусть 1)  2)
2)  .
.
Тогда, если  нечетное, то в точке
нечетное, то в точке  экстремума нет;
экстремума нет;
если 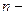 четное, то
четное, то  − точка экстремума, причем,
− точка экстремума, причем,
точка максимума при  , точка минимума при
, точка минимума при  .
.
Следствие. Пусть  .
.
Если  , то
, то  − точка максимума для
− точка максимума для 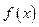 ;
;
если 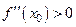 , то
, то  − точка минимума для
− точка минимума для 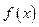 .
.
На отрезке
На практике часто встречаются задачи, в которых требуется найти наибольшее или наименьшее значение функции на отрезке. Напомним, что функция, непрерывная на отрезке, принимает на этом отрезке наибольшее и наименьшее значения. Эти значения она принимает либо в критических точках внутри отрезка, либо на концах отрезка. Поэтому для отыскания наибольшего и наименьшего значения непрерывной на отрезке  функции
функции 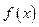 следует:
следует:
1) найти критические точки функции на интервале  ,
,
2) вычислить значения функции в этих критических точках (не исследуя их) и на концах отрезка,
3) из всех полученных значений функции выбрать наибольшее и наименьшее.
Асимптоты графика функции
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении этой точки по кривой от начала координат.
Таблица основных интегралов
1.  .
.
2.  .
.
3. 
4. 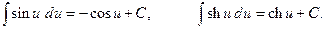 .
.
5.  .
.
6. 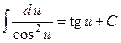 .
.
7.  .
.
8. 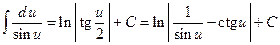 .
.
9. 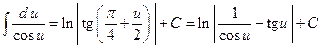 .
.
10. 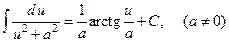 .
.
11.  .
.
12.  .
.
13. 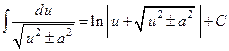 .
.
Метод замены переменной
Во многих случаях введение новой переменной интегрирования позволяет свести данный интеграл к более простому. Такой метод называется методом замены переменной или методом подстановки.
Пусть функция  непрерывно дифференцируема на промежутке и имеет обратную функцию
непрерывно дифференцируема на промежутке и имеет обратную функцию  . Тогда
. Тогда
 .
.
Выражение, стоящее в правой части этой формулы, означает, что после отыскания интеграла вместо  нужно подставить его выражение через
нужно подставить его выражение через  .
.
При замене переменной в интеграле 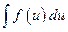 нужно
нужно
а) заменить переменную 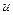 на функцию
на функцию 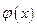 , заменить
, заменить  на
на  ,
,
б) вычислить получившийся интеграл,
в) результат выразить через первоначальную переменную 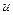 .
.
Укажем некоторые рекомендации по выбору новой переменной. Пусть 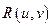 −рациональная функция, полученная из
−рациональная функция, полученная из  с помощью сложения, вычитания, умножения, деления. Приведем рекомендации по выбору новой переменной.
с помощью сложения, вычитания, умножения, деления. Приведем рекомендации по выбору новой переменной.
| Тип интеграла
| Замена
|

| 
|
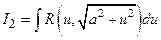
| 
|
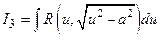
| 
|
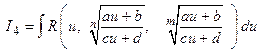
| 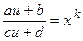 , ,
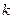 - наименьшее общее кратное чисел - наименьшее общее кратное чисел 
|
Случай 4.
 , где
, где  −рациональная функция от
−рациональная функция от 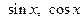 :
:
а) если  , то следует подынтегральное выражение выразить через
, то следует подынтегральное выражение выразить через  и
и  ,
,
б) в остальных случаях (не рассмотренных ранее) следует подынтегральное выражение выразить через  и
и  .
.
Предел и непрерывность функции одной переменной
Понятие предела является одним из важнейших понятий математического анализа. Основные понятия математического анализа, такие как производная, интеграл, связаны с предельным переходом.
Для сокращения записи мы будем использовать символы  − любой и
− любой и 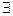 − существует. Запись
− существует. Запись  :
: 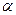 означает «для всякого элемента
означает «для всякого элемента  имеет место предложение
имеет место предложение 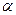 ». Запись
». Запись 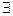
 :
: 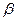 означает «существует элемент
означает «существует элемент  , для которого имеет место предложение
, для которого имеет место предложение 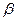 ». Запись
». Запись 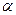

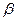 означает «из предложения
означает «из предложения 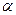 следует предложение
следует предложение 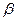 ». Запись
». Запись 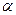

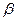 означает, что
означает, что 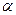 и
и 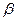 эквивалентны.
эквивалентны.
Для изучения пределов используется понятие окрестности точки.



 − любой и
− любой и 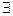 − существует. Запись
− существует. Запись  :
: 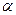 означает «для всякого элемента
означает «для всякого элемента  имеет место предложение
имеет место предложение  :
: 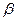 означает «существует элемент
означает «существует элемент 

 1).
1). 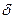 - окрестность конечной точки
- окрестность конечной точки  обозначим
обозначим  и определим как множество действительных чисел
и определим как множество действительных чисел 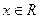 таких, что
таких, что  (рис.1):
(рис.1):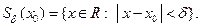
 2).
2).  и определим как множество действительных чисел
и определим как множество действительных чисел 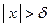 (рис.2). Итак,
(рис.2). Итак,
 .
.


 4).
4). 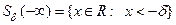 .
.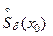 точки
точки  , которая получается из окрестности
, которая получается из окрестности  удалением точки
удалением точки 
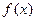 и предположим, что аргумент
и предположим, что аргумент  стремится к числу
стремится к числу 
 Если для всех
Если для всех 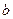 , то число
, то число  называют пределом функции
называют пределом функции  ; записывают это следующим образом:
; записывают это следующим образом: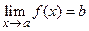 или
или  при
при 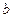 называется пределом функции
называется пределом функции 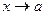 , если для любого положительного числа
, если для любого положительного числа  найдётся положительное число
найдётся положительное число  такое, что значения функции
такое, что значения функции  -окрестности точки
-окрестности точки 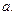
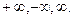 В дальнейшем это определение будем записывать кратко с помощью символов следующим образом:
В дальнейшем это определение будем записывать кратко с помощью символов следующим образом: если для
если для  такое, что
такое, что  для
для  3.2. Предел функции на языке неравенств
3.2. Предел функции на языке неравенств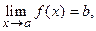
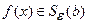 означает, что
означает, что  ;
; означает, что
означает, что 
 если для
если для 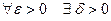 такое, что
такое, что
 , как только
, как только 
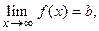
 означает, что
означает, что 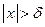
 если для
если для 

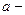 конечное число. Тогда
конечное число. Тогда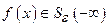 означает, что
означает, что  ,
,
 если для
если для  , как только
, как только 
 функции натурального аргумента
функции натурального аргумента 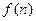 , расположенные в порядке возрастания аргумента
, расположенные в порядке возрастания аргумента …,
…,  …
…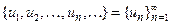 .
.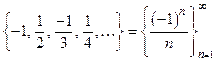 , 2)
, 2) 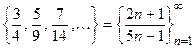 .
.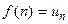 при
при 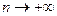 (обычно пишут
(обычно пишут  ), т.е.
), т.е. если для
если для 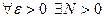 такое, что
такое, что  для
для 

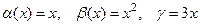 , являющихся бесконечно малыми при
, являющихся бесконечно малыми при 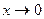 , имеем:
, имеем: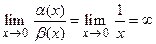 ,
, 
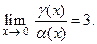
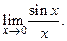 Он является неопределенностью
Он является неопределенностью 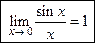 . (5.1)
. (5.1)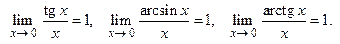
 и
и  − бесконечно малых при
− бесконечно малых при  стремится к нулю «быстрее», чем
стремится к нулю «быстрее», чем  и
и  бесконечно малые функции при
бесконечно малые функции при 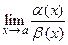 конечен и отличен от нуля, то
конечен и отличен от нуля, то 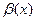 называют бесконечно малыми одного порядка и обозначают так:
называют бесконечно малыми одного порядка и обозначают так:  при
при  то
то  то
то 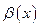 и обозначают так:
и обозначают так:  при
при  то
то 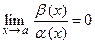 и
и  не существует, то
не существует, то 
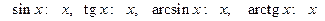 при
при 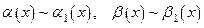 при
при 
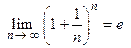 .
. 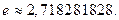
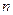 на действительное число
на действительное число  или на действительное число
или на действительное число  :
:
 понятие производной и ее применение, в частности, для исследования функций.
понятие производной и ее применение, в частности, для исследования функций. . Придадим аргументу
. Придадим аргументу  . Тогда функция
. Тогда функция  , которое характеризует изменение функции
, которое характеризует изменение функции 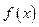 на отрезке
на отрезке 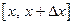 . Средняя скорость изменения функции на этом отрезке равна
. Средняя скорость изменения функции на этом отрезке равна  , а скорость изменения функции
, а скорость изменения функции 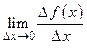 . Этот предел, если он существует, называется производной
. Этот предел, если он существует, называется производной  функции
функции 
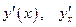 .
.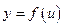 , а
, а 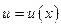 . Тогда
. Тогда 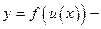 сложная функция с промежуточным аргументом
сложная функция с промежуточным аргументом 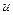 , независимым аргументом
, независимым аргументом 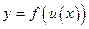 дифференцируема в точке
дифференцируема в точке  .
.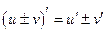 ,
, , в частности,
, в частности, 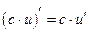 , где с − число,
, где с − число, , в частности,
, в частности, 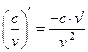 , где с − число,
, где с − число, , где
, где 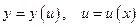 ,
,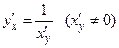 .
. , в частности,
, в частности,  ;
; , в частности,
, в частности,  ;
; , в частности,
, в частности,  ;
;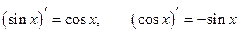 ;
;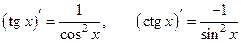 ;
; ;
; ;
; .
.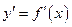 также является функцией от
также является функцией от 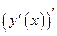 , если она существует, называется производной второго порядка и обозначается
, если она существует, называется производной второго порядка и обозначается  , или
, или  , или
, или  . Аналогично
. Аналогично  ,
,  ,… Производной
,… Производной  −го порядка:
−го порядка: .
. многочленом
многочленом  , близким к
, близким к  ,в том смысле, что
,в том смысле, что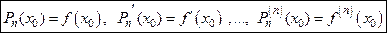 .
.  , удовлетворяющий условию (9.3), называется многочленом Тейлора
, удовлетворяющий условию (9.3), называется многочленом Тейлора  −го порядка функции
−го порядка функции  .
. :
: 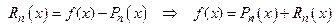 .
. , где
, где 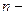 го порядка функции
го порядка функции  .
. 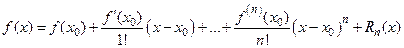 .
.  формула Тейлора называется формулой Маклорена и имеет вид:
формула Тейлора называется формулой Маклорена и имеет вид: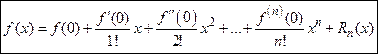
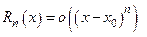 при
при  .
. 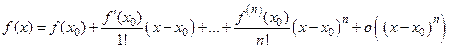 .
. го порядка функции
го порядка функции  раз в окрестности точки
раз в окрестности точки  , (9.10)
, (9.10)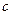 – некоторая точка между
– некоторая точка между 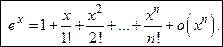
 .
.  .
.  .
. 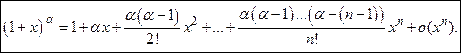

 , если для любых точек
, если для любых точек  из этого интервала из неравенства
из этого интервала из неравенства 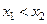 следует неравенство
следует неравенство  (соответственно
(соответственно 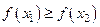 ).
). (соответственно
(соответственно  ) на интервале
) на интервале  для всех
для всех  для всех
для всех 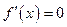 , назовем точками гладкого экстремума. В таких точках касательная к графику функции параллельна оси
, назовем точками гладкого экстремума. В таких точках касательная к графику функции параллельна оси 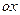
 точка минимума.
точка минимума. 2)
2)  .
. нечетное, то в точке
нечетное, то в точке  , точка минимума при
, точка минимума при  .
. .
. , то
, то 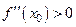 , то
, то  функции
функции  .
. .
.
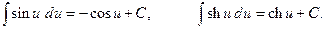 .
. .
.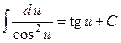 .
. .
.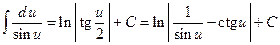 .
.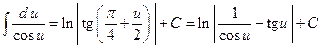 .
.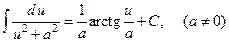 .
. .
. .
.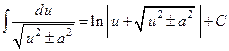 .
. непрерывно дифференцируема на промежутке и имеет обратную функцию
непрерывно дифференцируема на промежутке и имеет обратную функцию  . Тогда
. Тогда .
. 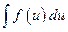 нужно
нужно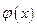 , заменить
, заменить  на
на  ,
,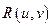 −рациональная функция, полученная из
−рациональная функция, полученная из  с помощью сложения, вычитания, умножения, деления. Приведем рекомендации по выбору новой переменной.
с помощью сложения, вычитания, умножения, деления. Приведем рекомендации по выбору новой переменной.

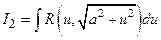

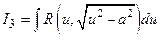

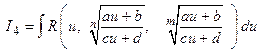
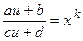 ,
,
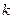 - наименьшее общее кратное чисел
- наименьшее общее кратное чисел 
 , где
, где  −рациональная функция от
−рациональная функция от 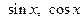 :
: , то следует подынтегральное выражение выразить через
, то следует подынтегральное выражение выразить через  и
и  ,
, и
и  .
.


