Пусть 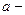 конечное число. В определении предела функции аргумент
конечное число. В определении предела функции аргумент  стремится к
стремится к  любым способом: колеблясь около
любым способом: колеблясь около  , оставаясь меньше
, оставаясь меньше  или больше
или больше  . Иногда важен способ приближения
. Иногда важен способ приближения  к
к  : слева
: слева  или справа
или справа  . Тогда вводят понятие левостороннего предела
. Тогда вводят понятие левостороннего предела 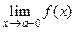 и правостороннего предела
и правостороннего предела 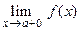 следующим образом:
следующим образом:
 если для
если для 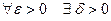 такое, что
такое, что 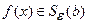 для
для 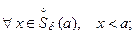
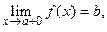 если для
если для 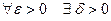 такое, что
такое, что 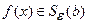 для
для 
Сформулируем очевидное утверждение:
Теоремы о функциях, имеющих конечный предел
Пусть 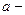 число или один из символов
число или один из символов 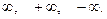
Теорема 4.1(о единственности предела).
Если существует конечный предел функции  при при  , то он единственен. , то он единственен.
|
Теорема 4.2.(об ограниченности функции, имеющей конечный предел).
Если функция имеет конечный предел при  , то она ограничена в некоторой выколотой окрестности точки
, то она ограничена в некоторой выколотой окрестности точки  .
.
Теорема 4.3 (о пределе монотонной ограниченной последовательности).
Если последовательность  возрастает и ограничена сверху, тоона имеет конечный предел при
возрастает и ограничена сверху, тоона имеет конечный предел при  .
.
Если последовательность  убывает и ограничена снизу, то она имеет конечный предел при
убывает и ограничена снизу, то она имеет конечный предел при  .
.
Теорема 4.4 (о сохранении неравенства).
Если 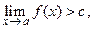 то
то  в некоторой выколотой окрестности точки
в некоторой выколотой окрестности точки 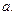
Если  то
то  в некоторой выколотой окрестности точки
в некоторой выколотой окрестности точки 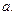
Теорема 4.5 (о предельном переходе в неравенстве).
Пусть существует 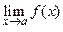 .
.
Если 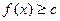 в некоторой выколотой окрестности точки
в некоторой выколотой окрестности точки  , то
, то 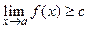 .
.
Если 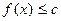 в некоторой выколотой окрестности точки
в некоторой выколотой окрестности точки  , то
, то 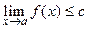 .
.
Теорема 4.6(о промежуточной функции). Пусть 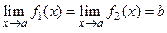 и и  в некоторой выколотой окрестности точки в некоторой выколотой окрестности точки 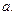 Тогда Тогда  . .
|
Теорема 4.7(о пределе суммы, произведения, частного).
Пусть существуют конечные пределы  и
и 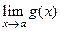 . Тогда
. Тогда
1) 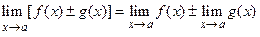 , 2)
, 2)  ,
,
3)  , 4)
, 4) 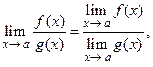 если
если  .
.
Теорема 4.8(о пределе сложной функции).
Пусть 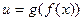 есть суперпозиция функций
есть суперпозиция функций 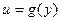 и
и 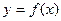 . Если существуют конечные пределы
. Если существуют конечные пределы 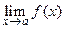 и
и  , то существует предел сложной функции
, то существует предел сложной функции  при
при  и
и 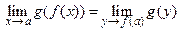 .
.
Для формулировки теоремы о пределе элементарной функции отметим, что элементарная функция получается из основных элементарных функций (степенной, показательной, логарифмической, тригонометрической, обратных тригонометрических) с помощью арифметических операций и суперпозиции.
Теорема 4.9 (о пределе элементарной функции). Пусть элементарная функция 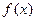 определена в точке определена в точке 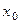 и ee окрестности. Тогда и ee окрестности. Тогда  . .
|
Бесконечно малые функции
Определение и основные свойства
Функция 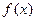 называется бесконечно малой при называется бесконечно малой при 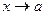 , если , если 
|
Рассмотрим ряд свойств бесконечно малых функций.
Теорема 5.1 (о связи функции с ее конечным пределом).
 ( (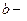 конечное) тогда и только тогда, когда конечное) тогда и только тогда, когда 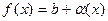 , где , где 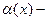 бесконечно малая функция при бесконечно малая функция при 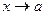 . .
|
Теорема 5.2(о произведении бесконечно малой функции на ограниченную).
Пусть функция  − бесконечно малая при
− бесконечно малая при 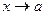 , а функция
, а функция 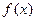 − ограничена в некоторой выколотой окрестности точки
− ограничена в некоторой выколотой окрестности точки  . Тогда произведение этих функций
. Тогда произведение этих функций  является бесконечно малой функцией при
является бесконечно малой функцией при 
Теорема 5.3(о сумме, разности, произведении бесконечно малых).
Сумма, разность, произведение конечного числа бесконечно малых функций при 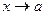 есть функция бесконечно малая при
есть функция бесконечно малая при 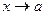 .
.
Отношение бесконечно малых.
Неопределенность 
В отличие от суммы и произведения, отношение бесконечно малых функций может иметь любой предел или даже его не иметь. Например, для функций 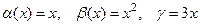 , являющихся бесконечно малыми при
, являющихся бесконечно малыми при 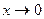 , имеем:
, имеем:
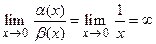 ,
, 
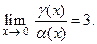
Поэтому отношение бесконечно малых функций называют неопределенностью вида  . Отыскание предела в случае неопределенности называют раскрытием неопределенности.
. Отыскание предела в случае неопределенности называют раскрытием неопределенности.
Первый замечательный предел
При вычислении пределов выражений, содержащих тригонометрические функции, часто используется 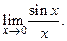 Он является неопределенностью
Он является неопределенностью  .
.
Покажем, что
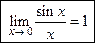 . (5.1)
. (5.1)
Это равенство называют первым замечательным пределом.
Следствие: 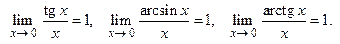
Сравнение бесконечно малых
Бесконечно малые функции часто сравнивают между собой по «быстроте» стремления к нулю. Так, например, из двух функций 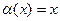 и
и  − бесконечно малых при
− бесконечно малых при 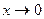 , функция
, функция 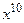 стремится к нулю «быстрее», чем
стремится к нулю «быстрее», чем  . Уточним, какой смысл вкладывается в слово «быстрее».
. Уточним, какой смысл вкладывается в слово «быстрее».
Пусть  и
и  бесконечно малые функции при
бесконечно малые функции при 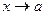 .
.
1). Если 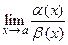 конечен и отличен от нуля, то
конечен и отличен от нуля, то  и
и 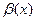 называют бесконечно малыми одного порядка и обозначают так:
называют бесконечно малыми одного порядка и обозначают так:  при
при  .
.
В частности, если  то
то  и
и 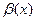 называют эквивалентными бесконечно малыми и обозначают так:
называют эквивалентными бесконечно малыми и обозначают так:  ~
~ 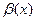 при
при  .
.
2). Если  то
то  называют бесконечно малой более высокого порядка, чем
называют бесконечно малой более высокого порядка, чем 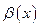 и обозначают так:
и обозначают так:  при
при  .
.
3). Если  то
то 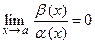 и
и 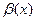 будет бесконечно малой более
будет бесконечно малой более
высокого порядка, чем  при
при  .
.
4). Если  не существует, то
не существует, то  и
и 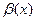 называют несравнимыми бесконечно малыми при
называют несравнимыми бесконечно малыми при  .
. 
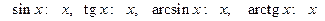 при при 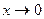 . .
|
Это вытекает из первого замечательного предела и его следствия.
Теорема 5.4 (об эквивалентных бесконечно малых).
Пусть 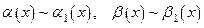 при при 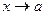 . Тогда . Тогда 
|
Бесконечно большие функции



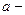 конечное число. В определении предела функции аргумент
конечное число. В определении предела функции аргумент  стремится к
стремится к  любым способом: колеблясь около
любым способом: колеблясь около  или справа
или справа  . Тогда вводят понятие левостороннего предела
. Тогда вводят понятие левостороннего предела 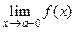 и правостороннего предела
и правостороннего предела 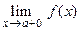 следующим образом:
следующим образом: если для
если для 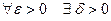 такое, что
такое, что 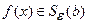 для
для 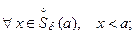
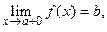 если для
если для 
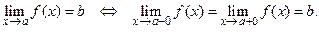
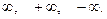
 при
при  , то он единственен.
, то он единственен.
 возрастает и ограничена сверху, тоона имеет конечный предел при
возрастает и ограничена сверху, тоона имеет конечный предел при  .
.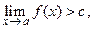 то
то  в некоторой выколотой окрестности точки
в некоторой выколотой окрестности точки 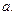
 то
то  в некоторой выколотой окрестности точки
в некоторой выколотой окрестности точки 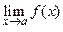 .
.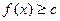 в некоторой выколотой окрестности точки
в некоторой выколотой окрестности точки 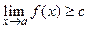 .
.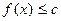 в некоторой выколотой окрестности точки
в некоторой выколотой окрестности точки 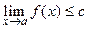 .
.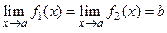 и
и  в некоторой выколотой окрестности точки
в некоторой выколотой окрестности точки  .
.
 и
и 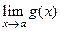 . Тогда
. Тогда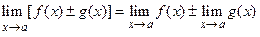 , 2)
, 2)  ,
, , 4)
, 4) 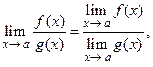 если
если  .
.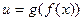 есть суперпозиция функций
есть суперпозиция функций 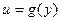 и
и 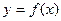 . Если существуют конечные пределы
. Если существуют конечные пределы 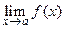 и
и  , то существует предел сложной функции
, то существует предел сложной функции  при
при 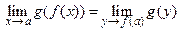 .
.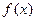 определена в точке
определена в точке 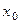 и ee окрестности. Тогда
и ee окрестности. Тогда  .
.
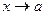 , если
, если 
 (
(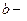 конечное) тогда и только тогда, когда
конечное) тогда и только тогда, когда 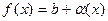 , где
, где 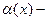 бесконечно малая функция при
бесконечно малая функция при  − бесконечно малая при
− бесконечно малая при  является бесконечно малой функцией при
является бесконечно малой функцией при 

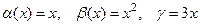 , являющихся бесконечно малыми при
, являющихся бесконечно малыми при 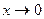 , имеем:
, имеем: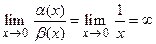 ,
, 
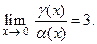
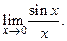 Он является неопределенностью
Он является неопределенностью 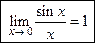 . (5.1)
. (5.1)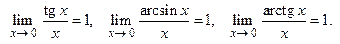
 и
и  − бесконечно малых при
− бесконечно малых при  стремится к нулю «быстрее», чем
стремится к нулю «быстрее», чем  бесконечно малые функции при
бесконечно малые функции при 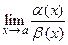 конечен и отличен от нуля, то
конечен и отличен от нуля, то 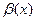 называют бесконечно малыми одного порядка и обозначают так:
называют бесконечно малыми одного порядка и обозначают так:  при
при  то
то  то
то 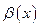 и обозначают так:
и обозначают так:  при
при  то
то 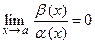 и
и  не существует, то
не существует, то 
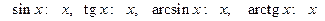 при
при  при
при 



