Методы последовательных приближений для

Решения нелинейных уравнений

 

6.1 Метод половинного деления

6.2 Метод хорд

6.3 Метод Ньютона (метод касательной)

6.4 Метод простых итераций

 

Метод половинного деления

 

При вычислении корня нелинейного уравнения методом половинного деления (метод ПД) решаемое уравнение должно быть приведено к виду

Y (Х)= 0                                        (7.1)

 

Графическая иллюстрация метода половинного деления приведена на рисунке 7.1.

 

 

Рисунок 7.1 – Графическая иллюстрация метода половинного

                   деления

Последовательность действий при решении уравнения методом ПД изложена ниже.

 

1) Задаются требуемой погрешностью вычислений ε _х по Х

Для большинства прикладных задач этот этап не вызывает затруднений, так как из физического смысла задачи и целей расчета достаточно ясно следуют требования к точности вычисления искомого параметра. Очевидно, что температуру в дымовой трубе котла нет смысла определять с точностью до сотых долей градуса. Весьма практично вначале задаться требуемой относительной точностью определения параметров, а затем перейти к абсолютным величинам погрешностей. Во многих расчетах относительная погрешность в 1-2 % вполне достаточна.

 

2) Задаются левой Х_л и правой Х_п границами интервала, на котором гарантированно находится решение. Решение на заданном отрезке должно быть только одно.

Для большинства прикладных задач и этот этап не вызывает затруднений, так как из физического смысла задачи достаточно очевидны минимальное и максимальное значение Х, которые могут наблюдаться в рассматриваемой ситуации. Например, температура некого тела, обменивающегося теплом конвекцией и излучением с другими телами, не может быть больше максимальной температуры окружающих тел, и меньше их минимальной температуры. В задаче, рассмотренной выше (рисунок 6.3), напор в точке Х не может быть больше отметки самого высоко расположенного бака, и не может быть меньше отметки самого низко расположенного бака.

Если все-таки поиск интервала вызывает затруднения, то задаются левой границей Х_л, вычисляют значение Y (Х_л), а затем с определенным шагом увеличивают Х, вычисляя каждый раз значение Y (Х), пока не изменит знак по отношению к Y (Х_л). Найденное значение Х принимается за правую границу, а предыдущее значение Х – за левую. Действуя таким образом, можно существенно сузить начальное значение интервала.

 

3) Вычисляют значение Y (Х_л) на левой границе интервала.

 

4) Вычисляют значение Х_ср в середине интервала

 

Х_ср = (Х_л + Х_п) / 2                                      (7.2)

 

5) Вычисляют значение Y (Х_ср) в середине интервала

 

6) Если Y (Х_ср) = 0, то Х_ср  есть решение, и расчет закончен. В противном случае расчет продолжается.

 

7) Определяют совпадение знаков функции на левой границе интервала Y (Х_л) и в середине Y (Х_ср) путем их перемножения (если знаки одинаковы, то произведение будет положительным, а если разные, то отрицательным).

В = Y (Х_л) × Y (Х_ср)                                         (7.3)

 

8) Если знак произведения В положителен, значит решение находится правее середины интервала, и левую границу следует переместить в середину, в противном случае в середину перемещается правая граница интервала.

если В>0, тогда Х_л = Х_ср , Y (Х_л) = Y (Х_ср)           (7.4)

 

если В <0, тогда Х_п = Х_ср                                    (7.5)

 

 Данное правило действует при любом наклоне линии функции Y (Х), как показано на рисунке 7.2

 

 

а) произведение В меньше 0

 

 

б) произведение В больше 0

 

 

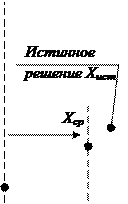Рисунок 7.1 – Иллюстрация правила сдвига границ интервала

9) Проверяют, не достигнута ли требуемая точность расчета. Если требуемая точность достигнута, то расчет прекращают, и за решение принимается середина интервала.

 

если (Х_п – Х_л)/2 ≤ ε _х, тогда Х = (Х_л + Х_п)/2                  (7.6)

 

10) Проводят следующий цикл вычислений, повторяя этапы расчета с пункта 4.

 

Таким образом, на каждом цикле расчета принятый ранее интервал сужается в два раза. После выполнения N итераций ширина интервала уменьшается в 2^N раз.

Метод ПД является достаточно медленным, так как на любом шаге следующее приближение может оказаться дальше от истинного решения, чем полученное на предыдущем шаге. Так, в примере на рисунке 7.1 значение середины отрезка на первом шаге X _ср1 значительно дальше отстоит от истинного решения, чем начальное приближение X _ср0, полученное делением исходного отрезка пополам.

Зато данный метод является очень простым и надежным, гарантирующим нахождение решения независимо от вида функции Y (Х). Сама функция может быть любой и иметь перегибы, максимумы и минимумы. Преимуществом этого МПП является так же то, что его реализация не требует вычисления производной от функции.

Программная реализация метода ПД очень проста, и составляет всего несколько строк на любом языке программирования.

 

Метод хорд

 

При вычислении корня нелинейного уравнения методом хорд решаемое уравнение также должно быть приведено к виду (7.1). Метод хорд дает хорошие результаты на плавных кривых, имеющих монотонный наклон. Его преимуществом является более быстрая сходимость, чем метода ПД. Объясняется это тем, что метод имеет монотонную сходимость – каждое последующее приближение находится ближе к истинному решению, чем предыдущее.

Как и для метода ПД, не требуется вычисление производной.

 

Графическая иллюстрация метода хорд приведена на рисунке 7.2.

 

 

Рисунок 7.2 – Графическая иллюстрация метода хорд

 

Последовательность действий при решении уравнения методом хорд изложена ниже.

 

1) Задаются требуемой погрешностью вычислений ε _х по Х

 

2) Задаются левой Х_л  и правой Х_п границами интервала, на котором гарантированно находится решение. Решение на заданном отрезке должно быть только одно.

 

3) Вычисляют значение Y (Х_п) на данном шаге решения на правой границе интервала.

 

4) Вычисляют значение Y (Х_л) на данном шаге решения на левой границе интервала.

 

5) Вычисляют значение X в точке пересечения хорды и оси абсцисс

Из построений на рисунке 7.2 можно записать пропорцию

(0 – Y _л) / (Y _п – Y _л) = (Х – Х_л) / (Х_п – Х_л)               (7.7)

 

Из (7.7) получим выражение для вычисления положения точки пересечения хорды и оси абсцисс

        

X = Х_л – Y _л /[(Х_п – Х_л)/(Y _п – Y _л)]                         (7.8)

или

X = Х_п – Y _п /[(Х_п – Х_л)/(Y _п – Y _л)]                         (7.9)

 

При этом выражение в квадратных скобках является тангенсом наклона хорды, соединяющей крайние точки функции.

 

6) Вычисляют значение Y (Х) на данном шаге решения в точке пересечения хорды и оси абсцисс.

 

7) Определяют совпадение знаков функции на левой границе интервала Y (Х_л) и в середине Y (Х) путем их перемножения (если знаки одинаковы, то произведение будет положительным, а если разные, то отрицательным).

В = Y (Х_л) × Y (Х)                                                   (7.10)

 

8) Если знак положителен, решение находится правее точки Х, и тогда левую границу следует переместить в точку Х, в противном случае в точку Х перемещается правая граница интервала.

 

если В>0, тогда Х_л = Х                  (7.11)

 

если В <0, тогда Х_п = Х                       (7.12)

 

9) Проверяют, не достигнута ли требуемая точность расчета. Если требуемая точность достигнута, то расчет прекращают, и за решение принимается середина интервала. Проверка точности является наиболее сложной задачей. Обычно оценивают разницу значений, полученных на предыдущем и текущем шаге

 

если   | (Х _i – Х _{i -1})| ≤ ε _х, тогда Х = Х _i              (7.13)

 

10) Проводят следующий цикл вычислений, повторяя этапы расчета с пункта 3.

 

Таким образом, на каждом цикле расчета принятый ранее интервал сужается. Метод хорд является достаточно быстрым, так как на любом шаге граница интервала неизбежно приближается к истинному решению – уход дальше просто невозможен.

Данный метод является очень простым и надежным, особенно он хорош для «гладких» функций, не имеющих перегибов. Достоинством этого МПП является так же то, что его реализация не требует вычисления производной от функции.

Программная реализация метода очень проста.