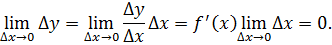Определение. Функция 𝑦 = 𝑓 (𝑥) называется непрерывной на отрезке [𝑎;𝑏], если она непрерывна в каждой точке интервала (𝑎; 𝑏), непрерывна справа в точке 𝑥=𝑎 и непрерывна слева в точке 𝑥=𝑏.
Теорема 9.1 (об устойчивости знака непрерывной функции). Пусть функция 𝑓(𝑥) непрерывна в точке 𝑎, и 𝑓(𝑎) 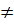 0. Тогда существует -окрестность точки 𝑎 такая, что в этой окрестности функция 𝑓(x) имеет тот же знак, что и 𝑓(𝑎).
0. Тогда существует -окрестность точки 𝑎 такая, что в этой окрестности функция 𝑓(x) имеет тот же знак, что и 𝑓(𝑎).
Доказательство. Пусть, например, 𝑓(𝑎)>0. Тогда по определению непрерывности 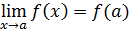 . Возьмем 𝜀=𝑓(𝑎). По определению предела для выбранного 𝜀 имеем
. Возьмем 𝜀=𝑓(𝑎). По определению предела для выбранного 𝜀 имеем
∃ 𝛿>0: ∀𝑥, 0<|𝑥−𝑎|<𝛿, |𝑓(𝑥)−𝑓(𝑎)|<𝜀=𝑓(𝑎).
Последнее неравенство можно переписать следующим образом:
−𝑓(𝑎)<𝑓(𝑥)−𝑓(𝑎)<𝑓(𝑎), 0<𝑓(𝑥)<2𝑓(𝑎).
Таким образом, ∀𝑥∈(𝑎−𝛿; 𝑎+𝛿) имеем неравенство 𝑓(𝑥)>0, доказывающее теорему.
Геометрический смысл теоремы об устойчивости знака состоит в том, что если функция 𝑓 непрерывна в точке 𝑎 и отлична в ней от нуля, то некоторая часть графика этой функции, проходящая через точку (𝑎; 𝑓(𝑎)), не пересекает ось 𝑂𝑥.
Теорема 9.2. (Больцано—Коши, первая). Пусть функция 𝑓(x) непрерывна на отрезке [𝑎, 𝑏] и на концах этого отрезка имеет значения разных знаков. Тогда существует точка 𝑐∈(𝑎; 𝑏), в которой 𝑓(𝑐)=0.
Доказательство. Отрезок [𝑎, 𝑏] разделим пополам. Если окажется, что в середине отрезка функция f (x) обращается в ноль, то теорема доказана. Если нет, то из двух отрезков выберем тот, у которого на концах отрезка функция f (x) имеет разные знаки и обозначим концы нового отрезка a 1 и b 1 . Продолжаем этот процесс. В результате возможны две ситуации. Первая – при очередном делении значение функции будет равно 0, тогда теорема доказана. Вторая – процесс бесконечен. Во втором случае получается система вложенных отрезков:
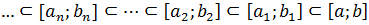 .
.
При этом 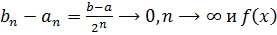 на концах отрезков имеет разные знаки. По теореме о стягивающихся отрезках существует единственная точка c, которая принадлежит всем отрезкам. Покажем, что f (c) =0. Предположим, что f (c)>0. Так как функция непрерывна в точке с, то по теореме 9.1 существует -окрестность точки с, в которой функция f (x) сохраняет знак значения f (c), то есть f (x)>0 при
на концах отрезков имеет разные знаки. По теореме о стягивающихся отрезках существует единственная точка c, которая принадлежит всем отрезкам. Покажем, что f (c) =0. Предположим, что f (c)>0. Так как функция непрерывна в точке с, то по теореме 9.1 существует -окрестность точки с, в которой функция f (x) сохраняет знак значения f (c), то есть f (x)>0 при 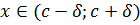 . Очевидно, что при достаточно большом n отрезок
. Очевидно, что при достаточно большом n отрезок 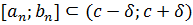 . Значит всюду в
. Значит всюду в 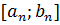 f (x)>0. Это противоречит тому, что на концах отрезка значения функции имеют разные знаки. Аналогично, если f (c)<0, то вновь получаем тоже противоречие. Этот факт и доказывает, что f (c)=0.
f (x)>0. Это противоречит тому, что на концах отрезка значения функции имеют разные знаки. Аналогично, если f (c)<0, то вновь получаем тоже противоречие. Этот факт и доказывает, что f (c)=0.
Геометрический смысл первой теоремы Больцано—Коши также очевиден. Поскольку функция 𝑓(x) непрерывна на отрезке, то ее график состоит из одного «сплошного» куска. Эта кривая соединяет точки (𝑎; 𝑓(𝑎)) и (𝑏; 𝑓(𝑏)), одна из которыетх лежит ниже оси 𝑂𝑥, вторая—выше оси 𝑂𝑥. Следовательно, существует точка 𝑐 на оси 𝑂𝑥, в которой график пересекает ось 𝑂𝑥.
Первую теорему Больцано—Коши легко обобщить.
Теорема 9.3 (Больцано—Коши, вторая). Пусть функция 𝑓(x) непрерывна на отрезке [𝑎; 𝑏], причем 𝑓(𝑎) 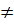 𝑓(𝑏), тогда, если 𝐶 —любое число, лежащее строго между 𝑓(𝑎) и 𝑓(𝑏), то существует точка 𝑐∈(𝑎; 𝑏) такая, что 𝑓(𝑐)=𝐶. Доказательство. Рассмотрим функцию g (x)= f (x)- C. Эта функция непрерывна на отрезке [𝑎; 𝑏] и на концах этого отрезка имеет значения с разными знаками. Следовательно, по теореме 9.2 существует точка 𝑐∈(𝑎; 𝑏) такая, что g (c)=0. Поэтому
𝑓(𝑏), тогда, если 𝐶 —любое число, лежащее строго между 𝑓(𝑎) и 𝑓(𝑏), то существует точка 𝑐∈(𝑎; 𝑏) такая, что 𝑓(𝑐)=𝐶. Доказательство. Рассмотрим функцию g (x)= f (x)- C. Эта функция непрерывна на отрезке [𝑎; 𝑏] и на концах этого отрезка имеет значения с разными знаками. Следовательно, по теореме 9.2 существует точка 𝑐∈(𝑎; 𝑏) такая, что g (c)=0. Поэтому 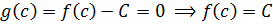 ч.т.д.
ч.т.д.
Иногда теорему 9.3 называют теоремой о промежуточном значении. Нетрудно понять и геометрический смысл второй теоремы Больцано—Коши.
Теорема 9.4 (Вейерштрасса, первая). Если функция 𝑓(x) непрерывна на отрезке [𝑎, 𝑏], то она ограничена на этом отрезке.
Доказательство. Докажем сначала, что функция 𝑓(x), непрерывная в заданной точке x0 ∈[𝑎; 𝑏], является ограниченной в некоторой окрестности этой точки. Действительно, из непрерывности следует, что 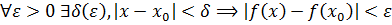 . Если в качестве
. Если в качестве 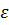 положить
положить  , то используя последнее неравенство, можно записать
, то используя последнее неравенство, можно записать 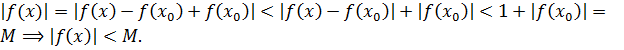 Следовательно, функция 𝑓(x) ограничена в интервале
Следовательно, функция 𝑓(x) ограничена в интервале 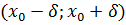 . Предположим теперь, что функция 𝑓(x) не ограничена на отрезке ∈[𝑎; 𝑏]. Разделим этот отрезок пополам и выберем тот, на котором заданная функция не ограничена. Обозначим новый отрезок так
. Предположим теперь, что функция 𝑓(x) не ограничена на отрезке ∈[𝑎; 𝑏]. Разделим этот отрезок пополам и выберем тот, на котором заданная функция не ограничена. Обозначим новый отрезок так 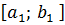 . Продолжая этот процесс, построим систему вложенных отрезков, длины которых стремятся к нулю. По теореме о стягивающихся отрезках существует единственная точка с, которая принадлежит всем построенным отрезкам. Очевидно, что при достаточно больших n отрезки
. Продолжая этот процесс, построим систему вложенных отрезков, длины которых стремятся к нулю. По теореме о стягивающихся отрезках существует единственная точка с, которая принадлежит всем построенным отрезкам. Очевидно, что при достаточно больших n отрезки 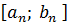 попадут в интервал
попадут в интервал 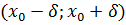 , но на этом интервале функция 𝑓(x) ограничена. Это противоречит условию неограниченности этой функции на отрезках
, но на этом интервале функция 𝑓(x) ограничена. Это противоречит условию неограниченности этой функции на отрезках 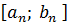 . Полученное противоречие и доказывает теорему.
. Полученное противоречие и доказывает теорему.
Заметим, что если в первой теореме Вейерштрасса вместо отрезка [𝑎; 𝑏] рассматривать интервал (𝑎; 𝑏) или какой-либо полуинтервал, то функция 𝑓(x) может оказаться и неограниченной. Например, функция 𝑓(𝑥)=1/𝑥 непрерывна на полуинтервале (0; 1], но не ограничена на нем.
Теорема 9.5 (Вейерштрасса, вторая). Непрерывная на отрезке [𝑎; 𝑏] функция 𝑓(x) достигает в некоторых точках этого отрезка своих точных верхней и нижней граней, т.е. существуют точки 𝛼 и 𝛽, принадлежащие [𝑎; 𝑏], для которых  .
.
Доказательство. Так как 𝑓(x) непрерывна на отрезке [𝑎; 𝑏], то она ограничена на этом отрезке по первой теореме Вейерштрасса. Отсюда следует, что множество значений функции 𝑓(x) ограничено и следовательно существует точная верхняя и точная нижняя грани этого множества. Пусть М - точная верхняя грань, тогда для любого x 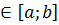 можно записать
можно записать 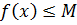 , где M не улучшаемая мажоранта. Предположим, что на рассматриваемом отрезке не найдется точки, в которой f (x) = М. Рассмотрим функцию F (x)=1/(M - f (x)). Она определена и положительна в любой точке отрезка
, где M не улучшаемая мажоранта. Предположим, что на рассматриваемом отрезке не найдется точки, в которой f (x) = М. Рассмотрим функцию F (x)=1/(M - f (x)). Она определена и положительна в любой точке отрезка 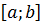 и является непрерывной на этом отрезке. Тогда по теореме 9.4 эта функция ограничена:
и является непрерывной на этом отрезке. Тогда по теореме 9.4 эта функция ограничена: 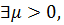 что
что 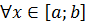 F (x)<
F (x)< 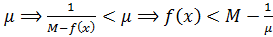 , но это неравенство противоречит тому, что М не улучшаемая мажоранта. Полученное противоречие доказывает, что в
, но это неравенство противоречит тому, что М не улучшаемая мажоранта. Полученное противоречие доказывает, что в 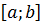 найдется точка
найдется точка 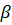 , в которой f (
, в которой f ( 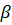 )= M. Аналогично можно показать, что найдется точка
)= M. Аналогично можно показать, что найдется точка 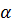 из
из 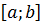 такая, что f (
такая, что f ( 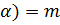 , где m – точная нижняя грань.
, где m – точная нижняя грань.
Замечание 9.2. Из этой теоремы вытекает, что для непрерывной на отрезке функции точную верхнюю грань можно назвать максимальным значением функции f (x), а точную нижнюю грань – минимальным значением той же функции на рассматриваемом отрезке.
Замечание 9.3. Разность между наибольшим и наименьшим значениями функции f (x) на отрезке 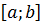 называется колебанием непрерывной функции на этом отрезке и обозначается буквой
называется колебанием непрерывной функции на этом отрезке и обозначается буквой 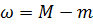 .
.
Пусть функция f (x) определена на множестве Х.
Определение. Функция f (x) называется равномерно непрерывной на множестве Х, если для любого 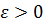 существует такое
существует такое 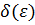 , зависящее только от
, зависящее только от 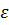 , что из неравенства
, что из неравенства 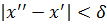 следует неравенство
следует неравенство 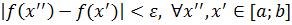 .
.
Из приведенного определения вытекает, что если функция равномерно непрерывна, то она и просто непрерывна, но не наоборот. Основное отличие непрерывной функции от равномерно непрерывной в том, что если функция просто непрерывна и не является равномерно непрерывной, то невозможно подобрать числа 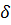 подходящее для всех элементов множества Х.
подходящее для всех элементов множества Х.
Теорема 9.6. (Теорема Кантора). Если функция f (x) непрерывна на отрезке 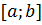 , то она и равномерно непрерывная на этом отрезке.
, то она и равномерно непрерывная на этом отрезке.
Доказательство. Сначала докажем, что если функция непрерывна на отрезке 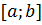 , то для любого
, то для любого 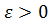 можно разбить этот отрезок на конечное число отрезков, любые два из которых или не имеют общих точек, или имеют одну общую граничную точку и на каждом из них для любых точек
можно разбить этот отрезок на конечное число отрезков, любые два из которых или не имеют общих точек, или имеют одну общую граничную точку и на каждом из них для любых точек 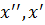 будет выполняться неравенство
будет выполняться неравенство 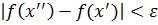 .
.
Предположим противное, то есть существует число 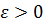 , при котором нельзя осуществить такое разбиение. Разделим тогда рассматриваемый отрезок пополам и выберем тот, который тоже нельзя разбить. Обозначим его
, при котором нельзя осуществить такое разбиение. Разделим тогда рассматриваемый отрезок пополам и выберем тот, который тоже нельзя разбить. Обозначим его 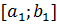 и т.д. Продолжая этот процесс неограниченно получаем систему вложенных отрезков, длины которых стремятся к нулю. По теореме о стягивающихся отрезках существует единственная точка с, которая принадлежит всем отрезкам. Так как функция f (x) непрерывна в точке с, то для любого
и т.д. Продолжая этот процесс неограниченно получаем систему вложенных отрезков, длины которых стремятся к нулю. По теореме о стягивающихся отрезках существует единственная точка с, которая принадлежит всем отрезкам. Так как функция f (x) непрерывна в точке с, то для любого 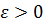 существует такое
существует такое 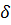 , что для любого х из
, что для любого х из 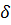 - окрестности точки с будет выполняться неравенство
- окрестности точки с будет выполняться неравенство 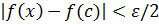 . Если взять
. Если взять 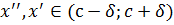 , то можно записать
, то можно записать 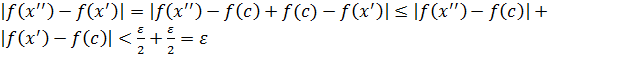 , то есть
, то есть 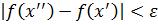 .
.
В 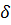 - окрестность точки с попадает отрезок
- окрестность точки с попадает отрезок 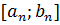 при достаточно большом n, но этот отрезок характеризуется тем, что для его точек последнее неравенство не выполняется. Получили противоречие, которое доказывает возможность соответствующего разбиения.
при достаточно большом n, но этот отрезок характеризуется тем, что для его точек последнее неравенство не выполняется. Получили противоречие, которое доказывает возможность соответствующего разбиения.
Итак, пусть 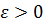 выбрано произвольно. Разобьем отрезок
выбрано произвольно. Разобьем отрезок 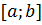 на конечное число частей так, чтобы любые два отрезка или не имеют общих точек, или имеют одну граничную общую точку и на каждом из отрезков выполняется неравенство
на конечное число частей так, чтобы любые два отрезка или не имеют общих точек, или имеют одну граничную общую точку и на каждом из отрезков выполняется неравенство 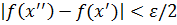 для любых
для любых 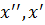 . Длину наименьшего отрезка примем за
. Длину наименьшего отрезка примем за 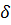 . Произвольно выберем точки
. Произвольно выберем точки 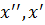 такие, что
такие, что 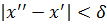 при этом возможны два случая 1)
при этом возможны два случая 1) 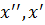 попали в один и тот же отрезок, а тогда
попали в один и тот же отрезок, а тогда 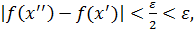 2)
2) 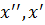 попали в соседние отрезки. Пусть
попали в соседние отрезки. Пусть 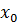 – граничная точка и в данном случае можем записать
– граничная точка и в данном случае можем записать  . Таким образом, по заданному
. Таким образом, по заданному 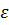 указано
указано 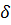 , не зависящее от
, не зависящее от 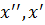 и такое, что из неравенства
и такое, что из неравенства 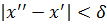 следует соотношение
следует соотношение 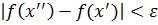 ч.т.д.
ч.т.д.
Лекция 10.
Понятие производной
Пусть функция 𝑦=𝑓(𝑥) определена и непрерывна в окрестности точки 𝑥=𝑎. Если независимой переменной 𝑥 придать приращение Δ𝑥 в этой точке, то функция получит соответствующее приращение Δ𝑦=𝑓(𝑎+Δ𝑥)−𝑓(𝑎). По определению непрерывной функции, если Δ𝑥→0, то и Δ𝑦→0.
Если же мы хотим получить представление, как быстро изменяется значение функции при изменении независимой переменной в окрестности точки 𝑥=𝑎, то должны сопоставить или сравнить каким то образом приращение аргумента Δ𝑥 и приращение функции Δ𝑦. С целью более глубокого изучения функции, исследования скорости изменения ее значений вводится понятие производной — одно из важнейших понятий математики.
Определение. Производной функции 𝑦=𝑓(𝑥) в точке 𝑥=𝑎 называется предел отношения приращения функции в этой точке к приращению аргумента, когда приращение аргумента стремится к нулю.
Для обозначения производной используются символы: 𝑓′(𝑎), 𝑦′(𝑎), 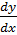 . Таким образом, по определению
. Таким образом, по определению
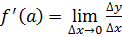 , где Δ𝑦=𝑓(𝑎+Δ𝑥)−𝑓(𝑎).
, где Δ𝑦=𝑓(𝑎+Δ𝑥)−𝑓(𝑎).
Определение. Операцию нахождения производной называют дифференцированием.
Если функция 𝑦=𝑓(𝑥) имеет производную 𝑓′(𝑥) в каждой точке 𝑥 ∈ 𝑋, то производную можно рассматривать как функцию переменной 𝑥 на 𝑋.
Из определения производной следует и способ ее вычисления.
Пример 10.1. Найти производную функции 𝑓(𝑥) = 𝑥2 + 2𝑥 + 2 в точке 𝑥=𝑎, 𝑎 ∈ R.
Решение. Придадим приращение Δ𝑥 аргументу в точке 𝑥=𝑎. Найдем соответствующее приращение Δ𝑦 функции 𝑦=𝑓(𝑥):
Δ𝑦=𝑓(𝑎+Δ𝑥)−𝑓(𝑎)=((𝑎+Δ𝑥)2+2(𝑎+Δ𝑥)+2)−(𝑎2+2𝑎+2)=2𝑎Δ𝑥+(Δ𝑥)2+2Δ𝑥=
=(2𝑎+2+Δ𝑥)Δ𝑥.
Теперь воспользуемся определением производной: 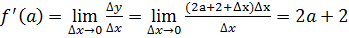
Таким образом, 𝑓′(𝑎)=2(𝑎+1), 𝑎 ∈ R.
Пример 10.2. Найти производную функции 𝑓(𝑥)=|𝑥−1| в точке 𝑥=1.
Решение. Исходя из определения производной, рассмотрим предел
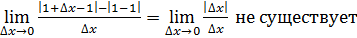 , так как
, так как 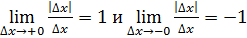 .
.
Видно, что в этом случае существуют односторонние пределы неравные между собой. Таким образом, производная функции 𝑓(𝑥)=|𝑥−1| в точке 𝑥=1 не существует.
Выясним связь между существованием производной в точке и непрерывностью функции.
Теорема 10.1. Если функция 𝑦=𝑓(𝑥) в точке 𝑥 имеет производную 𝑓′(𝑥), то она непрерывна в этой точке.
Доказательство. Действительно, обозначим Δ𝑦=𝑓(𝑥+Δ𝑥)−𝑓(𝑥). Будем иметь
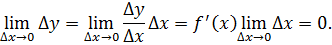
Это означает, что функция 𝑦=𝑓(𝑥) непрерывна в точке 𝑥.
Обратное утверждение неверно. Функция может быть непрерывной в точке, но не иметь в ней производной. Это видно на примере 10.2. Функция 𝑦=|𝑥−1| в точке 𝑥=1 непрерывна, но не имеет в ней производной.



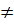 0. Тогда существует -окрестность точки 𝑎 такая, что в этой окрестности функция 𝑓(x) имеет тот же знак, что и 𝑓(𝑎).
0. Тогда существует -окрестность точки 𝑎 такая, что в этой окрестности функция 𝑓(x) имеет тот же знак, что и 𝑓(𝑎).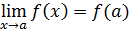 . Возьмем 𝜀=𝑓(𝑎). По определению предела для выбранного 𝜀 имеем
. Возьмем 𝜀=𝑓(𝑎). По определению предела для выбранного 𝜀 имеем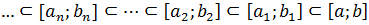 .
.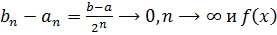 на концах отрезков имеет разные знаки. По теореме о стягивающихся отрезках существует единственная точка c, которая принадлежит всем отрезкам. Покажем, что f (c) =0. Предположим, что f (c)>0. Так как функция непрерывна в точке с, то по теореме 9.1 существует -окрестность точки с, в которой функция f (x) сохраняет знак значения f (c), то есть f (x)>0 при
на концах отрезков имеет разные знаки. По теореме о стягивающихся отрезках существует единственная точка c, которая принадлежит всем отрезкам. Покажем, что f (c) =0. Предположим, что f (c)>0. Так как функция непрерывна в точке с, то по теореме 9.1 существует -окрестность точки с, в которой функция f (x) сохраняет знак значения f (c), то есть f (x)>0 при 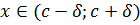 . Очевидно, что при достаточно большом n отрезок
. Очевидно, что при достаточно большом n отрезок 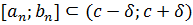 . Значит всюду в
. Значит всюду в 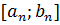 f (x)>0. Это противоречит тому, что на концах отрезка значения функции имеют разные знаки. Аналогично, если f (c)<0, то вновь получаем тоже противоречие. Этот факт и доказывает, что f (c)=0.
f (x)>0. Это противоречит тому, что на концах отрезка значения функции имеют разные знаки. Аналогично, если f (c)<0, то вновь получаем тоже противоречие. Этот факт и доказывает, что f (c)=0.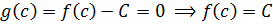 ч.т.д.
ч.т.д.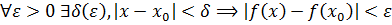 . Если в качестве
. Если в качестве 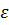 положить
положить  , то используя последнее неравенство, можно записать
, то используя последнее неравенство, можно записать 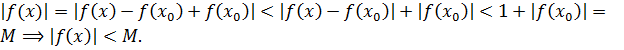 Следовательно, функция 𝑓(x) ограничена в интервале
Следовательно, функция 𝑓(x) ограничена в интервале 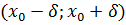 . Предположим теперь, что функция 𝑓(x) не ограничена на отрезке ∈[𝑎; 𝑏]. Разделим этот отрезок пополам и выберем тот, на котором заданная функция не ограничена. Обозначим новый отрезок так
. Предположим теперь, что функция 𝑓(x) не ограничена на отрезке ∈[𝑎; 𝑏]. Разделим этот отрезок пополам и выберем тот, на котором заданная функция не ограничена. Обозначим новый отрезок так 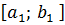 . Продолжая этот процесс, построим систему вложенных отрезков, длины которых стремятся к нулю. По теореме о стягивающихся отрезках существует единственная точка с, которая принадлежит всем построенным отрезкам. Очевидно, что при достаточно больших n отрезки
. Продолжая этот процесс, построим систему вложенных отрезков, длины которых стремятся к нулю. По теореме о стягивающихся отрезках существует единственная точка с, которая принадлежит всем построенным отрезкам. Очевидно, что при достаточно больших n отрезки 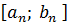 попадут в интервал
попадут в интервал  .
.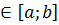 можно записать
можно записать 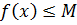 , где M не улучшаемая мажоранта. Предположим, что на рассматриваемом отрезке не найдется точки, в которой f (x) = М. Рассмотрим функцию F (x)=1/(M - f (x)). Она определена и положительна в любой точке отрезка
, где M не улучшаемая мажоранта. Предположим, что на рассматриваемом отрезке не найдется точки, в которой f (x) = М. Рассмотрим функцию F (x)=1/(M - f (x)). Она определена и положительна в любой точке отрезка 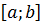 и является непрерывной на этом отрезке. Тогда по теореме 9.4 эта функция ограничена:
и является непрерывной на этом отрезке. Тогда по теореме 9.4 эта функция ограничена: 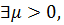 что
что 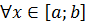 F (x)<
F (x)< 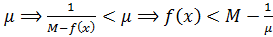 , но это неравенство противоречит тому, что М не улучшаемая мажоранта. Полученное противоречие доказывает, что в
, но это неравенство противоречит тому, что М не улучшаемая мажоранта. Полученное противоречие доказывает, что в 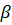 , в которой f (
, в которой f ( 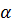 из
из 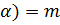 , где m – точная нижняя грань.
, где m – точная нижняя грань.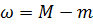 .
.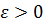 существует такое
существует такое 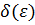 , зависящее только от
, зависящее только от 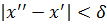 следует неравенство
следует неравенство 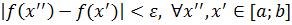 .
.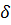 подходящее для всех элементов множества Х.
подходящее для всех элементов множества Х.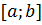 , то она и равномерно непрерывная на этом отрезке.
, то она и равномерно непрерывная на этом отрезке.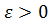 можно разбить этот отрезок на конечное число отрезков, любые два из которых или не имеют общих точек, или имеют одну общую граничную точку и на каждом из них для любых точек
можно разбить этот отрезок на конечное число отрезков, любые два из которых или не имеют общих точек, или имеют одну общую граничную точку и на каждом из них для любых точек 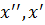 будет выполняться неравенство
будет выполняться неравенство 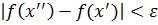 .
.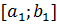 и т.д. Продолжая этот процесс неограниченно получаем систему вложенных отрезков, длины которых стремятся к нулю. По теореме о стягивающихся отрезках существует единственная точка с, которая принадлежит всем отрезкам. Так как функция f (x) непрерывна в точке с, то для любого
и т.д. Продолжая этот процесс неограниченно получаем систему вложенных отрезков, длины которых стремятся к нулю. По теореме о стягивающихся отрезках существует единственная точка с, которая принадлежит всем отрезкам. Так как функция f (x) непрерывна в точке с, то для любого 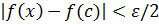 . Если взять
. Если взять 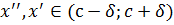 , то можно записать
, то можно записать 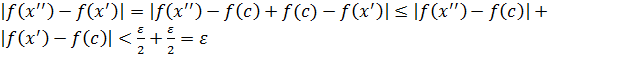 , то есть
, то есть 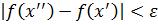 .
.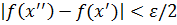 для любых
для любых 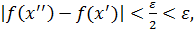 2)
2) 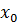 – граничная точка и в данном случае можем записать
– граничная точка и в данном случае можем записать  . Таким образом, по заданному
. Таким образом, по заданному 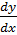 . Таким образом, по определению
. Таким образом, по определению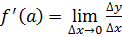 , где Δ𝑦=𝑓(𝑎+Δ𝑥)−𝑓(𝑎).
, где Δ𝑦=𝑓(𝑎+Δ𝑥)−𝑓(𝑎).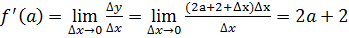
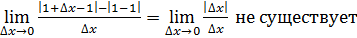 , так как
, так как 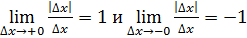 .
.