1. Свойства операции сложения.
1) x+y=y+x, 
2) x+(y+z)=(y+x)+z, 
3) x +0= x, 
4) x +(- x)=0, 
Свойства операции умножения.
1) x 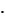 y=y
y=y 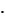 x,
x, 
2) x 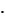 (y
(y 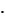 z) =(y
z) =(y  x)
x)  z,
z, 
3) x  1= x,
1= x, 
4) x 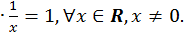
Связь сложения и умножения.
1) 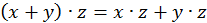
Операции порядка.
1) 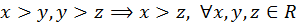
2) 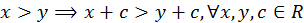
Архимедово свойство действительных чисел.
Для любого действительного числа  существует натуральное число n такое, что n > a.
существует натуральное число n такое, что n > a.
Действительно, для любого  можно взять
можно взять 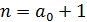 .
.
Свойство непрерывности.
Определение 2.1. Множество 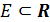 называется ограниченным сверху (снизу), если существует число
называется ограниченным сверху (снизу), если существует число 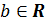 , такое что
, такое что 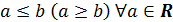 , при этом число
, при этом число 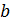 называют мажорантой (минорантой) множества
называют мажорантой (минорантой) множества 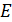 .
.
Определение 2.2. Множество ограниченное сверху и снизу называется ограниченным.
Определение 2.3. Наименьшая мажоранта ограниченного сверху множества Е называется точной верхней гранью Е и обозначается символом supE.
Число с= supE если выполняются два условия:
1. с – мажоранта Е
2. Любое число d < c уже не является мажорантой.
Аналогично, точная нижняя грань Е это наибольшая миноранта ограниченного снизу множества Е, которая обозначается так infE.
Число с= infE если выполняются два условия:
3. с – миноранта Е
4. Любое число d > c уже не является минорантой.
Свойство непрерывности. Непустое ограниченное сверху (снизу) множество действительных чисел имеет точную верхнюю (точную нижнюю) грань.
Доказательство. Покажем сначала справедливость этого утверждения для для множеств с положительными элементами. Пусть M такое множество. Так как M ограничено сверху, то существует число r такое, что 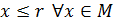 . Очевидно, что среди всех чисел r найдутся целые. Пусть
. Очевидно, что среди всех чисел r найдутся целые. Пусть 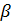 наименьшее целое, являющееся мажорантой. Таким образом, число
наименьшее целое, являющееся мажорантой. Таким образом, число 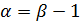 уже не будет мажорантой. Рассмотрим интервал
уже не будет мажорантой. Рассмотрим интервал 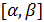 и разделим его на 10 равных частей. Получим:
и разделим его на 10 равных частей. Получим: 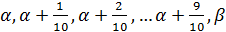 . Ясно, что перебирая эти числа можно подобрать пару чисел:
. Ясно, что перебирая эти числа можно подобрать пару чисел: 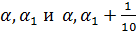 , которые удовлетворяют свойству:
, которые удовлетворяют свойству:  – мажоранта. Полученный интервал опять разделим на 10 равных частей и проделаем аналогичную процедуру. В результате получаем новый интервал и
– мажоранта. Полученный интервал опять разделим на 10 равных частей и проделаем аналогичную процедуру. В результате получаем новый интервал и  –мажоранта. Продолжая этот процесс, на n-шаге получаем:
–мажоранта. Продолжая этот процесс, на n-шаге получаем: 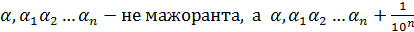 – мажоранта. В общем случае, продолжая указанный процесс, получаем бесконечную десятичную дробь
– мажоранта. В общем случае, продолжая указанный процесс, получаем бесконечную десятичную дробь 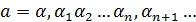 , которая и будет точной верхней гранью. Действительно, если на каком-то шаге
, которая и будет точной верхней гранью. Действительно, если на каком-то шаге 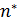 число
число 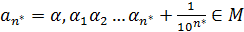 , то это будет наибольшим числом в М и поэтому для любого
, то это будет наибольшим числом в М и поэтому для любого 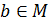 имеем
имеем 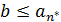 и в этом случае можно положить
и в этом случае можно положить 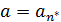 . Пусть теперь c любая мажоранта из
. Пусть теперь c любая мажоранта из 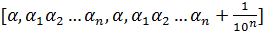 . Тогда
. Тогда 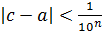 для любых
для любых 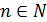 . Следовательно, можно считать с=а и а – мажоранта. Если взять число d < a, то найдется такое n, при котором
. Следовательно, можно считать с=а и а – мажоранта. Если взять число d < a, то найдется такое n, при котором 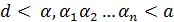 , но
, но 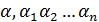 не мажоранта и, следовательно, d тем более не может быть мажорантой. Поэтому а является точной верхней гранью.
не мажоранта и, следовательно, d тем более не может быть мажорантой. Поэтому а является точной верхней гранью.
Пусть теперь М произвольное множество ограниченное сверху. В этом случае возникает два случая
1). Множество М содержит хотя бы один положительный элемент. В этом случае обозначим 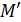 множество положительных элементом из M. Очевидно, что это множество ограничено сверху и поэтому имеет точную верхнюю грань, которая и является точной верхней гранью заданного множества.
множество положительных элементом из M. Очевидно, что это множество ограничено сверху и поэтому имеет точную верхнюю грань, которая и является точной верхней гранью заданного множества.
2). Множество М не содержит ни одного положительного элемента. Пусть 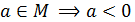 . Добавим ко всем элементам множества М величину –а+1. Полученное множество обозначим
. Добавим ко всем элементам множества М величину –а+1. Полученное множество обозначим 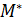 . Это множество ограничено сверху и имеет единственный положительный элемент 1, а значит, мы приходим к случаю 1). Следовательно, и в этом случае существует точная верхняя грань.
. Это множество ограничено сверху и имеет единственный положительный элемент 1, а значит, мы приходим к случаю 1). Следовательно, и в этом случае существует точная верхняя грань.
Для точной нижней грани справедливы аналогичные рассуждения. В результате убеждаемся, что если множество М ограничено снизу, то оно имеет точную нижнюю грань.
С амостоятельно. Принцип разделяющего чис ла. Теорема о стягивающихся отрезках. (Мордкович А.Г.)
Пример. Доказать, что множество X = 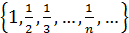 ограничено и найти точную верхнюю и точную нижнюю грани.
ограничено и найти точную верхнюю и точную нижнюю грани.
Решение. При любом натуральном n справедливо неравенство 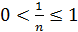 . Значит множество ограничено сверху и снизу, а значит ограничено. Мажорантой множества Х является число 1. Это число является и точной верхней гранью, так как если взять любое меньшее число c, то 1> c и с не является мажорантой. Точной нижней гранью является 0, так как 0 – миноранта и для любого большего числа c найдется n такое, что 1/ n < c и с не может быть минорантой.
. Значит множество ограничено сверху и снизу, а значит ограничено. Мажорантой множества Х является число 1. Это число является и точной верхней гранью, так как если взять любое меньшее число c, то 1> c и с не является мажорантой. Точной нижней гранью является 0, так как 0 – миноранта и для любого большего числа c найдется n такое, что 1/ n < c и с не может быть минорантой.
Числовые множества иногда удобно изображать множествами точек на прямой, которая в этом случае называется числовой прямой. Для этого на прямой выбирается точка, которая принимается за нулевой элемент. Все точки справа от О будем считать изображают положительные числа, а слева – отрицательные. Затем выбирается отрезок, принимаемый за 1. Откладываем этот отрезок на оси вправо от О, получаем точку 1. Затем можно изобразить все целые числа. Точки прямой, лежащие между точками, изображающими целые числа, соответствуют рациональным и иррациональным числам.






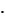 y=y
y=y 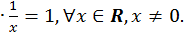
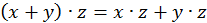
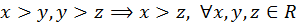
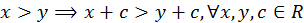
 существует натуральное число n такое, что n > a.
существует натуральное число n такое, что n > a. можно взять
можно взять 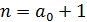 .
.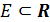 называется ограниченным сверху (снизу), если существует число
называется ограниченным сверху (снизу), если существует число 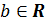 , такое что
, такое что 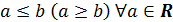 , при этом число
, при этом число 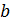 называют мажорантой (минорантой) множества
называют мажорантой (минорантой) множества 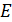 .
.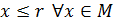 . Очевидно, что среди всех чисел r найдутся целые. Пусть
. Очевидно, что среди всех чисел r найдутся целые. Пусть 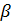 наименьшее целое, являющееся мажорантой. Таким образом, число
наименьшее целое, являющееся мажорантой. Таким образом, число 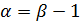 уже не будет мажорантой. Рассмотрим интервал
уже не будет мажорантой. Рассмотрим интервал 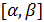 и разделим его на 10 равных частей. Получим:
и разделим его на 10 равных частей. Получим: 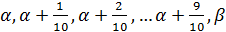 . Ясно, что перебирая эти числа можно подобрать пару чисел:
. Ясно, что перебирая эти числа можно подобрать пару чисел: 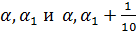 , которые удовлетворяют свойству:
, которые удовлетворяют свойству:  – мажоранта. Полученный интервал опять разделим на 10 равных частей и проделаем аналогичную процедуру. В результате получаем новый интервал и
– мажоранта. Полученный интервал опять разделим на 10 равных частей и проделаем аналогичную процедуру. В результате получаем новый интервал и  –мажоранта. Продолжая этот процесс, на n-шаге получаем:
–мажоранта. Продолжая этот процесс, на n-шаге получаем: 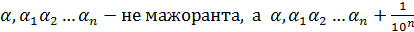 – мажоранта. В общем случае, продолжая указанный процесс, получаем бесконечную десятичную дробь
– мажоранта. В общем случае, продолжая указанный процесс, получаем бесконечную десятичную дробь 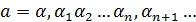 , которая и будет точной верхней гранью. Действительно, если на каком-то шаге
, которая и будет точной верхней гранью. Действительно, если на каком-то шаге 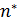 число
число 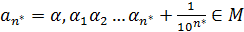 , то это будет наибольшим числом в М и поэтому для любого
, то это будет наибольшим числом в М и поэтому для любого 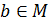 имеем
имеем 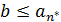 и в этом случае можно положить
и в этом случае можно положить 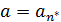 . Пусть теперь c любая мажоранта из
. Пусть теперь c любая мажоранта из 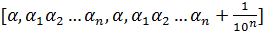 . Тогда
. Тогда 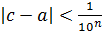 для любых
для любых 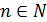 . Следовательно, можно считать с=а и а – мажоранта. Если взять число d < a, то найдется такое n, при котором
. Следовательно, можно считать с=а и а – мажоранта. Если взять число d < a, то найдется такое n, при котором 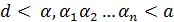 , но
, но 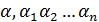 не мажоранта и, следовательно, d тем более не может быть мажорантой. Поэтому а является точной верхней гранью.
не мажоранта и, следовательно, d тем более не может быть мажорантой. Поэтому а является точной верхней гранью.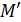 множество положительных элементом из M. Очевидно, что это множество ограничено сверху и поэтому имеет точную верхнюю грань, которая и является точной верхней гранью заданного множества.
множество положительных элементом из M. Очевидно, что это множество ограничено сверху и поэтому имеет точную верхнюю грань, которая и является точной верхней гранью заданного множества.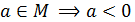 . Добавим ко всем элементам множества М величину –а+1. Полученное множество обозначим
. Добавим ко всем элементам множества М величину –а+1. Полученное множество обозначим 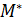 . Это множество ограничено сверху и имеет единственный положительный элемент 1, а значит, мы приходим к случаю 1). Следовательно, и в этом случае существует точная верхняя грань.
. Это множество ограничено сверху и имеет единственный положительный элемент 1, а значит, мы приходим к случаю 1). Следовательно, и в этом случае существует точная верхняя грань.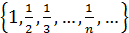 ограничено и найти точную верхнюю и точную нижнюю грани.
ограничено и найти точную верхнюю и точную нижнюю грани.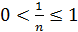 . Значит множество ограничено сверху и снизу, а значит ограничено. Мажорантой множества Х является число 1. Это число является и точной верхней гранью, так как если взять любое меньшее число c, то 1> c и с не является мажорантой. Точной нижней гранью является 0, так как 0 – миноранта и для любого большего числа c найдется n такое, что 1/ n < c и с не может быть минорантой.
. Значит множество ограничено сверху и снизу, а значит ограничено. Мажорантой множества Х является число 1. Это число является и точной верхней гранью, так как если взять любое меньшее число c, то 1> c и с не является мажорантой. Точной нижней гранью является 0, так как 0 – миноранта и для любого большего числа c найдется n такое, что 1/ n < c и с не может быть минорантой.


