Числовые множества и их свойства.

Введение.

Математический анализ – это совокупность разделов математики, посвященных исследованию функций и их обобщений методами дифференциального и интегрального исчисления. По праву можно считать, что математический анализ является фундаментом математических знаний. Основные его положения были сформулированы к концу XVII века. Основоположниками математического анализа следует считать Исаак Ньютона и Готфрида Лейбница.

Исаак Ньютон (1642 - 1727 гг.) – выдающийся английский ученый. Биография Ньютонабогата во всех смыслах этого слова. Он сделал немало открытий в области физики, астрономии, механике и математике.

Готфрид Вильгельм Лейбниц (1646 — 1716 гг.) — саксонский философ, логик, математик, механик, физик, юрист, историк, дипломат, изобретатель и языковед. Основатель и первый президент Берлинской Академии наук, иностранный член Французской Академии наук. Он один из первых описал двоичную систему счислений.

В дальнейшем существенный вклад в развитие математического анализа внесли такие выдающиеся ученые, как Огюст Коши (Огюстен Луи Коши (1789-1857гг) - выдающийся французский математик), Карл Вейерштрасс (Карл Теодор Вильгельм Вейерштрасс (1815 —1897 гг.) — немецкий математик), Бернхард Риман (Георг Фридрих Бе́рнхард Ри́ман (1826-1866 гг,) — немецкий математик, механик и физик.) и многие другие. Среди Российских математиков следует выделить Леонарда Эйлера (1707 – 1783гг.), Николая Ивановича Лобачевского (1792 – 1856гг.), Михаила Васильевича Остроградского (1801-1862гг.).

 

                              Элементы теории множеств                

Понятие множества или совокупности принадлежит к числу простейших математических понятий. Оно не имеет точного определения. Однако это понятие широко используется в математике, поэтому мы должны договориться о том, что будем понимать под словом множество. Общепринято считать, что множество это совокупность или набор некоторых объектов, предметов, при этом каждый такой объект называется элементом множества. Основатель теории множеств Георг Кантор (1845-1918гг.) выразил это следующими словами: «Множество есть многое, мыслимое, как единое». Таким образом, любое множество задается своими элементами.

Примерами являются множество книг в библиотеке или множество студентов, присутствующих на занятии. Обычно множество обозначают заглавными латинскими буквами (A), а его элементы строчными латинскими буквами (a). То, что элемент принадлежит множеству, обозначают так: aÎA. Если a не принадлежит A, то этот факт обозначают так: aÏA. Чтобы задать множество, следует или перечислить его элементы, или указать характеристическое свойство его элементов, то есть такое свойство, которым обладают все элементы множества и только они. Например, множество планет, вращающихся вокруг солнца.

Множества могут содержать как конечное число элементов, так и бесконечное много элементов. Если множество не содержит ни одного элемента, то такое множество называется пустым и обозначается специальным символом Æ.

Два множества равны тогда и только тогда, когда состоят из одних и тех же элементов. Если все элементы множества A содержатся в множестве B, то говорят, что A является подмножеством множества B и обозначают AÌB. Поэтому A = B означает, что A Ì B и одновременно B Ì A.

 

Операции над множествами.

Основными операциями над множествами являются следующие:

1. Дополнение. Пусть дано множество U. Тогда для любого множества A Ì U определим дополнение: A^с ={ b Î U | b Ï A }.

2. Объединение. Для любых двух множеств A, B Ì U определим объединение: A È B ={ c Î U | (c Î A) или (c Î B)}. Например, A ={ a, b, c, d } и B ={ c, d, e }, тогда A È B ={ a, b, c, d, e }.

3. Пересечение. Для любых двух множеств A, B Ì U определим пересечение: A Ç B ={ c Î U | (c Î A) и одновременно (c Î B)}.

Например, A ={ a, b, c, d } и B ={ c, d, e }, тогда A Ç B ={ c, d }.

Для иллюстрации операций над множествами вводят диаграммы Эйлера-Венна – круги, обозначающие множества. Так, введенные нами операции иллюстрируются следующим образом.

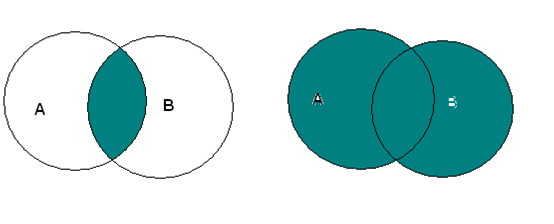
A Ç B                                            A È B

Кроме введенных нами трех операций над множествами существуют

еще операции, которые могут быть представлены как комбинация

простейших операций. Введем операцию вычитания множеств:

A \ B ={ c Î U | (c Î A) и одновременно (c Ï B)}. На диаграмме Эйлера-Венна

результат вычитания выглядит так:

 

 

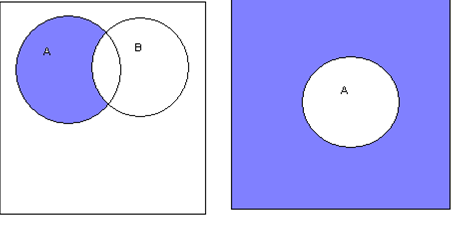
А \ В                                      B ^c = U\ В

Можно доказать, что A/B = A Ç B ^c. Для доказательства равенства двух множеств следует убедиться в том, что все элементы первого множества принадлежат второму и все элементы второго множества принадлежат первому.

Помимо введенных операций над множествами рассматривают декартово произведение двух множеств. Декартовым произведением множеств A и B называется множество A ´ B, элементы которого задаются двумя элементами, из которых первый – элемент множества A, а второй – элемент множества B.

Например, если A – множество названий всех улиц какого-то города, B – множество номеров домов от 1-го до 10-го, то A ´ B – множество адресов городских домов, расположенных в начале улиц. В данном случае количество этих адресов равно произведению количеству городских улиц на 10.

Лекция 2.

Связь сложения и умножения.

1)

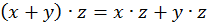
Операции порядка.

1)

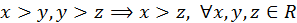
2)

 

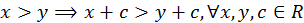
Свойство непрерывности.

Определение 2.1. Множество 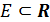  называется ограниченным сверху (снизу), если существует число 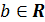, такое что 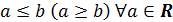, при этом число  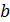называют мажорантой (минорантой) множества .

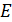Определение 2.2. Множество ограниченное сверху и снизу называется ограниченным.

Определение 2.3. Наименьшая мажоранта ограниченного сверху множества Е называется точной верхней гранью Е и обозначается символом supE.

Число с= supE если выполняются два условия:

1. с – мажоранта Е

2. Любое число d < c уже не является мажорантой.

Аналогично, точная нижняя грань Е это наибольшая миноранта ограниченного снизу множества Е, которая обозначается так infE.

Число с= infE если выполняются два условия:

3. с – миноранта Е

4. Любое число d > c уже не является минорантой.

Свойство непрерывности. Непустое ограниченное сверху (снизу) множество действительных чисел имеет точную верхнюю (точную нижнюю) грань.

Доказательство. Покажем сначала справедливость этого утверждения для для множеств с положительными элементами. Пусть M такое множество. Так как M ограничено сверху, то существует число r такое, что 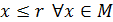. Очевидно, что среди всех чисел r найдутся целые. Пусть  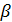наименьшее целое, являющееся мажорантой. Таким образом, число  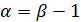уже не будет мажорантой. Рассмотрим интервал  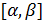и разделим его на 10 равных частей. Получим: 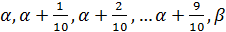. Ясно, что перебирая эти числа можно подобрать пару чисел: 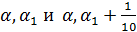, которые удовлетворяют свойству:  – мажоранта. Полученный интервал опять разделим на 10 равных частей и проделаем аналогичную процедуру. В результате получаем новый интервал и  –мажоранта. Продолжая этот процесс, на n-шаге получаем: 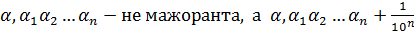 – мажоранта. В общем случае, продолжая указанный процесс, получаем бесконечную десятичную дробь 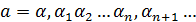, которая и будет точной верхней гранью. Действительно, если на каком-то шаге  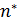число 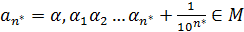, то это будет наибольшим числом в М и поэтому для любого  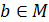имеем 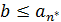 и в этом случае можно положить 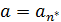. Пусть теперь c любая мажоранта из 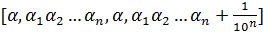. Тогда  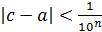для любых 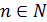. Следовательно, можно считать с=а и а – мажоранта. Если взять число d < a, то найдется такое n, при котором 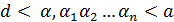, но 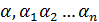 не мажоранта и, следовательно, d тем более не может быть мажорантой. Поэтому а является точной верхней гранью.

Пусть теперь М произвольное множество ограниченное сверху. В этом случае возникает два случая

1). Множество М содержит хотя бы один положительный элемент. В этом случае обозначим 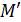 множество положительных элементом из M. Очевидно, что это множество ограничено сверху и поэтому имеет точную верхнюю грань, которая и является точной верхней гранью заданного множества.

2). Множество М не содержит ни одного положительного элемента. Пусть 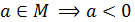. Добавим ко всем элементам множества М величину –а+1. Полученное множество обозначим 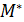. Это множество ограничено сверху и имеет единственный положительный элемент 1, а значит, мы приходим к случаю 1). Следовательно, и в этом случае существует точная верхняя грань.

Для точной нижней грани справедливы аналогичные рассуждения. В результате убеждаемся, что если множество М ограничено снизу, то оно имеет точную нижнюю грань.

С амостоятельно. Принцип разделяющего чис ла. Теорема о стягивающихся отрезках. (Мордкович А.Г.)

Пример. Доказать, что множество X = 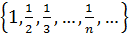 ограничено и найти точную верхнюю и точную нижнюю грани.

Решение. При любом натуральном n справедливо неравенство 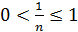. Значит множество ограничено сверху и снизу, а значит ограничено. Мажорантой множества Х является число 1. Это число является и точной верхней гранью, так как если взять любое меньшее число c, то 1> c и с не является мажорантой. Точной нижней гранью является 0, так как 0 – миноранта и для любого большего числа c найдется n такое, что 1/ n < c и с не может быть минорантой.

Числовые множества иногда удобно изображать множествами точек на прямой, которая в этом случае называется числовой прямой. Для этого на прямой выбирается точка, которая принимается за нулевой элемент. Все точки справа от О будем считать изображают положительные числа, а слева – отрицательные. Затем выбирается отрезок, принимаемый за 1. Откладываем этот отрезок на оси вправо от О, получаем точку 1. Затем можно изобразить все целые числа. Точки прямой, лежащие между точками, изображающими целые числа, соответствуют рациональным и иррациональным числам.

Предел последовательности

Изучение предела последовательности — основного понятия этого параграфа, начнем с наводящего примера. Рассмотрим последовательность 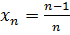; или 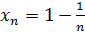. Из последнего выражения видно, что с увеличением n числа  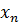приближаются к значению a =1. Действительно, оценим степень близости элемента  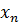к 1: 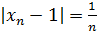 и с увеличением n расстояние между элементами последовательности и числом 1 неограниченно сокращается. В таком случае говорят, что число 1 является пределом последовательности { }.

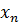Получив, на конкретном примере, представление о сути предельного перехода, мы готовы перейти к математически строгому определению предела.

Определение. Число 𝑎 называется пределом последовательности { 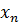}, если для всякого числа 𝜀 > 0, сколь малым оно бы ни было, существует номер 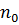∈ N такой, что для всех 𝑛 >  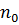имеет место неравенство | 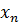−𝑎|<𝜀. На языке кванторов это выглядит так: ∀ 𝜀 > 0 ∃  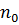∈ N: ∀ 𝑛 >  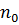| 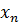−𝑎|<𝜀.

Для обозначения предела используется выражение .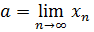

Пример. Пусть дана последовательность . Доказать, что пределом последовательности является число a =1/2, используя определение предела.

Решение. Рассмотрим величину 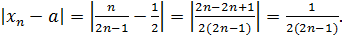 Возьмем произвольное 𝜀 > 0 и запишем неравенство 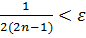. Решая это неравенство, находим 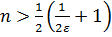. Обозначим 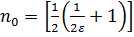+1, тогда при  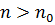будет выполняться неравенство  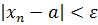ч.т.д.

Если последовательность имеет конечный предел, то говорят, что она сходится. В противном случае – расходится.

Бесконечно малые последовательности.

Если последовательность сходится и ее предел равен 0, то она называется бесконечно малой. Пользуясь определением предела, можно дать определение бесконечно малой последовательности на языке 𝜀.

Определение. Последовательность 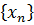 называется бесконечно малой если ∀ 𝜀 > 0 ∃  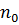∈ N: ∀ 𝑛 >  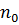| |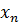<𝜀.

Свойства бесконечно малых последовательностей (БМП):

1. Сумма конечного числа бесконечно малых последовательностей есть БМП. [Доказательство]

2. Бесконечно малая последовательность является ограниченной. [Доказательство]

3. Произведение бесконечно малой последовательности и ограниченной последовательности есть БМП. [Доказательство]

4. Произведение нескольких БМП есть БМП. [Доказательство]

5. Если БМП { 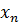} имеет постоянное значение 𝑎, т.е. ∀ 𝑛 ∈ N верно, что 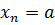, то 𝑎 = 0. [Доказательство]

Бесконечно большие последовательности (ББП).

Определение. Последовательность 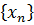 называется бесконечно большой, если для любого числа А>0, каким бы большим оно ни было, найдется такой номер 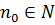, что при  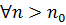выполняется неравенство 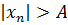. При этом пишут .

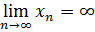Если окажется, что при любом А>0 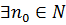 такой, что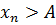 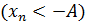 при 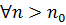, то пишут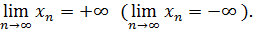

Свойства бесконечно больших последовательностей.

1. ББП—неограниченная последовательность.

2. Произведение двух ББП есть ББП.

3. Сумма ББП и ограниченной последовательности есть ББП.

4. ББП не может являться постоянной последовательностью.

Замечание. Сумма двух ББП не обязательно является ББП. Например, последовательност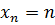и  и 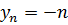 бесконечно большие. Однако, сумма 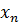+ 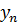=0 бесконечно большой не является.

Последовательности БМП и ББП связаны между собой. На это указывает следующая теорема.

ТЕОРЕМА 3.1. Если { 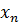} есть ББП и все ее члены отличны от нуля, то последовательность {1/ 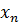} есть БМП; и обратно, если { 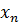}—БМП, все члены которой отличны от нуля, то {1/ 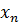}—ББП.

Доказательство. Пусть { 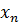} есть ББП. Это значит, что для любого A >0 в том числе и для A =1/𝜀  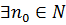такой, что при  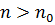выполняется неравенство 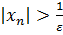. Из этого неравенства сразу следует, что  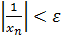ч.т.д. Обратное утверждение доказывается аналогично.

Лекция 4.

Лекция 5.

Функции.

Понятие функции

При изучении явлений природы, физических, экономических и других процессов часто встречаются с совокупностью переменных величин, которые связаны между собой так, что значения одних величин полностью определяют значения других. Например, площадь круга 𝑆 однозначно определяется значением его радиуса с помощью формулы .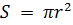

Определение. Пусть 𝑋 и 𝑌 — два произвольных множества. Если каждому элементу 𝑥 из множества 𝑋 по некоторому правилу 𝑓 поставлен в соответствие единственный элемент 𝑦 из множества 𝑌, то говорят, что задана функция 𝑓. Функцию 𝑓, как правило, обозначают одним из следующих способов: 𝑦=𝑓(𝑥), 𝑓: 𝑋→𝑌.

Переменная 𝑥 называется независимой переменной, или аргументом функции, переменная 𝑦 — зависимой переменной, или значением функции. Множество 𝑋 называют областью определения, или областью существования функции 𝑓 и обозначают 𝐷(𝑓). Множество всех значений, принимаемых функцией 𝑓, когда аргумент 𝑥 пробегает всю область определения 𝑋, называется множеством значений функции 𝑓, обозначается 𝐸(𝑓):

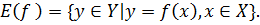
Множество значений функции 𝐸(𝑓) содержится, очевидно, в 𝑌. При этом 𝑌 может также содержать элементы, не входящие в 𝐸(𝑓).

Определение. Если 𝑋⊂R и 𝑌⊂R, то есть 𝑋 и 𝑌 являются числовыми множествами, то функция 𝑓: 𝑋→𝑌 называется числовой. Например, функция 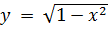 определена на отрезке [−1; 1], т.е. областью определения является множество 𝑋=[−1; 1]. Множеством значений функции в данном случае является отрезок [0; 1], 𝑌=[0; 1].

Определение. Функция, все значения которой равны между собой, называется постоянной. Постоянную функцию часто обозначают буквой 𝐶.

Определение. Графиком функции называется множество всех точек плоскости с координатами (𝑥; 𝑓(𝑥)), т.е. координаты 𝑥 и 𝑦 точек графика связаны соотношением 𝑦=𝑓(𝑥).

Например, графиком функции 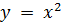 является парабола. Естественно, что графиком функции не обязательно является «сплошная» кривая. В частности, графиком функции 𝑦 = 𝑛! будет бесконечное множество изолированных точек.

Пример 5.1. Найти 𝑓(2), 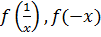, если 𝑓(𝑥)=1+𝑥+𝑥².

Решение. Очевидно, 𝑓(2)=1+2+2²=7. Если вместо независимого переменного подставить выражение 1/ x, то получим:

.

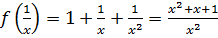Аналогично, 𝑓(−𝑥)=1+(−𝑥)+(−𝑥)²=1−𝑥+𝑥².

Пример 5.2. Определить область определения функции 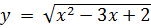. Данная функция существует, если подкоренное выражение больше нуля или равно нулю, то есть 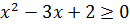. Решая это неравенство, находим множество допустимых значений для х: .

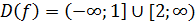5.2. Способы задания функции.

Чтобы задать функцию, требуется указать правило: как по каждому значению аргумента 𝑥 находить соответствующее значение функции 𝑦=𝑓(𝑥). Существуют три основных способа задания функции: аналитический, табличный и графический.

1. Аналитический способ. Если зависимость между переменными выражена с помощью формул, то говорят, что функция задана аналитически. Формула, задающая функцию, указывает совокупность действий, которые нужно в определенном порядке произвести, чтобы получить соответствующее значение функции.

Рассмотрим, например, выражение 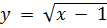. Функция, заданная этой формулой, определена на промежутке [1;+∞). Чтобы вычислить значение функции ∀𝑥∈[1;+∞), необходимо от значения аргумента 𝑥 вычесть 1 и извлечь из полученного числа квадратный корень. Множеством значений является промежуток [0;+∞). Графиком функции является множество всех точек плоскости с координатами (𝑥; 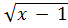). Переменная 𝑥 пробегает здесь промежуток [1,+∞) (рисунок 5.1).

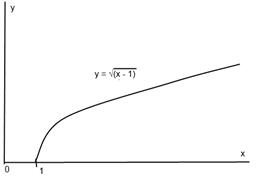
Рис.5.1. График функции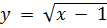

Рассмотрим выражение вида:

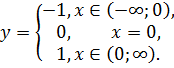
В этом примере функция задана тремя формулами. Эту функцию обозначают так: .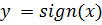

2. Табличный способ. Предположим, что нас интересует зависимость расхода топлива от скорости движения легкового автомобиля определенной марки. В инструкции к автомобилю имеется таблица 5.1. Из таблицы видно, что расход топлива изменяется в зависимости от скорости движения автомобиля и,  если  каждому значению скорости, записанному в первой строке таблицы,

 

Таблица 5.1

Скорость движения (км/час)	70	80	90	100	110	120
Расход топлива (л/100 км)	6.6	6.3	6.1	6.4	7.0	8.0

 

поставить в соответствие число литров топлива, стоящих во второй строке и в этом столбце, то получим функцию, заданную таблично.

Областью определения этой функции является множество из 6 чисел, стоящих в первой строке. Множеством значений является также совокупность из 6 чисел второй строки. С помощью таблицы часто задают функции, значения которых вычислить сложно. Например, широко известны таблицы тригонометрических функций, показательной и логарифмической функций и т.д. Заметим, что имеются способы перехода от функций, заданных таблично, к функциям, которые заданы аналитически. Безусловно, это можно сделать, как правило, лишь приближенно.

3. Графический способ. В данном случае предполагается, что задан график функции 𝑦=𝑓(𝑥). Тогда, чтобы для некоторого значения аргумента 𝑥 найти соответствующее значение функции, нужно построить на оси 𝑂𝑥 точку 𝑥, затем восстановить в этой точке перпендикуляр к оси 𝑂𝑥, найти точку пересечения этого перпендикуляра с графиком и найти длину этого перпендикуляра. Значение функции будет равно этому числу с соответствующим знаком.

Примерами графического изображения могут быть записи самопишущих приборов (барографы, осциллографы и т.д.).

Элементарные функции

Значительную роль в математике и ее приложениях играет небольшой набор функций, которые принято называть основными элементарными функциями. Перечислим их.

1. Простейшей является постоянная функция 𝑦 = 𝐶.

2. Степенная функция имеет вид 𝑦 = 𝑥^𝛼, где 𝛼 ∈ R. Примеры степенных функций с различными показателями: .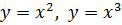

Первая функция означает, что для того чтобы получить y нужно x умножить на x. Область определения у этой функции - 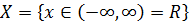, а область значений - 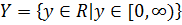. Функция четная и, следовательно, ее график симметричен относительно оси OY. В области [0;  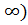заданная функция строго монотонна (строго монотонно возрастает), то есть 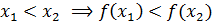, так как . Это значит, рассматриваемая функция имеет обратную 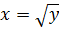. Таким образом, определена операция возведение в степень ½ или взятие квадратного корня. Если рассмотреть функцию 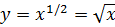, то ее график будет зеркальным отражением функции  относительно биссектрисы угла первой четверти, при этом функция 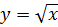 будет также строго монотонной.

Аналогичные рассуждения можно провести и для функции 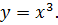 При этом устанавливается существование функции 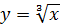, которая является обратной к заданной.

В общем случае можно говорить о степенной функции, у которой 𝛼=m/n – рациональное число. Если 𝛼 – иррациональное число, то его можно представить, как предел последовательности рациональных чисел и определить 𝑥^𝛼 = 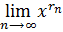, где .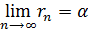

2. Показательная функция .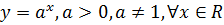

3. Обратная к показательной – логарифмическая функция, которая записывается так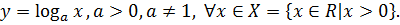

4. Тригонометрические функции 𝑦 = sin 𝑥 (синус), 𝑦 = cos 𝑥 (косинус), 𝑦 = tg𝑥 (тангенс) и 𝑦 = ctg𝑥 (котангенс) являются периодическими.

5. Обратные тригонометрические функции 𝑦 = arcsin𝑥 (арксинус), 𝑦 = arccos𝑥 (арккосинус), 𝑦 = arctg𝑥 (арктангенс) и 𝑦 = arcctg𝑥 (арккотангенс).

Определение. Функция, составленная из основных элементарных функций с помощью операций сложения, вычитания, умножения, деления и суперпозиции, называется элементарной функцией.

Определение. Простейшими элементарными функциями являются целая рациональная функция, или алгебраический многочлен

𝑃(𝑥) = 𝑎₀𝑥^𝑛 + 𝑎₁𝑥^𝑛−1 + 𝑎₂𝑥^𝑛−2 +... + 𝑎_𝑛−2𝑥² + 𝑎_𝑛−1𝑥 + 𝑎_𝑛, 𝑛 ∈ N,

а также дробная рациональная функция

𝑅(𝑥) = 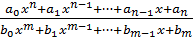, 𝑛, m ∈ N

Множество целых и дробных рациональных функций образует класс рациональных функций.

Определение. Функции, не являющиеся элементарными, называются неэлементарными.

В качестве характерных примеров отметим неэлементарные функции 𝑦 = |𝑥| и 𝑦 = sign 𝑥.

В данном курсе мы сосредоточим внимание преимущественно на элементарных функциях.

Лекция 6.

Предел Функции.

6.1. Предел функции по Гейне.

  Определение. Пусть функция f определена в некоторой окрестности точки x=a за исключением, быть может, самой точки a. Возьмем последовательность точек { x_n } из этой окрестности, сходящуюся к точке a. Значения функции в точках последовательности, в свою очередь, образуют последовательность f(x₁), f(x₂),..., f(x_n),.... Число b называется пределом функции f в точке x=a (или при x → a), если для любой последовательности { x_n }, сходящейся к a и такой, что x_n ̸=a для всех n ∈ N, соответствующая последовательность значений функции { f(x_n) } сходится к b. Другими словами, число b называется пределом функции f в точке x=a, если ∀{ x_n }, x_n ̸=a (n ∈ N), 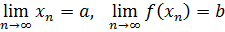. Данное определение называется определением предела функции по Гейне, или на языке последовательностей. Предел функции f в точке x = a обозначается следующим образом:

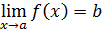
Определение. Число b называется пределом функции f при x →∞, или на бесконечности, если для любой ББП { x_n } соответствующая последовательность значений функции { f(x_n) } сходится к b. Для обозначения предела функции на бесконечности применяется запись:

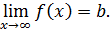
Пример 6.1. Постоянная функция f(x) = C в каждой точке имеет предел. Действительно, пусть a ∈ R и { x_n }—произвольная последовательность, сходящаяся к a. Тогда ∀ n ∈ N f (x_n) = C, и последовательность { f(x_n) } будет иметь своим пределом число C.

Пример 6.2. Функция f(x) = sin(π/x) определена всюду на R, за исключением точки x = 0. Выясним, существует ли предел этой функции в точке x=0. С этой целью возьмем следующие две последовательности. Пусть первую последовательность составляют числа x_n >0, где n = 0,1,2,..., такие, что sin(π/x_n)=1, т.е. π/x_n=(4n+1)π/2, x_n=2/(4n+1). Очевидно, последовательность { x_n } сходится к точке x = 0, а соответствующая последовательность значений функции будет состоять из единиц и иметь своим пределом число 1. Теперь возьмем другую последовательность значений аргумента { y_n }, где y_n > 0 и n ∈ N, такую, что sin(π/y_n)=0, т.е. π/y_n=nπ, y_n=1/n, n ∈ N. Очевидно, в этом случае последовательность значений аргумента { y_n } сходится к нулю, и соответствующая последовательность значения функции { sin(π/y_n)} также сходится к нулю. Таким образом, в первом случае последовательность значений функции сходится к 1, а во втором к 0. Это означает, что у функции f(x)=sin(π/x) в точке x=0 предел не существует.

6.2. Предел функции по Коши.

Имеет место и другое определение предела функции в точке.

Определение. Число b называется пределом функции f в точке x=a, если для любого числа ε>0, сколь малым оно бы ни было, существует положительное число δ такое, что для всякого x, удовлетворяющего условию 0<|x−a|<δ, выполняется неравенство |f(x)−b|<ε. Другими словами, число b называется пределом функции f в точке x = a, если ∀ ε>0 ∃ δ>0: ∀ x, 0<|x−a|<δ, |f(x)−b|<ε. Это определение называется определением предела функции по Коши, или на языке ε-δ.

Можно доказать, что определения предела функции по Гейне и по Коши равносильны. Определение предела функции по Коши можно переформулировать следующим способом.

Определение. Число b называется пределом функции f в точке x = a, если для любой ε-окрестности точки b найдется такая δ-окрестность точки a, что для всех x ̸= a из этой δ-окрестности соответствующие значения функции f(x) лежат в ε-окрестности точки b. Это определение называется определением предела функции на языке окрестностей и выражает геометрический смысл предела функции.

Теорема 6.1. Определение предела по Гейне эквивалентно определению предела по Коши.

Доказательство. Пусть число b является пределом функции 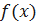 в точке a по Коши. Выберем произвольную подходящую последовательность 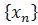, , 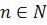то есть такую, для которой 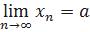. Покажем, что b является пределом по Гейне. Зададим произвольное  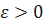и укажем для него такое 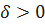, что для всех x из условия  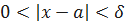следует неравенство 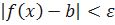. В силу того, что 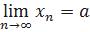, для 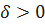 найдётся такой номер 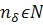, что 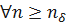 будет выполняться неравенство 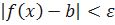, то есть .

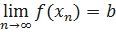Докажем теперь обратное утверждение: предположим, что 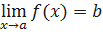 по Гейне, и покажем, что число b является пределом функции f (x) в точке a по Коши. Предположим, что это неверно, то есть: 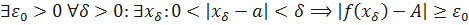. В качестве  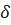рассмотрим 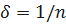, а соответствующие значения 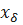будем обозначать 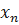. Тогда при любом  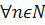выполняются условия  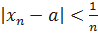и 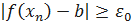. Отсюда следует, что последовательность  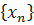является подходящей, но число b не является пределом функции  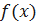в точке a. Получили противоречие.

Односторонние пределы.

Определение. Число 𝑐 называется правым пределом функции 𝑓 в точке 𝑥=𝑎, если для любой сходящейся к 𝑎 последовательности {𝑦_𝑛}, члены которой больше 𝑎, cсоответствующая последовательность {𝑓(𝑦_𝑛)} сходится к 𝑐. Символически это записывается следующим образом: 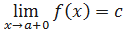. Аналогичным образом определяется левый предел.

Определение. Число 𝑏 называется левым пределом функции 𝑓 в точке 𝑥=𝑎, если ∀{𝑥_𝑛}, 𝑥_𝑛<𝑎 (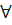 𝑛∈ N), 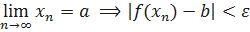. В этом случае применяется обозначение: 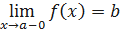. В случае, когда 𝑎=0, используются обозначения:  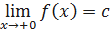и .

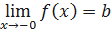Определение. Правый и левый пределы функции в точке называются односторонними.

Определение. Число 𝑏 называется пределом функции 𝑓 при 𝑥→+∞, если для любой такой ББП {𝑥_𝑛}, что 𝑥_𝑛>0 для всех 𝑛∈ N, соответствующая последовательность {𝑓(𝑥_𝑛)} сходится к 𝑏.

Аналогично определяется предел функции при 𝑥→−∞. Для записи таких преде