ПАРАДОКСЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. Под словом «парадоксы» в данном случае понимают те выводы из СТО, которые, хотя и являются совершенно правильными по существу и подтверждаются экспериментами, тем не менее противоречат интуитивным, основанным на классической физике представлениям.
1. Самый известный – парадокс близнецов обычно формулируется так. Пусть брат-близнец А отправляется в космический полет на звезду Х, находящуюся от нас на расстоянии, скажем, 20 световых лет. Скорость звездолета близка к скорости света: v = 0,9 с. Долетев до звезды примерно за 22,3 года (по своим часам), корабль разворачивается и летит обратно. Таким образом, по часам брата А, совершившего этот полет, прошло примерно T = 44,6 года. Второй брат-близнец Б дожидался возвращения брата А на Земле. У трапа звездолета брата А встретил дряхлый старец, которому пришлось ждать встречи более 100 лет.
Собственно, здесь еще нет парадокса. Действительно, при движении со скоростью v = 0,9 c лоренц-фактор равен g» 2,3 и вследствие эффекта замедления времени по часам земного наблюдателя прошло время, равное g T»103 года.
Парадокс возникает при попытке обратить рассуждение. Ведь с точки зрения брата А (неподвижный наблюдатель) движется брат Б, и по его часам проходит больше времени. Но с точки зрения брата Б движется брат А, и по его часамдолжно пройти больше времени. Таким образом, брат А должен вернуться постаревшим. Казалось бы, формулы СТО симметричны относительно замены v на – v. В чем же дело?
Этот парадокс разрешается следующим образом. Дело в том, что мировые линии братьев А и Б различны. Один из них (Б) находится в покое, другой (А) совершает движение с постоянной скоростью, которая в определенный момент изменяется на обратную, что возможно только при торможении и последующем ускорении космического корабля (что соответствует движению в неинерциальной системе отсчета). Таким образом, брат А движется от Земли и к Земле, находясь в покое сначала относительно одной инерциальной системы, а затем — относительно другой, и по дороге переходит на короткое время в неинерциальную систему. В то же время брат Б покоится относительно одной и той же инерциальной системы. Видно, что А и Б находятся в разных физических условиях, и это разрешает парадокс. Точный расчет показывает, что с точки зрения любого из братьев постареет больше тот, который неподвижен относительно Земли.
В ускорителях коротко живущие частицы, движущиеся со скоростями, близкими к скорости света, «живут» много дольше, чем «покоящиеся» частицы
2. Другой эффект – лоренцевское сокращение длины и связанные с ним парадоксы.
Пусть есть две инерциальные системы отсчета – S ' и S. В системе S ' жесткий стержень длиной D x ' покоится вдоль оси x и нужно определить его длину в системе S, относительно которой стержень движется со скоростью v. Чтобы измерить длину стержня в любой инерциальной системе, относительно которой стержень движется вдоль продольной оси, нужно одновременно наблюдать его концы. Это – ключевое положение, непонимание которого и приводит иногда к парадоксам.
В СТО нужно отличать то, что видит наблюдатель, от того, что он знает как бы пост-фактум. То, что наблюдатель видит или фотографирует в любой фиксированный момент времени, называется картиной мира в этот момент. Это понятие практически не очень важно, а теоретически очень сложно, т.к. то, что наблюдатель видит в данный момент, – это смесь событий, происходивших все дальше в прошлом и все дальше в пространстве.Если смотреть на ночное небо, полное звезд, то расстояния до этих звезд составляют от нескольких до сотен тысяч св. лет, следовательно, наблюдающий видит свет от этих звезд, испущенный в разное время и одновременно дошедший до его глаза, т.е он. видит разновременные события.
Колебания.
23. Дифференциальное уравнение гармонических колебаний и его решение (на примере пружинного маятника).
Частоту свободных гармонических колебаний называют собственной частотой (wо), т.к. она зависит только от свойств самой физической системы.
Найдем дифференциальное уравнение свободных гармонических колебаний пружинного маятника. На маятник (рис. 6.13) действует сила тяжести
G = mg,
де 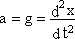 , и сила упругости
, и сила упругости
Fупр = – кх,
где х - смещение; k - коэффициент жесткости (упругости) пружины (см. п.3.36. Закон Гука).
Эти силы в состоянии покоя равны по величине, но противоположны по направлению (третий закон Ньютона). Однако при колебаниях сила упругости изменяется периодически по величине и по направлению. Значит силой, вызывающей колебания пружинного маятника, является сила упругости. При этом выполняется следующее соотношение:
ma = – kx
или
 . .
|
Последнее выражение приведем к нормальному виду однородного дифференциального уравнения второго порядка, описывающего одномерное (с одной степенью свободы) движение пружинного маятника, например, вдоль оси Х:
 . .
|
Решением данного дифференциального уравнения является функция
Выразим k в (6.25) через собственную круговую частоту wо и смещение х. Для этого достаточно вспомнить, что ускорение
 . .
|
Используя (6.23) и (6.26), запишем, что
С другой стороны при колебаниях пружинного маятника роль действующей силы выполняет сила упругости (речь о ней шла выше)
Из (6.27) и (6.28), имеем
- m wо2х = – кх.
После несложных преобразований получим
Дифференциальное уравнение (6.24) принимает следующий вид:
 . .
|
Напомним, что уравнение вида (6.30) является общим для всех физических систем различной природы, совершающих свободные гармонические колебания, только вместо смещения х используется величина, характеризующая колебания данной системы, например, колебание заряда (q), тока (I) и т.д.
Сравнивая общее дифференциальное уравнение гармонических колебаний (6.30) и дифференциальное уравнение колебаний пружинного маятника (6.24), приходим к заключению, что квадрат круговой частоты прямо пропорционален коэффициенту жесткости пружины и обратно пропорционален его массе:
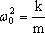 . .
|
Найдем период колебаний пружинного маятника. Из кинематики вращательного движения м.т. известно, что период и угловая скорость (круговая частота) связаны соотношением
 .
.
Следовательно, период колебаний пружинного маятника
 . .
|
24. Условия возникновения механических колебаний.
Хотя бы одна сила должна зависеть от координат.
При выведении тела из положения устойчивого равновесия возникает равнодействующая, направленная к положению равновесия. С энергетической точки зрения это значит, что возникают условия для постоянного перехода кинетической энергии в потенциальную и обратно.
Силы трения в системе малы.
Для возникновения колебания тело необходимо вывести из положения равновесия, сообщив либо кинетическую энергию (удар, толчок), либо – потенциальную (отклонение тела).
Примеры колебательных систем:
Нить, груз, Земля.
Пружина, груз.
Жидкость в U -образной трубке, Земля.
Струна.
Свободные колебания — это колебания, которые возникают в системе под действием внутренних сил, после того как система была выведена из положения устойчивого равновесия. В реальной жизни все свободные колебания являются затухающими (т.е. их амплитуда, размах, уменьшается с течением времени).
Вынужденные колебания – колебания, которые происходят под действием внешней периодической силы.
Характеристики колебательного процесса.
1. Смещение х - отклонение колеблющейся точки от положения равновесия в данный момент времени (м).
2. Амплитуда хм - наибольшее смещение от положения равновесия (м). Если колебания незатухающие, то амплитуда постоянна.
3. Период Т — время, за которое совершается одно полное колебание. Выражается в секундах (с).
За время, равное одному периоду (одно полное колебание) тело совершает перемещение, равное 0 и проходит путь, равный 2πr.
4. Частота ν — число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц).
Частота колебаний равна одному герцу, если за 1 секунду совершается 1 полное колебание. 1 Гц= 1 с-1.
5. Циклической (круговой) частотой ω периодических колебаний наз. число полных колебаний, которые совершаются за 2π единиц времени (секунд). Единица измерения – с-1.
6. Фаза колебания - φ - физическая величина, определяющая смещение x в данный момент времени. Измеряется в радианах (рад).
Фаза колебания в начальный момент времени (t=0) называется начальной фазой (φ0).
25. Энергия гармонических колебаний.
При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:

(Скорость тела v = ds/dt)
Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:

где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.
Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:




|
| для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы: Сравнивая формулы
 
|
1. Полная механическая энергия тела не изменяется при колебаниях: 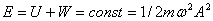
2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.
3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на p (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.
В случае электрических колебаний энергия в конуре представляет собой сумму энергии электрического поля, запасенной между обкладками конденсатора, и энергии магнитного поля, запасенной в катушке с индуктивностью. Вычислим обе составляющие.


Сравнивая эти формулы, можно сделать следующие выводы:
1. Полная энергия в контуре остается неизменной: 
2. Частота колебаний энергий в 2 раза превосходит частоту колебаний заряда и тока в контуре.
3. Электрическая и магнитная энергии сдвинуты по фазе на полпериода друг относительно друга; происходит непрерывное перекачивание энергии из одной формы в другую и обратно.
Поскольку в контуре происходят колебания электрической и магнитной энергий, электрический колебательный контур также называют электромагнитным.
26. Дифференциальное уравнение колебаний пружинного маятника в вязкой среде. Логарифмический декремент затухания. Добротность.
Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.
Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.
Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения

где r - коэффициент сопротивления среды. Знак минус показывает, что FC направлена в сторону противоположную скорости.
Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r. По второму закону Ньютона




где β - коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.

- дифференциальное уравнение затухающих колебаний.

- уравнение затухающих колебаний.
ω – частота затухающих колебаний:

Период затухающих колебаний:

 Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало.
Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало.
Если затухания выражены слабо (β→0), то  . Затухающие колебания можно
. Затухающие колебания можно
рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону

В уравнении (1) А0 и φ0 - произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания

Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз





τ - время релаксации.
Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D, который равен отношению амплитуд, отстоящих по времени на период:

Логарифмический декремент затухания равен логарифму D:


Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз. Логарифмический декремент затухания - постоянная для данной системы величина.
Еще одной характеристикой колебательной система является добротность Q.

Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.
Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.
Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.
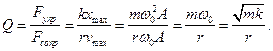
Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.
§7 Вынужденные колебания.
Резонанс
В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.
Пусть
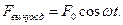
Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.
По второму закону Ньютона:




 (1)
(1)
- дифференциальное уравнение вынужденных колебаний.
Это дифференциальное уравнение является линейным неоднородным.
Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:


Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:
 (2)
(2)
Частное решение этого уравнения будем искать в виде:

Тогда


Подставим в (2):

т.к. выполняется для любого t, то должно выполняться равенство γ = ω, следовательно,

Это комплексное число удобно представить в виде

где А определяется по формуле (3 ниже), а φ - по формуле (4), следовательно, решение (2),в комплексной форме имеет вид

Его вещественная часть, являвшаяся решением уравнения (1) равна:

где
 (3)
(3) 
 (4)
(4)
Слагаемое Хо.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме в  ынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механической системы, называется резонансом.
ынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механической системы, называется резонансом.
Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ωрез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).


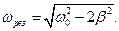
Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то
ωрез = ω0.
При ω→0 все кривые приходят к значению  - статическое отклонение.
- статическое отклонение.

Параметрический резонанс возникает в том случае, когда периодическое изменение одного из параметров система приводит к резкому увеличению амплитуды колеблющейся системы. Например, кабины, делающие "солнышко" за счет изменения положения центра тяжести система.(То же в "лодочках".) См. §61.т. 1 Савельев И.В.
Автоколебаниями называются такие колебания, энергия которых периодически пополняется в результате воздействия самой системы за счет источника энергии, находящегося в этой же системе.



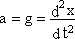 , и сила упругости
, и сила упругости .
.
 .
.
 .
.
 .
.
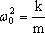 .
.
 .
. .
.








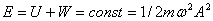












 Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало.
Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало. . Затухающие колебания можно
. Затухающие колебания можно










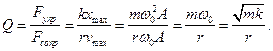
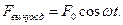


 (1)
(1)

 (2)
(2)







 (3)
(3) 
 (4)
(4) ынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механической системы, называется резонансом.
ынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механической системы, называется резонансом.

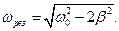
 - статическое отклонение.
- статическое отклонение.



