

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
Топ:
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Если угловое ускорение  постоянно, то
постоянно, то
 (24)
(24)
и
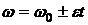 , (25)
, (25)
 и
и  – угловая скорость и угол поворота тела в начальный момент
– угловая скорость и угол поворота тела в начальный момент  ,
,
 и
и  – в момент времени
– в момент времени  . При ускоренном вращении в уравнениях (24) - (25) выбирается знак «+», а при замедленном – знак «-».
. При ускоренном вращении в уравнениях (24) - (25) выбирается знак «+», а при замедленном – знак «-».
9.Моменты силы. Момент импульса
Моментом силы называют вращательное усилие создаваемое вектором силы относительно другого объекта.
Размерность - [Н⋅м] (Ньютон на метр) либо кратные значения [кН⋅м]
Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.
Определяется как произведение силы на плечо:
M(F)=F⋅h
Здесь h - плечо момента, определяется как кратчайшее расстояние от точки до линии действия силы.
Рассмотрим порядок определения плеча h момента на примере:
Пусть заданы точка A и некоторая произвольная сила F. Требуется определить момент создаваемый силой F относительно точки A.

Покажем линию действия силы F (штриховая линия)

Проведем из точки A перпендикуляр h к линии действия силы

Длина отрезка h есть плечо момента силы F относительно точки A.
Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).
Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.
Момент импульса
Векторное произведение радиуса-вектора  материальной точки на ее импульс:
материальной точки на ее импульс:  называют моментом импульса
называют моментом импульса  , этой точки относительно точки О (рис.5.4)
, этой точки относительно точки О (рис.5.4)

 . Вектор
. Вектор  иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы
иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы  и
и  и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от
и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от  к
к  происходит против часовой стрелки).
происходит против часовой стрелки).
|
|
Векторную сумму моментов импульсов  всех материальных точек системы называют моментом импульса (количества движения)
всех материальных точек системы называют моментом импульса (количества движения)  системы относительно точки О:
системы относительно точки О:

Векторы  и
и  взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому
взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому  . Сучетом связи линейных и угловых величин
. Сучетом связи линейных и угловых величин

и направлен вдоль оси вращения тела в ту же сторону, что и вектор 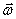 .
.
Таким образом.

Момент импульса тела относительно оси вращения

т.е.
 (5.9)
(5.9)
Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси.
10. Закон сохранения момента импульса
Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси. Значение момента импульса Lz не зависит от положения точки 0 на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдельная точка тела движется по окружности постоянного радиуса ri с некоторой скоростью vi. Скорость vi и импульс mivi перпендикулярны этому радиусу, т.е. радиус является плечом вектора mivi. Поэтому можно записать, что момент импульса отдельной точки относительно оси z равен

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его точек:
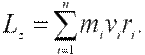
Учитывая связь между линейной и угловой скоростями (vi = ωri), получим следующее выражение для момента импульса тела относительно неподвижной оси:
 (4.12)
(4.12)
т.е. момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
Продифференцировав выражение (4.12) по времени, получим:
 (4.13)
(4.13)
Это еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всех внешних сил, действующих на тело.
Закон сохранения момента импульса вытекает из основного уравнения динамики вращательного движения тела, закрепленного в неподвижной точке (уравнение 4.8), и состоит в следующем:
если результирующий момент внешних сил относительно неподвижной точки тождественно равен нулю, то момент импульса тела относительно этой точки с течением времени не изменяется.
Действительно, если M = 0, то dL / dt = 0, откуда
|
|
 (4.14)
(4.14)
Другими словами, момент импульса замкнутой системы с течением времени не изменяется.
Из основного закона динамики тела, вращающегося вокруг неподвижной оси z (уравнение 4.13), следует закон сохранения момента импульса тела относительно оси:
если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется в процессе движения, т.е. если Mz = 0, то dLz / dt = 0, откуда
 (4.15)
(4.15)
Закон сохранения момента импульса является фундаментальным законом природы. Справедливость этого закона обусловливается свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета.
Справедливость закона сохранения момента импульса относительно неподвижной оси вращения можно продемонстрировать на опыте со скамьей Жуковского. Скамьей Жуковского называется горизонтальная площадка, свободно вращающаяся без трения вокруг неподвижной вертикальной оси ОО1. Человек, стоящий или сидящий на скамье, держит в вытянутых руках гимнастические гантели и приводится во вращение вместе со скамьей вокруг оси ОО1 с угловой скоростью ω1. Приближая гантели к себе, человек уменьшает момент инерции системы, а так как момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость ее вращения ω2 возрастает. Тогда по закону сохранения момента импульса относительно оси ОО1 можно записать:
 (4.16)
(4.16)
где J0 - момент инерции человека и скамьи; 2 mr12 и 2 mr22 - моменты инерции гантелей в первом и втором положениях; m – масса одной гантели; r1, r2 – расстояния от гантелей до оси ОО1.
Изменение момента инерции системы связано с изменением ее кинетической энергии:
|
|

Используя выражение для ω2, полученное из (4.16)

после преобразований получим:

Это изменение кинетической энергии системы численно равно работе, совершенной человеком при перемещении гантелей.
В табл. 4.2 сопоставлены основные физические величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение.
Таблица 4.2

Краткие выводы
Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
Момент инерции тела относительно оси вращения – это физическая величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний до рассматриваемой оси:

Момент инерции тела Jz относительно любой оси вращения равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:

При вращении абсолютно твердого тела вокруг неподвижной оси z его кинетическая энергия равна половине произведения момента инерции относительно оси вращения на квадрат угловой скорости:

Из сравнения формул 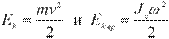 следует, что момент инерции – мера инертности тела при вращательном движении.
следует, что момент инерции – мера инертности тела при вращательном движении.
Работа вращения тела идет на увеличение его кинетической энергии и определяется выражением dA = Mzdφ, где Mz – момент сил относительно оси вращения z.
Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z (аналог второго закона Ньютона) имеет вид:

где Lz – момент импульса твердого тела относительно оси z.
В замкнутой механической системе момент внешних сил относительно неподвижной оси Mz = 0 и dLz / dt = 0, откуда Lz = const – закон сохранения момента импульса. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.
Механика твердого тела
1. Поступательным называется такое движение абсолютно твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки. В самом общем случае поступательно движущееся твердое тело обладает тремя степенями свободы.
2. Движение абсолютно твердого тела, при котором две его точки А и B остаются неподвижными, называется вращением (вращательным движением) вокруг неподвижной прямой АВ, называемой осью вращения. При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности, центры которых лежат на оси вращения, а плоскости - перпендикулярны к ней. Тело, вращающееся вокруг неподвижной оси, обладает одной степенью свободы: его положение полностью определяется заданием угла f поворота из некоторого начального положения.
3. Угловой скоростью вращения твердого тела называется вектор w, численно равный первой производной от угла поворота по времени,
w = df/dt
|
|
и направленный вдоль оси вращения таким образом, чтобы из его конца вращение тела было видно происходящим против часовой стрелки. Направление вектора w совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом.
4. Линейная скорость v произвольной точки М вращающегося тела определяется как векторное произведение по формуле Эйлера
v = [wr]
где r - радиус-вектор, проведенный в точку М из произвольной точки О оси вращения тела. Численное значение v линейной скорости точки М прямо пропорционально ее расстоянию R от оси вращения:
v = wr sina = wR
где a - угол между векторами w и r.
5. Периодом обращения Т тела называется время, в течение которого тело поворачивается вокруг неподвижной оси вращения на угол f = 2p.
6. Угловым ускорением называется вектор e, равный первой производной от вектора угловой скорости по времени:
e = dw/dt
Угловое ускорение характеризует быстроту изменения во времени вектора угловой скорости тела. При вращении вокруг неподвижной оси направление вектора w сохраняется и
e = dw/dt = d2f/dt2
причем вектор e совпадает но направлению с w в случае ускоренного вращения (e > 0) и противоположен ему по направлению в случае замедленного вращения (e < 0)
Линейное ускорение произвольной точки М (r) вращающегося тела равно
a = dv/dt = d/dt | wr | = | er | + | w | wr ||
|
|
|

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!