Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы А на число k.



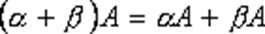 - Cв-ва.
- Cв-ва.
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,


 - размеры разл.
- размеры разл.
Сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).
1. Умножение матриц
Матр А и В соглас-е, если число строк матр А равно числу столбцов матр В, и наоборот.
Оп-ция умн-я матриц определена только для соглас. матриц.
Кв матрицы одного и того же порядка и одной и той же размерности всегда согласованны.
Пусть задана матр А=aik i=1,m; k=1,n и матр В=bkj k=1,m; j=1,n. Тогда произв-ем А на В наз. матр С такая, что сik=ai1·b1k+ ai2·b2k +…+ ain·bnk, где i=1,m; k=1,n, т.е. эл-т i-той строки и k-того столбца матрицы произв-ия С равен ∑ произв-ий эл-ов i-той строки матр А на соответствующие эл-ты k-того столбца матр В.
Если выполняется равенство АВ=ВА, то матрицы А и В наз. перестановочными (коммутирующими)
Матр,получ. из данной заменой кажд ее строки столбц с тем же номером,наз. транспон-ой к данной.
Св-ва умножения:
1.А·(ВС)=(АВ)С
2. А(В+С)=АВ+ВС
3. (А+В)С=АС+ВС
4. α(АВ)=(αА)В
Св-ва транспонирования:
1.(А+В)т=Ат+Вт
2. (АВ)т=В·Ат
3. (Ат) т= А
Квадратная матрица А, которая не меняется при транспонировании, - симметричная.
 Если матрица симметрична, то эл-ты, равноудаленные от главной диагонали, совпадают.
Если матрица симметрична, то эл-ты, равноудаленные от главной диагонали, совпадают.
А= 2 5 -2
5 -7 3
-2 3 1
Опред-ль 1,2,3 порядков.
Квадратной матрице А порядка n можно сопоставить число det A, называемое ее определителем следующим образом:
1. n=1. A=(a1); det A=a1
2. n=2.
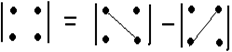
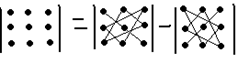
3. n=3.
Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали: 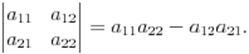
Определителем третьего порядка называется следующее выражение: 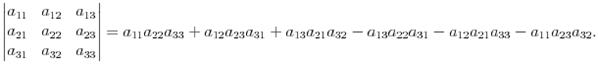 Правило треугольников:
Правило треугольников: 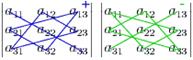
Пример: А= 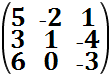 det A= 5×1×(-3)+(-2)×(-4)×6+3×0×1- 6×1×1-3×(-2)×(-3)-0×(-4)×5=-15+48-6-18=9
det A= 5×1×(-3)+(-2)×(-4)×6+3×0×1- 6×1×1-3×(-2)×(-3)-0×(-4)×5=-15+48-6-18=9
3. Определитель квадратной матрицы порядка n.
Определитель квадратной матрицы n-ного порядка равен алгебраической сумме парных произведений элементов i-той строки матрицы А на их алгебраические дополнения или j-го столбца на их алгебраические дополнения.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения
4. Свойства определителей.
Если к.-л. строка или столбец в матрице состоит из одних нолей, то det
Этой матрицы равен 0
2)При транспонировании матрицы её определитель не изменяется: (detА =detА')
При перестановке местами 2-х строк или столбцов матрицы её
Определитель меняет свой знак на противоположный
Доказательство – проверкой.
9) det верхней треуг. матрицы = произведению диагональных эл-тов.
10) det A*B=detA*detB
Выбираем в матрице произвольные k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка k. Определитель полученной матрицы называется минором k-го порядка матрицы А.
Наибольший из порядков миноров данной матрицы, отличный от нуля, называется рангом матрицы. (обозначается r(A))
нек. св-ва: 1) r(A)=0 => A=0
2) 
3) ранг верхней треугольной м. = числу диагональных эл-тов гл. диагонали неравных нулю.
ранг трапециевидной матрицы= числу диагональных эл-тов главного базисного минора.
Теорема Кронекера-Капелли
Для того, чтобы СЛАУ, где AX=B, где матр A разм-ти m*n была совместной необх-мо и дост-но, чтобы ранг осн матр системы был равен рангу расшир матр системы.
r(A) = r(A/B)
Док-во:
Необходимость: пусть СЛАУ AX=B совместна.
Доказать, что ранги равны.
Сущ набор чисел (α1, α2…..αn), что будучи подставл в каждое из ур-й системы получим:
Матричный метод
Пусть дана система из 3-х уравнений с тремя неизвестными  .
.  Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A:. Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A:. Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.
Метод Крамера.
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:  Находим det
Находим det
 Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов  Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём 
10.Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
· перестановка строк или столбцов;
· умножение строки на число, отличное от нуля;
· прибавление к одной строке другие строки.
· Удаление нулевой строки
Приведение системы к ступенчатому виду или расширенную матрицу к виду трапециевидной называется прямой ход Гаусса. Обратный ход – неизвестные определяются последовательно, начиная с последнего неизвестного и кончая первым. Придавая неизвестным (называемым свободными) произвольные значения, получим треугольную систему из которой последовательно найдем все остальные неизвестные (называемые базисными).
11. Понятие об n-мерном векторе. Векторное пространство.
Вектор – направленный отрезок на плоскости или в пространстве, имеющий определённую длину, у которого одна из точек принята за начало, а другая за конец. Длиной вектора (нормой) или модулем называется число, равное длине отрезка, изображающего вектор [ïaï=Öx2+y2(+z2)]. Если начало и конец вектора совпадают, то такой вектор называется нулевым и обозначается `0. Для каждого `а, отличного от 0, существует противоположный -`а, который имеет модуль, равный ïаï, коллиниарен с ним, но направлен в другую сторону. Два вектора `а и`в называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Два вектора называются равными, если они: 1)имеют равные модули; 2)коллиниарны; 3)направлены в одну сторону.
n-мерный вектор- упорядоченный набор n чисел, где каждое из n чисел- соответствующие координаты вектора. x=(x1,x2,xi,xn) Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее всем сво-вам суммы(коммутативное, ассоциативные), называется векторным пространством. Размерность векторного пространства равна количеству векторов в базисе этого пространства. Совокупность n-мерных векторов, рассматриваемая с определёнными в ней операциями сложения векторов и умножения вектора на число, называется n-мерным координатным пространством. Система n—мерных лин. независимых векторов называется базисом Rn (R2-плоскость,R3-пространство), если каждый вектор этого пространства R разлагается по векторам этой системы. Базисом называется совокупность всех лин. независимых векторов системы пространства. Теорема: если диагональная система является частью n-мерных векторов, то она же является базисом этой системы. Теорема: любой вектор системы векторов единственным образов разлагается по векторам её базиса.
12. Линейная зависимость векторов.
Векторы  называются линейно зависимыми, если существует такая линейная комбинация
называются линейно зависимыми, если существует такая линейная комбинация  при не равных нулю одновременно
при не равных нулю одновременно  . Если же только при ai = 0 выполняется
. Если же только при ai = 0 выполняется  , то векторы называются линейно независимыми.
, то векторы называются линейно независимыми.
Общее уравнение плоскости.
Ax+By+Сz-Ax0-By0-Сz0=0
-Ax0-By0-Сz0=D, где D=Ax+By+Сz
Ax+By+Сz+D=0
16. Углом между двумя прямыми называется любой из двух углов, образованных прямыми при их пересечении.
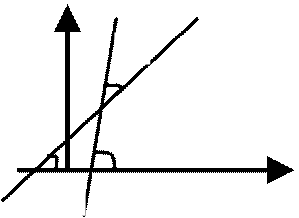
θ=α2- α1
tgθ=tg(α2-α1)= (tgα2 – tgα1)/(1+ tgα2*tgα1)= (k2-k1)/(1+k2*k1)
tgθ=(k2-k1)/(1+k2*k1) – формула для вычисления угла между двумя пересекающимися прямыми
1. пусть θ=0, тогда прямые параллельны, tgθ=0 след-но k1=k2 – условие параллельности прямых
2. θ=90о, то tg θ= ∞ или не существует
1+k1* k2=0
k1* k2= -1 – условие перпендикулярности прямых
17. Расстояние от точки до прямой
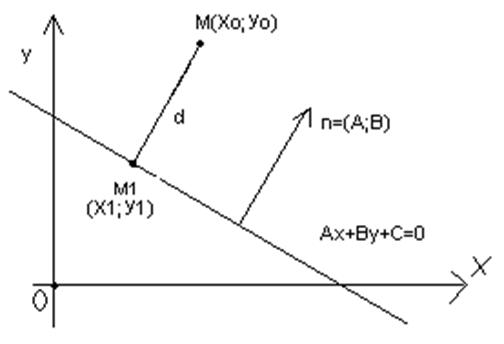
 Пусть задана прямая Ах+Ву+С=0 и точка М0(х0;у0), не лежащая на прямой. Нужно найти расстояние от точки М0 до прямой.
Пусть задана прямая Ах+Ву+С=0 и точка М0(х0;у0), не лежащая на прямой. Нужно найти расстояние от точки М0 до прямой. 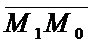 коллинеарна
коллинеарна 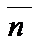 . (
. (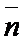 ;
; 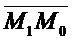 )=А(х1 – х0)+В(у1-у0). (
)=А(х1 – х0)+В(у1-у0). (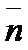 ;
; 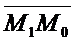 )=
)= 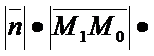 cos
cos 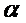 =
= 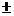
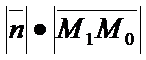 . А(х1 – х0)+В(у1-у0)=
. А(х1 – х0)+В(у1-у0)= 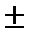
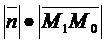 .
.
d= 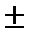
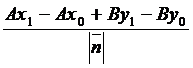 =
= 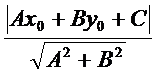 ------- формула для вычисления расстояния от точки до прямой, С=Ах1 +Ву1.
------- формула для вычисления расстояния от точки до прямой, С=Ах1 +Ву1.
ИЛИ Не из конспекта: d= 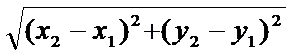 .
.
18. Понятие о кривых 2-го порядка. Окружность, эллипс, гипербола, парабола.
Кривые 2го порядка описываются с помощью общего ур-я:
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где
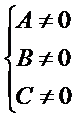
а) Каноническое ур-е эллипса
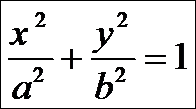 - Каноническое ур-е эллипса
- Каноническое ур-е эллипса
Если a=b, то x2+b2=a2 - ур-е окружности.
б) Ур-е гиперболы: x2/a2-y2/b2=1
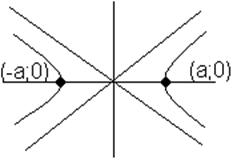
в) ур-е параболы: y2=2px или y=ax2
г) ур-е сферы: x2+y2+z2=а2 (r2=(x-a)2+(y-b)2+(z-c)2)
д) ур-е эллипса: x2/a2-y2/b2+z2/c2=1
18. Окружность
Это частный случай эллипса. Формула: (х-х0)2+(у-у0)2=R2, где (х0;у0)- координаты центра окружности.
Эллипс, его характеристики, геометрические свойства.
Э.—это геометрическое место точек плоскости, для которых сумма расстояний до двух заданных точек (фокусов) есть величина постоянная (и равна 2а).
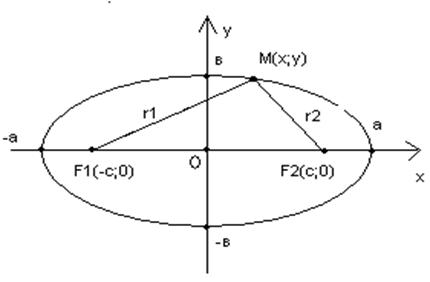
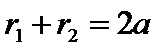 .
. 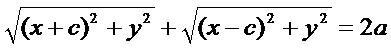 … b2=а2-с2
… b2=а2-с2
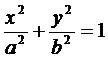 --каноническое уравнение, где a-большая полуось, b-меньшая полуось.
--каноническое уравнение, где a-большая полуось, b-меньшая полуось.
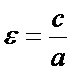 --- эксцентриситет эллипса. с2=а2-b2.
--- эксцентриситет эллипса. с2=а2-b2. 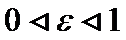 .
.
Прямые 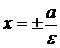 называются директрисами Э., параллельны Оу, лежат вне Э.
называются директрисами Э., параллельны Оу, лежат вне Э.
F1(-c;0), F2(c;0) координаты фокусов Э. 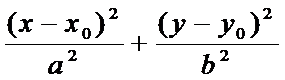 =1 также каноническое уравнение Э. с центром в т.(х0;у0).
=1 также каноническое уравнение Э. с центром в т.(х0;у0).
18а. Гипербола, ее характеристики, геометрические свойства
Г.—это геометрическое место точек плоскости, для которых модуль разности расстояний от двух заданных точек (фокусов) есть величина постоянная (и равна 2а).
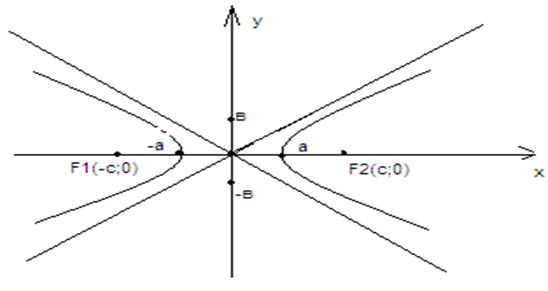
Пусть М(х;у) произвольная точка гиперболы, тогда согласно определнию: 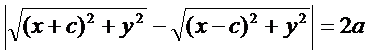
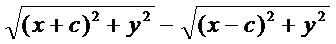 =
= 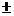 2а... с2-а2=в2
2а... с2-а2=в2
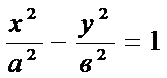 --- каноническое уравнение Г.
--- каноническое уравнение Г.
Это точка M0(x0,y0,z0)
Это точка M(x,y,z)
вектор M0M=(x-x0;y-y0;z-z0)
Векторы M0M//S
(x-x0)/k=(y-y0)/e=(t-t0)/m это каноническое
Введем параметр t Є R и положим (x-x0)/k=(y-y0)/e=(z-z0)/m=t, t Є R
x=x0+kt
y=y0+et это все параметрич ур-я прямой в пр-ве
z=z0+mt
 Ур-я вида
Ур-я вида
A1x+B1y+C1Z+D1=0 это общие ур-я
A2x+B2y+C2Z+D2=0 прямой в пространстве
Условие перпенд-ти

Если пр перп-на пл-ти,то ее направл в-р S кол-н норм в-ру пл-ти S//N A/k=B/e=C/m
Условие принадлежности прямой к плоскости:
Ax0+By0+Cz0+D=0 Ak+Be+Cm=0
21. Предел числовой последовательности (ЧП).
ЧП – это ф-ия натур аргумента xn=f(n),где n принадлежит N.
x1, x2,…xn,…-числ послед.(1), xn-общ член ЧП.
Число а наз пределом посл-ти, если для любого малого положит числа ξ > 0 сущ такой номер N, зависящий от ξ, что для всех номеров n>N выполняется неравенство |xn-а|< ξ.
Замечание. |xn-а|< ξ=> а- ξ<x1<а+ ξ, Xn- ξ<a<xn+ ξ – ξ окрестности т.а
Если число а-предел ЧП(1), то все члены посл-ти, начиная с некот номера N, попадают в ξ-окрестность т.а.Чем больше N,тем ниже а.
Если а-предел числ. послед-ти(1), то пишут: lim xn=a или xn→a, n→∞
Свойства числ. последовательности:
1.Если ЧП с общ членом xn имеет предел, то она наз сходящейся.Всякая сход посл-ть огран, т.е. сущ M>0, что все члены этой П по модулю не превосх это число. |xn |<М
2. Пусть заданы 3 П, xn, yn, zn-общие члены. Причем lim xn= lim zn=а и выполняется неравенство: xn ≤yn≤zn, то lim yn=а.
3. Пусть послед. xn, yn имеют конечные пределы lim xn=а lim yn=в -∞<а,в<+∞. Тогда:
a) lim(xn±yn)= limxn ± lim yn)-справ для люб кон числа П
b) lim(xn*yn)= limxn*limyn
c) lim(Cxn)=C limCxn=C*a.
d) lim  =
=  =
=  , b≠0.
, b≠0.
Посл αn наз бескон малой, если ее предел = 0, т.е. limαn=0
Послед. βn наз бесконечно большой, если ее предел = ∞.
Утверждение. Если послед. αn-беск. малая, то послед.  - беск. большая и наоборот.В курсах матанализа док-ся, что П {Хn}=
- беск. большая и наоборот.В курсах матанализа док-ся, что П {Хn}= 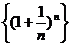 монот и огранич.По теореме: для того, чтобы монот сходилась, необхмо и достаточно, чтобы она была огранич. След-но, эта П имеет предел. Он обозначается буквой е: е=lim
монот и огранич.По теореме: для того, чтобы монот сходилась, необхмо и достаточно, чтобы она была огранич. След-но, эта П имеет предел. Он обозначается буквой е: е=lim  , причем е=2,718.
, причем е=2,718.
Замечат пределы.
1-й замечат предел, или тригонометрич предел. 
Теорема:

Док-во:

 ;
; 
Очевидно: 

sinx<=x<=tgx
Т.к. 
 ;
;  ;
;

Следствия из теоремы:
1.  2.
2. 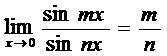
Второй замечательный предел:


Е-число Эйлера,


Если 



26. Непрерывность функции в точке. Точки разрыва и их классификация.
Пусть у=f(x) задана в некотором множестве х, тогда функция называется непрерывной в точке  , если
, если 
 , x
, x 
 x
x 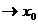
т. е. функция f(x) называется непрерывной в точке  , если она определена в этой точке, односторонние пределы существуют, являются конечными цифрами между собой и равны значению функции в этой точке.
, если она определена в этой точке, односторонние пределы существуют, являются конечными цифрами между собой и равны значению функции в этой точке.
Если у=f(x) непрерИвна в каждой точке множества х, то она непрерИвна на этом множестве.
Т.е. f’(
F’(
Пусть задана ф-ция S=S(t), кот. опред-ет зависимость пути от времени,в механике S’(t)=V –мгнов.скорость в момент времени t.
Пусть задана ф-ция у=f(x), для которой сущ-ет производная у’=f’(x). Эластич-тью ф-ции у=f(x) относ-но переменной х назыв-ся предел: 
Его обознач-т

Эластич-ть относ-но х есть приближен.процентн прирост ф-ции (повышение/пониж-е) при приращении независ переменной на 1%.
29. Производная показательной неявной функции.Производные высших порядков:
Производная показательной функции:
При 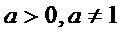 для любого х
для любого х

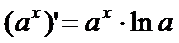
Производная неявной функции:
При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение 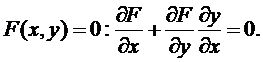 . Отсюда получим формулу для производной функции
. Отсюда получим формулу для производной функции 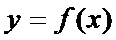 , заданной неявно:
, заданной неявно: 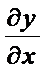 =
= 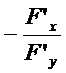 . Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением
. Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением 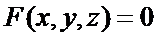 :
:
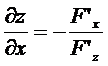 ,
, 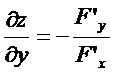 .
.
Производные высших порядков:
Если f '(x) — производная функции f (x), то производная от нее по независимой переменной x, (f '(x))' = f ''(x), называется производной второго порядка. Аналогично определены производные 3-го, 4-го,, и т.д, n-го порядка: f''' (x) = (f'' (x))', f (4)(x) = (f''' (x))', f (n)(x) = (f (n -1)(x))'
30. Теорема Лагранжа. Правило Лопиталя.
Теорема Лагранжа: Пусть задана ф-я 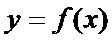 и пусть она: 1) опр-на и непрер на
и пусть она: 1) опр-на и непрер на 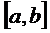 ; 2) имеет кон произв-ю
; 2) имеет кон произв-ю 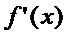 на
на 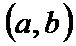 . Тогда найдётся такая т. с (a<c<b), что вып-ся рав-во
. Тогда найдётся такая т. с (a<c<b), что вып-ся рав-во
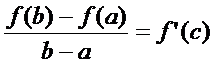 Док-во: Введём вспомогат функцию
Док-во: Введём вспомогат функцию
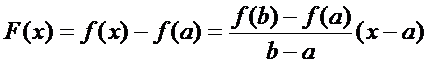
Она удовл-т всем условиям теоремы Ролля. Действительно, F(x) опред-на и непрер на 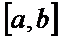 ,
, 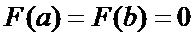 ,
,
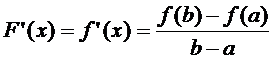 ,т.е. сущ на
,т.е. сущ на 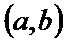 . След-но, найдётся точка с (a<c<b), такая, что F’(c) = 0, т.е.
. След-но, найдётся точка с (a<c<b), такая, что F’(c) = 0, т.е.
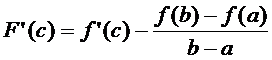 или
или 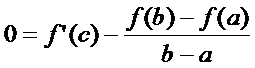
Тогда 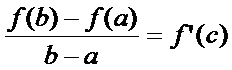 ∆
∆
Правило Лопиталя: Пусть ф-и f(x) и g(x) одновр явл либо бескон б-ми, либо беск-но малыми в т. 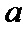 . Тогда при выч-и пределов
. Тогда при выч-и пределов 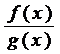 при x →
при x → 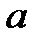 для раскрытия неопред-тей вида
для раскрытия неопред-тей вида  или
или 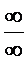 удобно применить пр. Лопиталя:
удобно применить пр. Лопиталя:
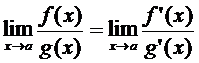 ,
, 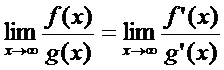 Неопределенности вида 0 · ∞, ∞ – ∞,
Неопределенности вида 0 · ∞, ∞ – ∞, 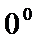 ,
, 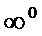 ,
, 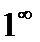 часто удается свести к неопределенностям вида
часто удается свести к неопределенностям вида 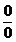 или
или  с помощью различных преобразований.
с помощью различных преобразований.
31. Достаточное усл-е возраст-я (убыв-я) ф-й.
Ф-я 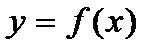 наз-ся возраст-ей на инт-ле
наз-ся возраст-ей на инт-ле 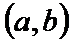 , если для любых
, если для любых 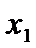 и
и 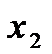 из этого инт-ла, для которых
из этого инт-ла, для которых 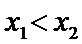 , верно нерав-во
, верно нерав-во 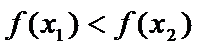 . Ф-я
. Ф-я 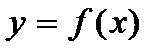 наз-ся убыв-ей на инт-ле
наз-ся убыв-ей на инт-ле 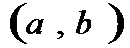 , если для любых x 1 и x 2 из этого инт-ла, для кот
, если для любых x 1 и x 2 из этого инт-ла, для кот 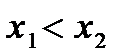 , верно нерав-во
, верно нерав-во 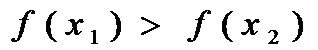 . Необх-ое усл-е возраст-я ф-ии:е сли ф-ия
. Необх-ое усл-е возраст-я ф-ии:е сли ф-ия 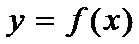 диффер-ма и возраста на инт-ле
диффер-ма и возраста на инт-ле 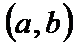 , то
, то 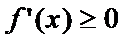 для всех х из этого инт-ла. Необх-ое усл-е убыв-я ф-ции. Если ф-ция
для всех х из этого инт-ла. Необх-ое усл-е убыв-я ф-ции. Если ф-ция 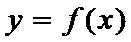 дифф-ма и убыва на инт-ле
дифф-ма и убыва на инт-ле 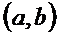 , то
, то 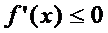 для всех х из этого инт-ла. Достаточное усл-е возраст-я (убыв-я ф-и). Пусть ф-я
для всех х из этого инт-ла. Достаточное усл-е возраст-я (убыв-я ф-и). Пусть ф-я 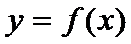 диф-ма на инт-ле
диф-ма на инт-ле 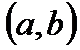 . Если во всех точках этого инт-ла
. Если во всех точках этого инт-ла 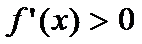 , то ф-ия возраста на этом интле, а если
, то ф-ия возраста на этом интле, а если 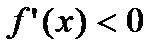 , то ф-я убывает на этом инт-ле.
, то ф-я убывает на этом инт-ле.
32. Экстремумы ф-й.
Точка x = x0 называется точкой максимума, а число 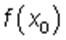 — максимумом функции, если для всех точек из некоторой окрестности точки x0, не совпадающих с x0, выполняется неравенство
— максимумом функции, если для всех точек из некоторой окрестности точки x0, не совпадающих с x0, выполняется неравенство 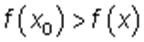 .
.
Точка x = x0 называется точкой минимума, а число 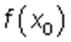 — минимумом функции, если для всех точек из некоторой окрестности точки x0, не совпадающих с точкой x0, выполняется неравенство
— минимумом функции, если для всех точек из некоторой окрестности точки x0, не совпадающих с точкой x0, выполняется неравенство 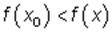 .
.
Находится производная.
Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы А на число k.



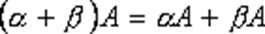 - Cв-ва.
- Cв-ва.
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,


 - размеры разл.
- размеры разл.
Сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).
1. Умножение матриц






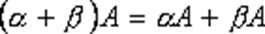 - Cв-ва.
- Cв-ва.

 - размеры разл.
- размеры разл. Если матрица симметрична, то эл-ты, равноудаленные от главной диагонали, совпадают.
Если матрица симметрична, то эл-ты, равноудаленные от главной диагонали, совпадают.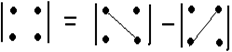

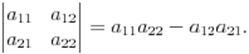
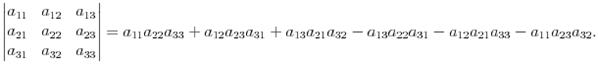 Правило треугольников:
Правило треугольников: 
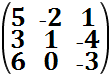 det A= 5×1×(-3)+(-2)×(-4)×6+3×0×1- 6×1×1-3×(-2)×(-3)-0×(-4)×5=-15+48-6-18=9
det A= 5×1×(-3)+(-2)×(-4)×6+3×0×1- 6×1×1-3×(-2)×(-3)-0×(-4)×5=-15+48-6-18=9

 .
.  Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A:. Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A:. Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B. Находим det
Находим det Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов  Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём 
 называются линейно зависимыми, если существует такая линейная комбинация
называются линейно зависимыми, если существует такая линейная комбинация  при не равных нулю одновременно
при не равных нулю одновременно  . Если же только при ai = 0 выполняется
. Если же только при ai = 0 выполняется  , то векторы называются линейно независимыми.
, то векторы называются линейно независимыми.

 Пусть задана прямая Ах+Ву+С=0 и точка М0(х0;у0), не лежащая на прямой. Нужно найти расстояние от точки М0 до прямой.
Пусть задана прямая Ах+Ву+С=0 и точка М0(х0;у0), не лежащая на прямой. Нужно найти расстояние от точки М0 до прямой. 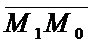 коллинеарна
коллинеарна 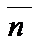 . (
. (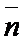 ;
; 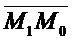 )=А(х1 – х0)+В(у1-у0). (
)=А(х1 – х0)+В(у1-у0). (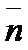 ;
; 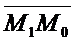 )=
)= 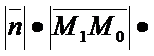 cos
cos 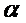 =
= 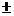
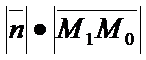 . А(х1 – х0)+В(у1-у0)=
. А(х1 – х0)+В(у1-у0)= 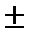
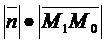 .
.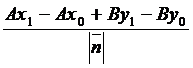 =
= 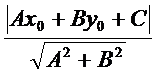 ------- формула для вычисления расстояния от точки до прямой, С=Ах1 +Ву1.
------- формула для вычисления расстояния от точки до прямой, С=Ах1 +Ву1.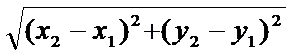 .
.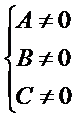
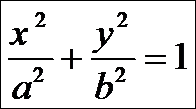 - Каноническое ур-е эллипса
- Каноническое ур-е эллипса

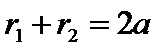 .
. 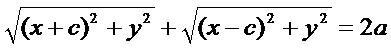 … b2=а2-с2
… b2=а2-с2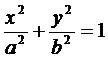 --каноническое уравнение, где a-большая полуось, b-меньшая полуось.
--каноническое уравнение, где a-большая полуось, b-меньшая полуось.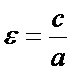 --- эксцентриситет эллипса. с2=а2-b2.
--- эксцентриситет эллипса. с2=а2-b2. 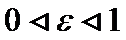 .
.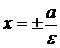 называются директрисами Э., параллельны Оу, лежат вне Э.
называются директрисами Э., параллельны Оу, лежат вне Э.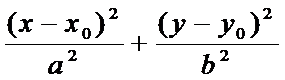 =1 также каноническое уравнение Э. с центром в т.(х0;у0).
=1 также каноническое уравнение Э. с центром в т.(х0;у0).
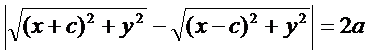
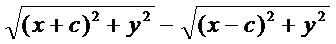 =
= 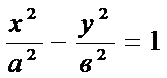 --- каноническое уравнение Г.
--- каноническое уравнение Г. Ур-я вида
Ур-я вида
 =
=  =
=  , b≠0.
, b≠0. - беск. большая и наоборот.В курсах матанализа док-ся, что П {Хn}=
- беск. большая и наоборот.В курсах матанализа док-ся, что П {Хn}= 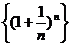 монот и огранич.По теореме: для того, чтобы монот сходилась, необхмо и достаточно, чтобы она была огранич. След-но, эта П имеет предел. Он обозначается буквой е: е=lim
монот и огранич.По теореме: для того, чтобы монот сходилась, необхмо и достаточно, чтобы она была огранич. След-но, эта П имеет предел. Он обозначается буквой е: е=lim  , причем е=2,718.
, причем е=2,718.


 ;
; 



 ;
;  ;
;
 2.
2. 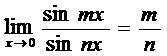








 , если
, если  , x
, x 
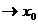


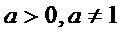 для любого х
для любого х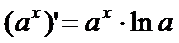
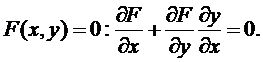 . Отсюда получим формулу для производной функции
. Отсюда получим формулу для производной функции 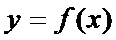 , заданной неявно:
, заданной неявно: 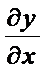 =
= 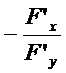 . Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением
. Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением 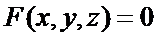 :
: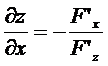 ,
, 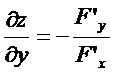 .
.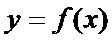 и пусть она: 1) опр-на и непрер на
и пусть она: 1) опр-на и непрер на 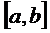 ; 2) имеет кон произв-ю
; 2) имеет кон произв-ю 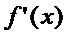 на
на 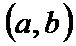 . Тогда найдётся такая т. с (a<c<b), что вып-ся рав-во
. Тогда найдётся такая т. с (a<c<b), что вып-ся рав-во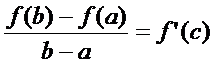 Док-во: Введём вспомогат функцию
Док-во: Введём вспомогат функцию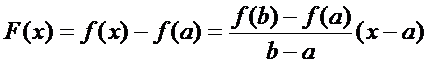
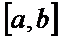 ,
, 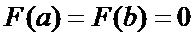 ,
,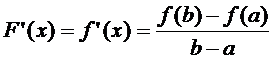 ,т.е. сущ на
,т.е. сущ на 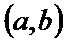 . След-но, найдётся точка с (a<c<b), такая, что F’(c) = 0, т.е.
. След-но, найдётся точка с (a<c<b), такая, что F’(c) = 0, т.е.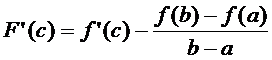 или
или 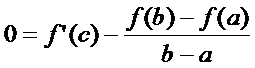
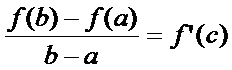 ∆
∆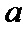 . Тогда при выч-и пределов
. Тогда при выч-и пределов 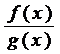 при x →
при x → 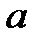 для раскрытия неопред-тей вида
для раскрытия неопред-тей вида  или
или 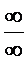 удобно применить пр. Лопиталя:
удобно применить пр. Лопиталя: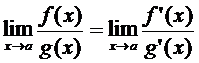 ,
, 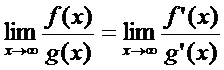 Неопределенности вида 0 · ∞, ∞ – ∞,
Неопределенности вида 0 · ∞, ∞ – ∞, 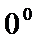 ,
, 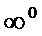 ,
, 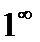 часто удается свести к неопределенностям вида
часто удается свести к неопределенностям вида 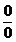 или
или  с помощью различных преобразований.
с помощью различных преобразований.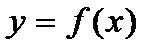 наз-ся возраст-ей на инт-ле
наз-ся возраст-ей на инт-ле 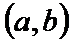 , если для любых
, если для любых 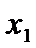 и
и 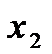 из этого инт-ла, для которых
из этого инт-ла, для которых 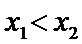 , верно нерав-во
, верно нерав-во 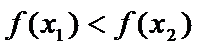 . Ф-я
. Ф-я 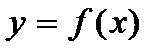 наз-ся убыв-ей на инт-ле
наз-ся убыв-ей на инт-ле 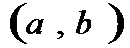 , если для любых x 1 и x 2 из этого инт-ла, для кот
, если для любых x 1 и x 2 из этого инт-ла, для кот 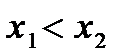 , верно нерав-во
, верно нерав-во 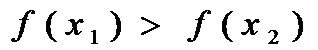 . Необх-ое усл-е возраст-я ф-ии:е сли ф-ия
. Необх-ое усл-е возраст-я ф-ии:е сли ф-ия 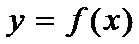 диффер-ма и возраста на инт-ле
диффер-ма и возраста на инт-ле 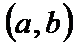 , то
, то 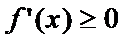 для всех х из этого инт-ла. Необх-ое усл-е убыв-я ф-ции. Если ф-ция
для всех х из этого инт-ла. Необх-ое усл-е убыв-я ф-ции. Если ф-ция 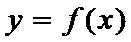 дифф-ма и убыва на инт-ле
дифф-ма и убыва на инт-ле 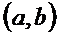 , то
, то 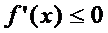 для всех х из этого инт-ла. Достаточное усл-е возраст-я (убыв-я ф-и). Пусть ф-я
для всех х из этого инт-ла. Достаточное усл-е возраст-я (убыв-я ф-и). Пусть ф-я 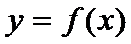 диф-ма на инт-ле
диф-ма на инт-ле 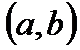 . Если во всех точках этого инт-ла
. Если во всех точках этого инт-ла 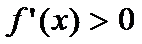 , то ф-ия возраста на этом интле, а если
, то ф-ия возраста на этом интле, а если 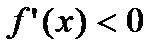 , то ф-я убывает на этом инт-ле.
, то ф-я убывает на этом инт-ле.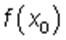 — максимумом функции, если для всех точек из некоторой окрестности точки x0, не совпадающих с x0, выполняется неравенство
— максимумом функции, если для всех точек из некоторой окрестности точки x0, не совпадающих с x0, выполняется неравенство 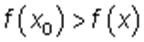 .
.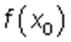 — минимумом функции, если для всех точек из некоторой окрестности точки x0, не совпадающих с точкой x0, выполняется неравенство
— минимумом функции, если для всех точек из некоторой окрестности точки x0, не совпадающих с точкой x0, выполняется неравенство 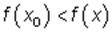 .
.

