| №№ п/п
| Функция
| Ряд Маклорена
| Интервал сходимости
|
| 1.
| 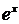
| 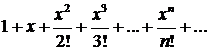
| 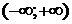
|
| 2.
| 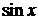
| 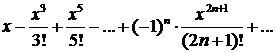
| 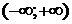
|
| 3.
| 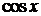
| 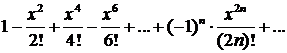
| 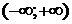
|
| 4.
| 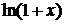
| 
| 
|
| 5.
| 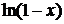
| 
| 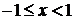
|
| 6.
| 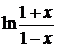
| 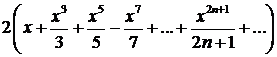
| 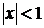
|
| Биномиальный ряд
|
| 7.
| 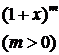
| 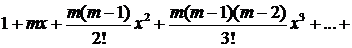
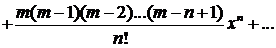
| 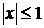
|
| 8.
| 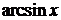
| 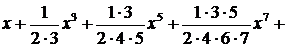
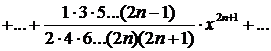
| 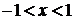
|
| 9.
| 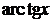
| 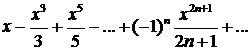
| 
|
12.5.5. ПРИМЕРЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ
С ПОМОЩЬЮ РЯДОВ
Пример 13. Вычислить значение  точностью до 0,001.
точностью до 0,001.
Решение. Ряд Маклорена для функции 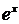 :
: 
сходится в интервале 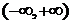 . Полагая
. Полагая 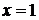 , получим:
, получим:
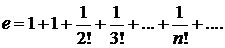
Для того чтобы выбрать необходимое число членов полученного числового ряда для вычисления значения е с заданной точностью, оценим остаток ряда  при
при 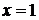 .
.
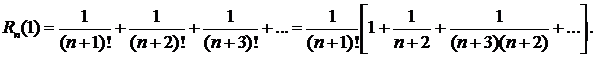
Заметим, что все члены последнего ряда не превышают значений соответствующих членов ряда
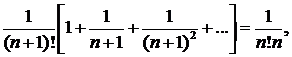
представляющего собой бесконечно убывающую геометрическую прогрессию. Следовательно, по теореме о сравнении знакоположительных рядов 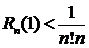 и ошибка, допускаемая при замене суммы ряда частичной суммой, не превосходит
и ошибка, допускаемая при замене суммы ряда частичной суммой, не превосходит 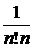 . Учтем, что при
. Учтем, что при  величина
величина  Значит, для вычисления
Значит, для вычисления  с точностью до 0,001 достаточно взять сумму первых пяти членов ряда:
с точностью до 0,001 достаточно взять сумму первых пяти членов ряда: 
Пример 14. Пользуясь соответствующим рядом, вычислить 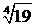 с точностью до 0,001.
с точностью до 0,001.
Решение. Выполним следующее преобразование:
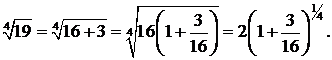
Применяя биномиальный ряд и полагая  ,
,  , получим:
, получим:

Учитывая, что в полученном знакочередующемся ряде значение четвертого члена меньше 0,001, делаем вывод: для вычисления 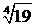 с заданной точностью достаточно взять сумму трех первых членов ряда:
с заданной точностью достаточно взять сумму трех первых членов ряда: 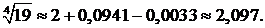
РЯДЫ ФУРЬЕ
Тригонометрический ряд  (1),
(1),
коэффициенты которого определяются формулами 


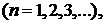 (2)
(2)
называется рядом Фурье, а числа 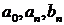 – коэффициентами Фурье функции
– коэффициентами Фурье функции  . Ряд Фурье, построенный для функции
. Ряд Фурье, построенный для функции  , обозначается так:
, обозначается так:
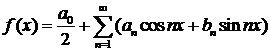 .
.
● Большое практическое значение имеет следующая задача: по заданной периодической функции  с периодом
с периодом  найти всюду сходящийся ряд (1), имеющий сумму
найти всюду сходящийся ряд (1), имеющий сумму  . Эта задача называется разложением данной функции
. Эта задача называется разложением данной функции  в ряд Фурье.
в ряд Фурье.
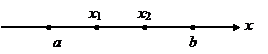 ● Если отрезок
● Если отрезок 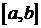 можно разбить внутренними точками
можно разбить внутренними точками  так, что на каждом из полученных промежутках
так, что на каждом из полученных промежутках  и
и 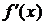 будут непре-
будут непре-
рывны и, кроме того, существуют конечные односторонние пределы  и
и
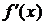 в концевых точках этих промежутков, то такая функция
в концевых точках этих промежутков, то такая функция  называется кусочно-дифференцируемой. Кусочно-дифференцируемая на отрезке
называется кусочно-дифференцируемой. Кусочно-дифференцируемая на отрезке 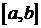 функция может быть на нем непрерывной или иметь конечное число точек разрыва первого ряда.
функция может быть на нем непрерывной или иметь конечное число точек разрыва первого ряда.
13.1. Достаточное условие разложения
функции в ряд Фурье
Если функция  кусочно-дифференцируема на отрезке
кусочно-дифференцируема на отрезке 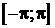 , то ее ряд Фурье сходится в каждой точке
, то ее ряд Фурье сходится в каждой точке 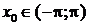 , и имеет сумму
, и имеет сумму
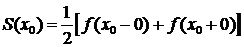 .
.
На концах отрезка сумма ряда Фурье определяется формулой:
 .
.
Кроме того, если 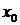 – точка непрерывности
– точка непрерывности  , то
, то
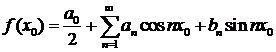 .
.
Пример 18. Разложить в ряд Фурье периодическую и заданную в интервале 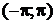 функцию
функцию 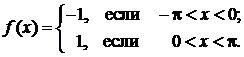 Построить график функции и второй частичной суммы
Построить график функции и второй частичной суммы  ее разложения в ряд Фурье.
ее разложения в ряд Фурье.
Решение. Данная функция имеет одну точку разрыва первого рода при 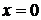 , а точки экстремума отсутствуют. Следовательно, данная функция удовлетворяет условиям Дирихле и может быть представлена рядом Фурье.
, а точки экстремума отсутствуют. Следовательно, данная функция удовлетворяет условиям Дирихле и может быть представлена рядом Фурье.
Интервал 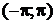 симметричен относительно начала координат и на этом интервале
симметричен относительно начала координат и на этом интервале 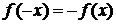 , следовательно, данная функция нечетная и ее ряд Фурье не содержит косинусов, так как коэффициенты Фурье
, следовательно, данная функция нечетная и ее ряд Фурье не содержит косинусов, так как коэффициенты Фурье 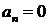 .
.
Найдем коэффициенты 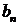 :
:
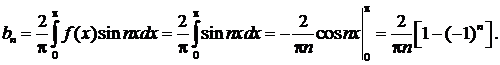
Разложение данной функции в ряд Фурье запишется следующим образом:

 Далее построим график данной функции (рис. 46, а).
Далее построим график данной функции (рис. 46, а).
Рис. 46, а
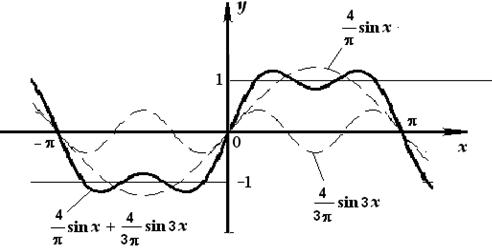
Для того чтобы выяснить, каким образом график функции приближается графиками последовательных частичных сумм полученного ряда, изобразим на рисунке графика самой функции последовательные гармоники ряда (пунктиром) и график 1-й и 2-й частичных сумм (рис. 46, б). Как видно из этого рисунка, чем больше последовательных гармоник ряда включает в себя частичная сумма, тем ближе график частичной суммы подходит к графику данной функции.
13.2. Ряд Фурье для функции, заданной на отрезке 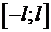
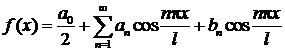 ,
,
где 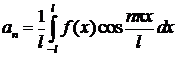
 ,
,

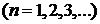 .
.
Замечание. Условия сходимости ряда Фурье для функции  , заданной на отрезке
, заданной на отрезке  аналогичны условиям разложения функции в ряд Фурье на отрезке
аналогичны условиям разложения функции в ряд Фурье на отрезке 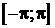 .
.
Пример 19. Разложить в ряд Фурье в указанном интервале функцию:

Решение. Вопрос о четности или нечетности данной функции не рассматриваем, так как она задана на интервале, не симметричном относительно начала координат. Длина указанного интервала (0,4) равна  . Определим коэффициенты Фурье для этой функции:
. Определим коэффициенты Фурье для этой функции:
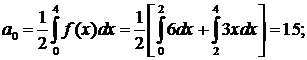
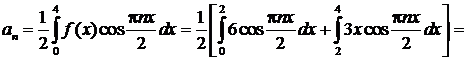
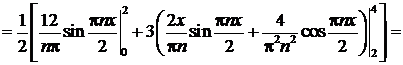
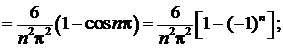



Ряд Фурье данной функции имеет вид:
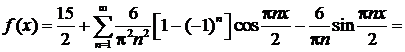
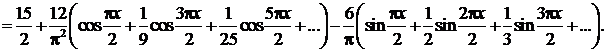
Полученное разложение справедливо во всей области определения заданной функции, причем в интервале (0,2) сумма ряда 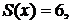 а в интервале (2,4) сумма ряда
а в интервале (2,4) сумма ряда 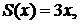 так как во всех точках непрерывности сумма ряда равна исходной функции. В точке разрыва
так как во всех точках непрерывности сумма ряда равна исходной функции. В точке разрыва 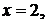 где функция не определена, сумма ряда
где функция не определена, сумма ряда 



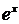
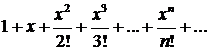
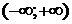
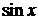
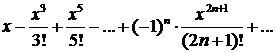
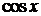
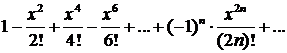
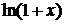


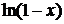

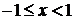
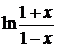
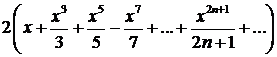
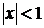
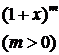
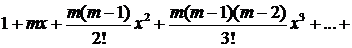
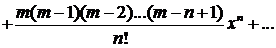
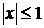
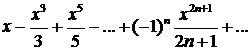
 точностью до 0,001.
точностью до 0,001.
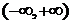 . Полагая
. Полагая 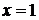 , получим:
, получим: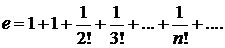
 при
при 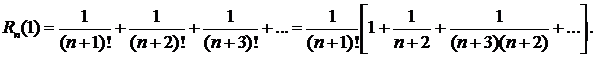
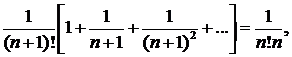
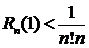 и ошибка, допускаемая при замене суммы ряда частичной суммой, не превосходит
и ошибка, допускаемая при замене суммы ряда частичной суммой, не превосходит 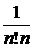 . Учтем, что при
. Учтем, что при  величина
величина  Значит, для вычисления
Значит, для вычисления 
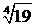 с точностью до 0,001.
с точностью до 0,001.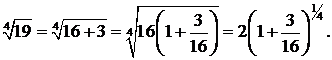
 ,
,  , получим:
, получим:
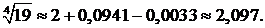
 (1),
(1),


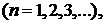 (2)
(2)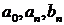 – коэффициентами Фурье функции
– коэффициентами Фурье функции  . Ряд Фурье, построенный для функции
. Ряд Фурье, построенный для функции 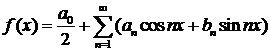 .
. найти всюду сходящийся ряд (1), имеющий сумму
найти всюду сходящийся ряд (1), имеющий сумму 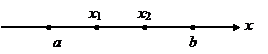 ● Если отрезок
● Если отрезок 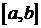 можно разбить внутренними точками
можно разбить внутренними точками  так, что на каждом из полученных промежутках
так, что на каждом из полученных промежутках 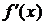 будут непре-
будут непре-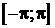 , то ее ряд Фурье сходится в каждой точке
, то ее ряд Фурье сходится в каждой точке 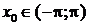 , и имеет сумму
, и имеет сумму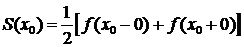 .
. .
.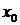 – точка непрерывности
– точка непрерывности 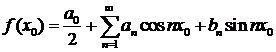 .
.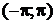 функцию
функцию 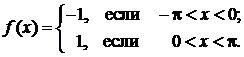 Построить график функции и второй частичной суммы
Построить график функции и второй частичной суммы  ее разложения в ряд Фурье.
ее разложения в ряд Фурье.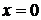 , а точки экстремума отсутствуют. Следовательно, данная функция удовлетворяет условиям Дирихле и может быть представлена рядом Фурье.
, а точки экстремума отсутствуют. Следовательно, данная функция удовлетворяет условиям Дирихле и может быть представлена рядом Фурье.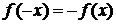 , следовательно, данная функция нечетная и ее ряд Фурье не содержит косинусов, так как коэффициенты Фурье
, следовательно, данная функция нечетная и ее ряд Фурье не содержит косинусов, так как коэффициенты Фурье 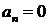 .
.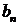 :
: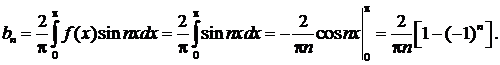

 Далее построим график данной функции (рис. 46, а).
Далее построим график данной функции (рис. 46, а).
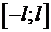
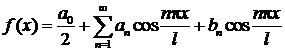 ,
,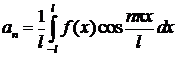
 ,
,
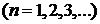 .
. аналогичны условиям разложения функции в ряд Фурье на отрезке
аналогичны условиям разложения функции в ряд Фурье на отрезке 
 . Определим коэффициенты Фурье для этой функции:
. Определим коэффициенты Фурье для этой функции: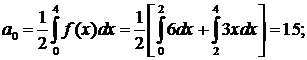
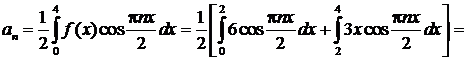
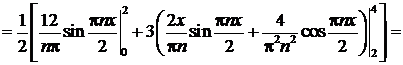
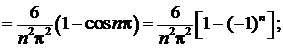



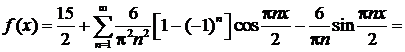
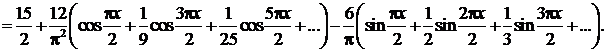
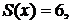 а в интервале (2,4) сумма ряда
а в интервале (2,4) сумма ряда 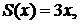 так как во всех точках непрерывности сумма ряда равна исходной функции. В точке разрыва
так как во всех точках непрерывности сумма ряда равна исходной функции. В точке разрыва 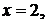 где функция не определена, сумма ряда
где функция не определена, сумма ряда 



