● Полем называется часть пространства, каждой точке которого поставлено в соответствие определенное значение некоторой физической величины. Если физическая величина скалярная, то поле называется скалярным, а если векторная, то – векторным.
Скалярное поле считается заданным, если в каждой его точке Р определена скалярная функция 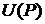 , называемая функцией поля. Примерами скалярных полей могут служить поле распространения температуры, поле потенциала в электрическом поле и т. д. Поле называется стационарным, если величина
, называемая функцией поля. Примерами скалярных полей могут служить поле распространения температуры, поле потенциала в электрическом поле и т. д. Поле называется стационарным, если величина 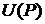 не зависит от времени.
не зависит от времени.
● Поверхностью уровня скалярного поля называется геометрическое множество точек, в которых функция 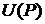 принимает постоянное значение, т. е.
принимает постоянное значение, т. е.  .
.
В частности, если скалярное поле плоское, то функция поля U зависит от двух переменных х и у. В этом случае рассматривают линию уровня. Линией уровня функции  называется такая линия на плоскости
называется такая линия на плоскости 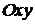 , в точках которой функция сохраняет постоянное значение, т. е. уравнение
, в точках которой функция сохраняет постоянное значение, т. е. уравнение  определяет линии уровня.
определяет линии уровня.
● Пусть задана функция поля 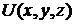 . Рассмотрим какой-нибудь луч l, выходящий из произвольной точки
. Рассмотрим какой-нибудь луч l, выходящий из произвольной точки  . Направление этого
. Направление этого
луча зададим углами α, β, γ, которые он образует с положительными направлениями осей координат. Если l 0 – единичный вектор, направлен-
ный по лучу l, то его проекциями будут направляющие косинусы:  . Пусть точка
. Пусть точка 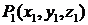 лежит на луче l. Расстояние
лежит на луче l. Расстояние  обозначим через ρ. Тогда предел отношения изменения функции
обозначим через ρ. Тогда предел отношения изменения функции 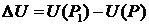 к изменению величины ρ, при условии
к изменению величины ρ, при условии 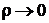 называется производной от функции
называется производной от функции 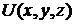 по направлению l в точке Р и обозначается
по направлению l в точке Р и обозначается  .
.
Теорема. Для всякой дифференцируемой функции 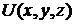 существует производная
существует производная  по любому направлению
по любому направлению  , такая что
, такая что
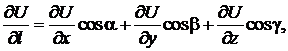
где cosα, cosβ, cosγ – направляющие косинусы направления l.
Абсолютная величина производной  определяет величину скорости, а знак производной – характер изменения функции U (возрастание или убывание) в точке Р по направлению луча l. Среди всех направлений можно выделить такое, по которому скорость изменения функции
определяет величину скорости, а знак производной – характер изменения функции U (возрастание или убывание) в точке Р по направлению луча l. Среди всех направлений можно выделить такое, по которому скорость изменения функции 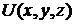 будет наибольшей. Это направление задается вектором, который называют градиентом функции U в точке Р и обозначается
будет наибольшей. Это направление задается вектором, который называют градиентом функции U в точке Р и обозначается 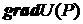 или
или  .
.
Итак,  . Модуль градиента
. Модуль градиента 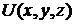 в точке Р равен наибольшей скорости изменения скалярного поля:
в точке Р равен наибольшей скорости изменения скалярного поля: 
Таким образом, каждой точке скалярного поля соответствует определенный вектор – градиент функции 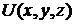 , характеризующий наибольшую скорость изменения этой функции.
, характеризующий наибольшую скорость изменения этой функции.
Можно показать, что  в каждой точке совпадает с нормалью к поверхности уровня скалярного поля, проходящей через эту точку. Таким образом, градиент в каждой точке перпендикулярен касательной плоскости к поверхности уровня, проходящей через данную точку, значит, его проекция на эту плоскость равна нулю. Следовательно, производная по направлению, касательному к поверхности уровня, проходящей через данную точку, равна нулю.
в каждой точке совпадает с нормалью к поверхности уровня скалярного поля, проходящей через эту точку. Таким образом, градиент в каждой точке перпендикулярен касательной плоскости к поверхности уровня, проходящей через данную точку, значит, его проекция на эту плоскость равна нулю. Следовательно, производная по направлению, касательному к поверхности уровня, проходящей через данную точку, равна нулю.
Векторное поле
● Векторным полем называется часть пространства, в каждой точке которого задана векторная величина (силовое поле, поле скоростей текущей жидкости и др.).
Пусть векторное поле образовано вектором
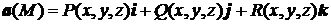
● Потоком вектора а через поверхность σ называется поверхно-стный интеграл вида 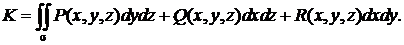
В случае, когда векторное поле 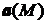 представляет поле скоростей текущей жидкости, то величина потока K определяет количество жидкости, протекающее через поверхность σ.
представляет поле скоростей текущей жидкости, то величина потока K определяет количество жидкости, протекающее через поверхность σ.
● Дивергенция или расходимость векторного поля а в любой его точке М выражается формулой:
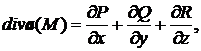
где значения частных производных берутся в точке М.
● Теорема Остроградского–Гаусса
Поток вектора а изнутри замкнутой поверхности σ равен тройному интегралу по объему V, ограниченному этой поверхностью, от дивергенции векторного поля: 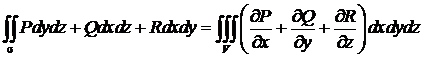
● Работа в силовом поле 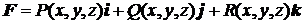 вдоль кривой
вдоль кривой 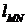 находится с помощью криволинейного интеграла по формуле
находится с помощью криволинейного интеграла по формуле
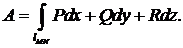
Если l замкнутый контур, то криволинейный интеграл 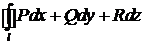 называется циркуляцией.
называется циркуляцией.
● Ротором (вихревым вектором) векторного поля 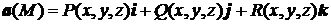 называется вектор
называется вектор
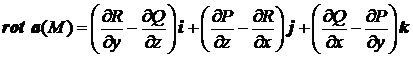 .
.
Замечание. Удобно координаты вектора 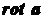 находить с помощью специального определителя:
находить с помощью специального определителя: 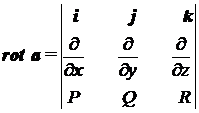
● Теорема Стокса
Поток ротора поля через поверхность σ равен циркуляции вектора по границе l этой поверхности.
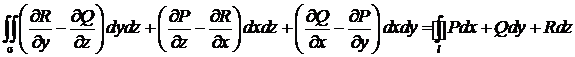 .
.
Замечание. Направление интегрирования по контуру l и направление нормали n к поверхности σ согласованы так, что с конца нормали n обход вдоль контура l виден против хода часовой стрелки.



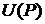 , называемая функцией поля. Примерами скалярных полей могут служить поле распространения температуры, поле потенциала в электрическом поле и т. д. Поле называется стационарным, если величина
, называемая функцией поля. Примерами скалярных полей могут служить поле распространения температуры, поле потенциала в электрическом поле и т. д. Поле называется стационарным, если величина  .
. называется такая линия на плоскости
называется такая линия на плоскости 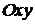 , в точках которой функция сохраняет постоянное значение, т. е. уравнение
, в точках которой функция сохраняет постоянное значение, т. е. уравнение  определяет линии уровня.
определяет линии уровня.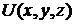 . Рассмотрим какой-нибудь луч l, выходящий из произвольной точки
. Рассмотрим какой-нибудь луч l, выходящий из произвольной точки  . Направление этого
. Направление этого  . Пусть точка
. Пусть точка 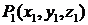 лежит на луче l. Расстояние
лежит на луче l. Расстояние  обозначим через ρ. Тогда предел отношения изменения функции
обозначим через ρ. Тогда предел отношения изменения функции 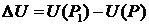 к изменению величины ρ, при условии
к изменению величины ρ, при условии 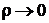 называется производной от функции
называется производной от функции  .
. , такая что
, такая что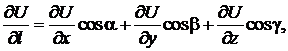
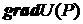 или
или  .
. . Модуль градиента
. Модуль градиента 
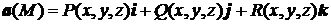
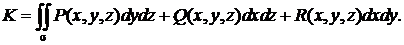
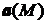 представляет поле скоростей текущей жидкости, то величина потока K определяет количество жидкости, протекающее через поверхность σ.
представляет поле скоростей текущей жидкости, то величина потока K определяет количество жидкости, протекающее через поверхность σ.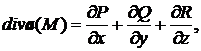
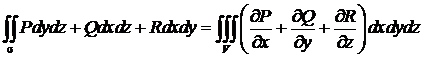
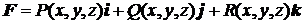 вдоль кривой
вдоль кривой 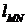 находится с помощью криволинейного интеграла по формуле
находится с помощью криволинейного интеграла по формуле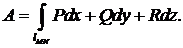
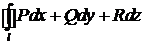 называется циркуляцией.
называется циркуляцией.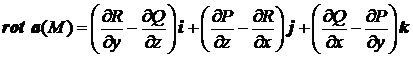 .
.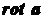 находить с помощью специального определителя:
находить с помощью специального определителя: 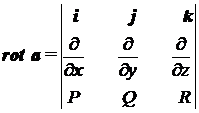
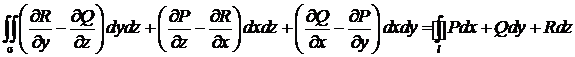 .
.


