Прямоугольная проекция окружности

При выполнении машиностроительных чертежей часто возникает необходимость построения прямоугольных проекций окружности.

Если окружность лежит в плоскости уровня, то, естественно, она проецируется на одну из плоскостей проекций в натуральную величину, а на другую плоскость проекций - в отрезок, совпадающий с вырожденной проекцией плоскости.

Рис.8.5

Если окружность лежит в проецирующей плоскости, то одна ее проекция вырождается в отрезок, равный диаметру заданной окружности, и совпадает с вырожденной плоскостью, вторая проекция - эллипс (рис. 8.5).. Построение проекции окружности l, заданного диаметра d, лежащей во фронтально проецирующей плоскости, расположенной под углом 45° к П₁ ясно из чертежа.

На П₂ отрезок С₂D₂ равен d. На П₁ эллипс l₁ строим известным способом с помощью окружностей радиусами малой и большой полуоси эллипса, делением окружностей диаметральными линиями и получением точек Мⁱ.

Окружность, лежащая в плоскости общего положения, проецируется на обе плоскости проекций в эллипсы.

Рис.8.6

Пример. Построить проекции l₁, l₂ окружности l(О,R), лежащей в плоскости q(hÇf), где О=hÇf (рис. 8.6).

Отметим, что большие оси эллипсов l₁,l₂ принадлежат линиям уровня, соответственно горизонтали h и фронтали f и по величине равны диаметру окружности l. Поэтому большую ось А₁В₁ эллипса l₁ на П₁ откладываем на горизонтальной проекции горизонтали h₁, а большую ось М₂N₂ эллипса l₂ - на фронтальной проекции фронтали f₂. Вторые проекции А₂В₂, М₁,N₁ находим из условий принадлежности соответственно точек А,В,М,N горизонтали и фронтали.

Для построения малых осей С₁Д₁ и Р₂Q₂ проводим прямые n₁^А₁В₁, m₂^М₂N₂. Эллипс l₁ теперь определен большой осью А₁В₁, направлением n₁ малой оси и двумя точками М₁,N₁. Этих условий достаточно для графического определения величины его малой оси:

¨ через точку М₁ искомого эллипса l₁ проводим прямые, параллельные А₁В₁ и n₁;

¨ отмечаем точку 2 пересечения прямой, параллельной n₁, с окружностью u, описанной на А₁В₁, как на диаметре;

¨ отмечаем точку 1=0₁2ÇМ₁1 и получаем отрезок 0₁1, определяющий величину малой полуоси эллипса l₁.

Аналогично определяется величина малой полуоси эллипса l₂ - фронтальной проекции окружности l.

Обводы

Решение ряда задач требует построения линий, проходящих через упорядоченный массив точек или через данные точки и имеющие в них наперед заданные положения касательных, кругов кривизны и т.д. Иногда требуется какую-либо графически или аналитически заданную кривую заменить другой кривой.

Если исходная кривая задана большим числом точек, то выбор новой кривой, качественно заменяющей исходную, требует выполнения сложных вычислений. Для упрощения решения задачи в качестве заменяющей линии конструируют составную кривую - обвод.

Обводом называется линия, составленная из дуг кривых выбранного вида, которые в стыковых точках имеют определенный порядок соприкосновения.

В инженерной практике в качестве составляющих обводов обычно используют отрезки прямых, дуги кривых второго и третьего порядка. Порядок составляющих в стыковых точках определяет порядок гладкости обвода. Если смежные составляющие имеют в стыковых точках общие касательные, то составная линия называется обводом первого порядка гладкости. Составная линия представляет собой обвод второго порядка гладкости, если график изменения кривизны по ее длине будет непрерывным.

Рассмотрим один из способов построения обводов - радиусографический.

Пример. Через упорядоченный массив точек Аⁱ(i=1,2...,n) необходимо провести обвод первого порядка гладкости, составленный из дуг окружностей (рис. 8.7).

Рис.8.7

Построение составляющих обвода основано на простых свойствах окружностей при построении их сопряжений. Первая составляющая m¹ однозначно определяется первыми тремя точками А¹,А²,А³. Центр О¹ дуги m¹ строится как точка пересечения перпендикуляров р¹,р², восстановленных из середин С¹,С² ее хорд - А¹А², А²А³.

Вторая и последующие составляющие m², m³ определяются двумя точками и касательной, построенной к предыдущей составляющей в стыковой точке. Центр О² второй составляющей m² определяется как точка пересечения прямой О¹А³, соединяющей центр О¹ предыдущей окружности со стыковой точкой А³, с перпендикуляром р³, восстановленным из середины С³ хорды А³А⁴. Аналогично строится все последующие составляющие m^j(j=1,2,...n-2).

Вопросы для самопроверки к лекции 8:

1. Как принято рассматривать кривую линию в начертательной геометрии?

2. Назовите основные понятия, характеризующие кривую линию.

3. Назовите проекционные свойства кривых линий.

4. Как может проецироваться окружность на плоскости проекций?

5. Что называется обводом?

 

ЛЕКЦИЯ 9

 

ПОВЕРХНОСТИ

Поверхности составляют обширное многообразие нелинейных фигур трехмерного пространства. Любое тело ограничивается своей поверхностью. Нет ни одной области деятельности человека, где бы он не сталкивался с поверхностями в виде материальных, физических моделей.

Инженерная деятельность связана непосредственно с конструированием, расчетом, изготовлением различных технических поверхностей. Большинство задач прикладной геометрии сводится к автоматизации конструирования, расчету и воспроизведению сложных технических поверхностей.

 

9.1. Основные понятия и определения

В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая в декартовой системе координат уравнением вида F(x,y,z)=0, где F(x,y,z) -многочлен n-й степени, или в форме какой либо трансцендентной функции. В первом случае поверхности называют алгебраическими, во втором - трансцендентными.

Если алгебраическая поверхность описывается уравнением n -й степени, то поверхность считается n-го порядка. Любая произвольно расположенная плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет сама поверхность. Порядок поверхности может быть определен также числом точек ее пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).

Рис.9.1

В начертательной геометрии геометрические фигуры задаются графически, поэтому поверхность целесообразно рассматривать кинематически: как совокупность всех последовательных положений некоторой перемещающейся в пространстве линии. Образование поверхности с помощью линии позволяет дать иное определение поверхности, базирующееся на основных элементарных геометрических понятиях, таких как точка и множество. Действительно, если принять, что положение движущейся в пространстве линии будет непрерывно меняться с течением времени t, и принять t за параметр, то поверхность можно рассматривать как непрерывное однопараметрическое множество линий. В свою очередь, линия определяется как непрерывное однопараметрическое множество точек, поэтому можно дать следующее определение поверхности: поверхностью называется непрерывное двухпараметрическое множество точек.

Изображение по-верхности на плоскости проекций получают обычно заданием перемещающейся l и направляющей линий m с указанием характера перемещения подвижной линии (рис. 9.1.) Перемещающаяся линия называется образующей. Характер перемещения образующей может быть определен, например, с помощью проецирующей плоскости S.

Процесс образования и изображения показанной поверхности можно записать так:

1. l₁||S;

2. l_i'AÎm,

l_i'A¢Îm¢.

Эти условия сохраняются и на проекции поля П₁.

Другим способом образования и задания поверхности на чертеже является изображение поверхности множеством принадлежащих ей точек или линий, которые выбирают так, чтобы они давали возможность с достаточной степенью точности определять форму поверхности и решать на ней различные задачи (рис. 9.2).

Рис.9.2

Упорядоченное множество точек или линий, принадлежащих поверхности, называется ее каркасом. В зависимости от того, чем задается каркас поверхности, точками или линиями каркасы подразделяются на точечные и линейчатые.

Линейчатый каркас считается непрерывным, если его параметр выражается непрерывной функцией, в противном случае он называется дискретным.

Поверхность будет задана (определена), если в любой момент движения образующей будут известны ее положение и форма, а это в свою очередь позволяет однозначно отвечать на вопрос положения точки на данной поверхности.

Кинематический способ образования поверхности подводит нас к понятию определителя, под которым мы будем подразумевать необходимую и достаточную совокупность геометрических элементов и связей между ними, которые однозначно определяют поверхность.

В определитель должны быть включены:

1. Геометрическая часть, определяющая перечень геометрических элементов, участвующих в образовании поверхности.

2. Алгоритмическая часть, указывающая на взаимосвязь между геометрическими элементами.

Итак, определитель поверхности состоит из двух частей: из совокупности геометрических элементов (1-я часть) и дополнительных сведений (2-ая часть).

В общем случае определитель будет иметь следующую структурную форму:

Ф (Г) [А], где (Г) - геометрическая часть,

[А] - алгоритмическая часть.

Для определения конкретного вида поверхности в каждую часть определителя вкладывается конкретное содержание.

Классификация поверхностей

Многообразие поверхностей требует их систематизации. При рассмотрении кинематического образования поверхностей в основе систематизации лежат два признака: вид образующей и закон ее перемещения. По виду образующей принято различать линейчатые (образующая-прямая), циклическая (образующая-окружность) и поверхности зависимых сечений (образующая - плоская кривая), по закону перемещения образующей - поверхности параллельного переноса, вращения и винтовые.

Такая систематизация является достаточно условной, ибо одна и та же поверхность может быть отнесена одновременно к различным видам. Например, коническая поверхность вращения относится к линейчатым и поверхностям вращения. Или любую перечисленную группу поверхностей можно считать поверхностями зависимых сечений, так как, пересекая их семейством плоскостей, получаем множество плоских сечений, характеристики которых взаимозависимы.

Линейчатые поверхности

Рис.9.3

Как было показано ранее, это поверхности, которые образованы движением в пространстве прямой линии.

Линейчатая поверхность в общем случае однозначно определяется тремя направляющими.

Действительно, пусть даны три пространственные кривые линии m,n и l (рис. 9.3), Возьмем на кривой m произвольную точку М, примем ее за вершину конической поверхности q, а за направляющую этой поверхности возьмем кривую l. Если N точка пересечения кривой n с поверхностью q, то МN пересекает кривую l в точке L. Это не вызывает сомнений, так как и МN и кривая l принадлежат одной и той же поверхности q. Из чертежа видно, что через точку М, взятую на одной из направляющих, проходит одна и только одна прямолинейная образующая а, пересекающая две другие направляющие n и l. Задавая другое положение точке М®M¢(M¢Îm) и принимая ее за вершину конической поверхности, мы получим при той же направляющей l, новую коническую поверхность q¢, которая пересекается кривой n в точке N¢. Точки M¢ и N¢ определяют положение прямой а¢, которая пересекает третью направляющую l в точке L¢. а¢ - новая образующая линейчатой поверхности.

Описанным способом можно построить любое число прямолинейных образующих, которые выделят в пространстве одну единственную линейчатую поверхность.

Так как положение прямолинейных образующих однозначно определяется формой и положением в пространстве направляющих m,n и l, то в общем виде определитель линейчатой поверхности может быть задан тремя направляющими и словесным добавлением, что поверхность линейчатая, и записью обозначится так: Ф(m,n,l).

В зависимости от формы направляющих и их расположения в пространстве, получаем разнообразные поверхности этой группы, которые могут быть отнесены к четырем видам:

1. Поверхность косого цилиндра с тремя направляющими подобранными соответствующим образом;

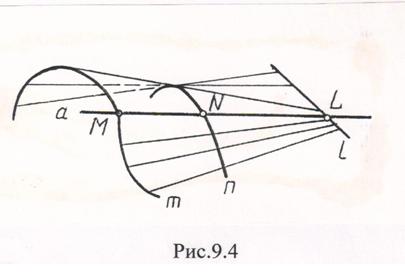
2. Поверхность дважды косого цилиндра. Направляющие - две кривые и прямая (рис.9.4). Направляющие в этом случае лежат в параллельных плоскостях.

3. Поверхность дважды косого коноида. Две направляющие m и l скрещивающиеся прямые, а n- кривая.

Рис.9.4

4. Поверхность однополостного гиперболоида. Эта поверхность получается при движении прямой а по трем скрещивающимся прямым m, n и l.