Гомоскедастичность - это предположение оттом, что дисперсии случайной ошибки 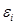 является известной постоянной величиной для всех
является известной постоянной величиной для всех 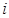 наблюдений регрессионной модели.
наблюдений регрессионной модели.
Гетероскедастичность - означает предположение о дисперсии случайных ошибок регрессионной модели.
Существует несколько способов на обнаружение гетероскедастичности в регрессионной модели:
1) Тест Глейзера. Строится обычная регрессионная модель: 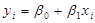 Методом наименьших квадратов вычисляются оценки коэффициентов построенной модели:
Методом наименьших квадратов вычисляются оценки коэффициентов построенной модели:  . Затем вычисляются остатки регрессионной модели:
. Затем вычисляются остатки регрессионной модели: 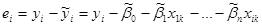 . Полученные регрессионные остатки возводятся в квадрат
. Полученные регрессионные остатки возводятся в квадрат  .
.
2) Тест Голдфелда – Квандта - состоит в следующем:
· Все n наблюдений упорядочиваются по величине xj.
· Вся упорядоченная выборка разбивается на три подвыборки размерностей k, n-2k и k соответственно.
· Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений).
· Для сравнения соответствующих дисперсий выдвигается нуль – гипотеза в виде

которая предполагает отсутствие гетероскедастичности. Для проверки нуль – гипотезы строится следующая статистика
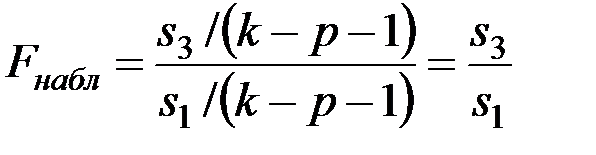
которая при справедливости нуль – гипотезы имеет распределение Фишера с (k-p-1, k-p-1) степенями свободы.
· Если
 ,
,
то гипотеза об отсутствии гетероскедастичности отклоняется на уровне значимости α.
3) Для обнаружения гетероскедастичности определяется коэффициент Спирмена. Коэффициент Спирмена является аналогом парного коэффициента корреляции, но позволяет выявить взаимосвязь между качественным и количественным признаками:  ,
,
где d - ранговая разность ( -
-  );
);
n - количество пар вариантов.
Критическое значение определяется по таблице распределения Стьюдента:  . Если
. Если 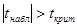 , то между переменной
, то между переменной  и остатками регрессионной модели
и остатками регрессионной модели  присутствует гетероскедастичность.
присутствует гетероскедастичность.
33. Суть ANOVA-моделей и ANCOVA-моделей.
ANOVA-модели - Регрессионные модели, содержащие лишь качественные объясняющие переменные. Например, зависимость начальной заработной платы от образования может быть записана так:

где D=0, если претендент на рабочее место не имеет высшего образования,
D=1, если имеет.
Тогда при отсутствии высшего образования начальная заработная плата равна:  а при его наличии:
а при его наличии: 
При этом параметр а определяет среднюю начальную заработную плату при отсутствии высшего образования. Коэффициент g показывает, на какую величину отличаются средние начальные заработные платы при наличии и при отсутствии высшего образования у претендента. Проверяя статистическую значимость коэффициента g с помощью t – статистики, можно определить, влияет или нет наличие высшего образования на начальную заработную плату. Нетрудно заметить, что ANOVA – модели представляют собой кусочно –постоянные функции. Такие модели в экономике крайне редки. Гораздо чаще встречаются модели, содержащие как количественные, так и качественные переменные.
ANCOVA-модели - Регрессионные модели, в которых объясняющие переменные носят как количественный, так и качественный характер.






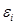 является известной постоянной величиной для всех
является известной постоянной величиной для всех 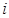 наблюдений регрессионной модели.
наблюдений регрессионной модели.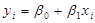 Методом наименьших квадратов вычисляются оценки коэффициентов построенной модели:
Методом наименьших квадратов вычисляются оценки коэффициентов построенной модели:  . Затем вычисляются остатки регрессионной модели:
. Затем вычисляются остатки регрессионной модели: 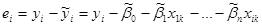 . Полученные регрессионные остатки возводятся в квадрат
. Полученные регрессионные остатки возводятся в квадрат  .
.
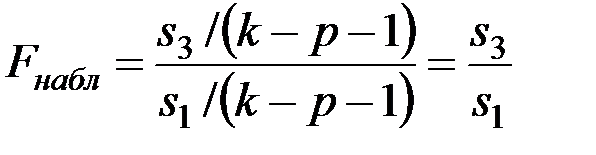
 ,
, ,
, -
-  );
); . Если
. Если 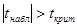 , то между переменной
, то между переменной  и остатками регрессионной модели
и остатками регрессионной модели  присутствует гетероскедастичность.
присутствует гетероскедастичность.
 а при его наличии:
а при его наличии: 



