МАТЕМАТИКА (ТЕОРИЯ)
Профиль – начальное образование)
Пояснительная записка
Данный УМК разработан для студентов – заочников направления «Педагогическое образование» по профилю «Начальное образование». По учебному плану на изучение «Математики» выделено всего 14 аудиторных часов, в течение которых преподавателю необходимо ознакомить студентов с теоретическими основами курса математики начального образования.
Запланированных 4 часов лекционных занятий достаточно только для краткого ознакомления с задачами изучения курса, рекомендации списка учебной литературы.
Анализ многих программ по математике, предлагаемых для изучения учащимся начальной школы, показывает, что учитель, работающий в школе или готовится к этой работе, должен иметь как достаточно серьезную теоретическую подготовку, так и обладать развитым математическим и логическим мышлением. В связи с этим в подготовку бакалавра – будущего учителя начального образования – целесообразно включить не только изучение фактического содержания курса математики начального образования (множеств, натуральных чисел, делимости чисел, систем счисления, простейших понятий функции и уравнения), но и некоторые сведения методологического характера - элементов математической логики, методов определения математического понятия, аксиоматического метода построения теории и др.
В дополнение к существующей учебной литературе для подготовки учителя начального образования по математике автор разработанного УМК предлагает необходимый, на его взгляд, теоретический материал по дисциплине «Математика».
Предложенный курс разбит на темы, в процессе изложения содержания тем выделены отдельные пункты, не предполагается никаких почасовых ограничений, материал предназначен в основном, для самостоятельного изучения курса математики.
ТЕМА I - МНОЖЕСТВА
Понятие множества, геометрическая интерпретация числовых множеств на числовой прямой
Операции с числовыми множествами (объединение, пересечение, разность).
Декартово произведение множеств
ТЕМА II – ЭЛЕМЕНТЫ МАТЕМАТИЧЕКСОЙ ЛОГИКИ
1. Понятие высказывания, логической операции с высказываниями.
Операции отрицания, конъюнкции, дизъюнкции, импликации,
Эквиваленции.
Свойства логических операций.
Понятие предиката с одной переменной.
Операции отрицания, конъюнкции, дизъюнкции, импликации,
Эквиваленции
(а) Логической операции «отрицание высказываний» соответствует логическая связка «не». Если высказывание А – истинно (т.е. А=1), то, утверждая, что А ложно, получаем новое высказывание, отрицание А, обозначается  . При этом, если А=1, то
. При этом, если А=1, то  =0, если А=0, то
=0, если А=0, то  =1. Отрицание высказывания часто строится при помощи слова «неверно».Например, пусть А:
=1. Отрицание высказывания часто строится при помощи слова «неверно».Например, пусть А:
«Санкт – Петербург расположен на Неве» (А=1), тогда  : «неверно что Санкт – Петербург расположен на Неве», или «Санкт – Петербург не расположен на Неве» (
: «неверно что Санкт – Петербург расположен на Неве», или «Санкт – Петербург не расположен на Неве» ( =0). Все значения заданных и полученных высказываний сводятся в одну таблицу, таблицу истинности, которая позволяет ввести формальное определение операции.
=0). Все значения заданных и полученных высказываний сводятся в одну таблицу, таблицу истинности, которая позволяет ввести формальное определение операции.
Опр.2. Отрицанием высказывания А называется новое высказывание  (неверно, что А), истинность которого задается таблицей (табл 1)
(неверно, что А), истинность которого задается таблицей (табл 1)
| А
| 
|
|
|
|
|
|
|
Табл 1
(б) Логической операции «конъюнкция» соответствует логическая связка «и», ее символ -  , A
, A  B – обозначение конъюнкции высказываний А и В.
B – обозначение конъюнкции высказываний А и В.
Опр.3. Конъюнкцией двух высказываний А и В называется новое высказывание С=A  B, полученное соединением этих высказываний посредством связки «и» (
B, полученное соединением этих высказываний посредством связки «и» ( ), истинность которого определяется таблицей (Табл 2):
), истинность которого определяется таблицей (Табл 2):
| А
| В
| A  B B
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Табл 2
Таблица показывает, что конъюнкция истинна только тогда, когда истинны оба высказывания, в остальных случая конъюнкция ложна.
Пример 1. Пусть имеем два высказывания А и В.
А: 5<10, А=1;
В: 10<16, В=1; тогда конъюнкция A  B записывается:
B записывается:
A  B: (5<10)
B: (5<10)  (10<16), или 5<10<16, при этом полученное неравенство истинно, A
(10<16), или 5<10<16, при этом полученное неравенство истинно, A  B=1 - имеем истинное двойное неравенство. Иначе говоря, двойное числовое неравенство вида a<b<c является конъюнкцией двух неравенств: a<b и b<c.
B=1 - имеем истинное двойное неравенство. Иначе говоря, двойное числовое неравенство вида a<b<c является конъюнкцией двух неравенств: a<b и b<c.
Пример 2. Пусть имеем два высказывания А и В.
А: 7-2=5, А=1; В: 8 – число четное, В=1, конъюнкция A  B записывается:
B записывается:
A  B: (7-2=5)
B: (7-2=5)  (8 – число четное). По составленной таблице, конъюнкция двух истинных высказываний есть высказывание истинное.
(8 – число четное). По составленной таблице, конъюнкция двух истинных высказываний есть высказывание истинное.
Замечание 1: Последний пример показывает, что при построении логических операций содержательная сторона высказываний не всегда имеет значение.
(в) Логической операции «дизъюнкция» соответствует логическая связка «или», ее символ -  , A
, A  B – обозначение дизъюнкции высказываний А и В.
B – обозначение дизъюнкции высказываний А и В.
Опр. 4. Дизъюнкцией двух высказываний А и В называется новое высказывание С= A  B, полученное соединением этих высказываний посредством связки «или» (
B, полученное соединением этих высказываний посредством связки «или» ( ), истинность которого определяется таблицей (Табл 3)
), истинность которого определяется таблицей (Табл 3)
| A
| B
| A  B B
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Табл 3
Таблица показывает, что дизъюнкция истинна всегда, кроме случая ложности обоих высказываний.
Пример 3. Пусть имеем два высказывания А и В.
А: 5<10, А=1;
В: 5=10, В=0; тогда конъюнкция A  B записывается:
B записывается:
A  B: (5<10)
B: (5<10)  (5=10), эту дизъюнкцию можно записать в виде
(5=10), эту дизъюнкцию можно записать в виде  , причем, по таблице - A
, причем, по таблице - A  B=1. Иначе, нестрогое числовое неравенство вида
B=1. Иначе, нестрогое числовое неравенство вида  является дизъюнкцией строгого неравенства
является дизъюнкцией строгого неравенства  и равенства
и равенства  .
.
Пример 4. Пусть имеем два высказывания А и В.
А: 2=3, А=0;
В: 2>3, В=0, по таблице истинности дизъюнкция A  B:
B:
(2=3)  (2>3) – ложна, как дизъюнкция двух ложных высказываний.
(2>3) – ложна, как дизъюнкция двух ложных высказываний.
(г) Логической операции «импликация» соответствует логическая связка «если…то»,ее символ -  , A
, A  B – обозначение импликации высказываний А и В.
B – обозначение импликации высказываний А и В.
Опр.5. Импликацией двух высказываний А и В называется новое высказывание С=(A  B), полученное соединением этих высказываний посредством связки «если…то» (
B), полученное соединением этих высказываний посредством связки «если…то» ( ), истинность которого определяется таблицей (Табл 4)
), истинность которого определяется таблицей (Табл 4)
| A
| B
| A  B B
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Табл 4
Таблица показывает, что импликация истинна всегда, кроме значения 0 в строке в которой имеется число 100.
Символическая запись «A  В» читается:
В» читается:
- из А следует В;
- если А, то В.
Замечание 2: В обыденной жизни под выражением «если А, то В» обычно подразумевается тот факт, что если произойдет событие А, то произойдет и событие В. В математической логике это не всегда так. Для двух высказываний А (А: 10:5=2) и В (В: на улице холодно) можно построить импликацию «A  В» ( если 10:5=2, то на улице холодно). Истинность таких импликаций проверяется по таблицам истинности, однако с точки зрения здравого смысла такая импликация не имеет смысла.
В» ( если 10:5=2, то на улице холодно). Истинность таких импликаций проверяется по таблицам истинности, однако с точки зрения здравого смысла такая импликация не имеет смысла.
Замечание 3: в изучении логических законов при введении для рассмотрения нового объекта А часто используется выражение «для любого А», для краткости это выражение записывается символически « А». Смысл этого символа рассмотрим позже.
А». Смысл этого символа рассмотрим позже.
Рассмотрим случай применения понятия импликации в курсе математики.
Пусть А: «Четырехугольник MNPQ – параллелограмм»
В: «Диагонали четырехугольника MNPQ в точке пересечения делятся пополам».
Импликация A  В: «Если четырехугольник MNPQ параллелограмм, то его диагонали в точке пересечения делятся пополам».
В: «Если четырехугольник MNPQ параллелограмм, то его диагонали в точке пересечения делятся пополам».
Если А =1 и В =1, то (A  В)= 1 – получили известную теорему из курса геометрии основной школы.
В)= 1 – получили известную теорему из курса геометрии основной школы.
С помощью таблиц истинности можно доказать логические формулы:
1. 
2. 
(д) Логической операции «эквиваленция» соответствует логическая связка «равносильно», «равнозначно», ее символ  , A
, A  B – обозначение эквиваленции высказываний А и В.
B – обозначение эквиваленции высказываний А и В.
Опр. 6. Эквиваленцией двух высказываний А и В называется новое высказывание С=(A  B), полученное соединением этих высказываний посредством связки «равносильно» (
B), полученное соединением этих высказываний посредством связки «равносильно» ( ), истинность которого определяется таблицей (Табл 5)
), истинность которого определяется таблицей (Табл 5)
| A
| B
| A  B B
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Табл 5
Таблица показывает, что эквиваленция истинна тогда, когда оба высказывания имеют одинаковые значения истинности. Выражение A  B читается:
B читается:
- А равносильно В;
- А равнозначно В;
- А тогда и только тогда, когда В.
Пример 1.
1). Выберем объекты исследования:
|
| Множество натуральных чисел: N={1,2,3,…n…}
|
| Множество множеств:
М={  } }
|
2). Введем операции с элементами в каждом множестве:
|
| Сложение натуральных чисел:
a+b
|
| Объединение множеств:
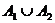
|
3). Введенные операции во множествах M и N обладают свойствами:
|
| 1) a+b=b+a –переместительное
2) (a+b)+c=a+(b+c) - сочетательное
|
| 1) 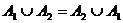 - переместительное
2) - переместительное
2)  - сочетательное - сочетательное
|
4). Введем отношения в множествах N и M:
|
| Равенство натуральных чисел:
а=b
|
| Равносильность множеств:

|
5). Введенные отношения во множествах M и N обладают свойствами:
|
| 1) a=а – рефлексивности отношения равенства;
2) (а=b)  (b=a) – симметричности отношения равенства;
3) (b=a) – симметричности отношения равенства;
3)  - транзитивности отношения равенства. - транзитивности отношения равенства.
|
| 1)  - рефлексивности отношения равносильности;
2) - рефлексивности отношения равносильности;
2)  - симметричности отношения равносильности;
3) - симметричности отношения равносильности;
3)  - транзитивности отношения равносильности. - транзитивности отношения равносильности.
|
Рассмотренный пример показывает, насколько сходны свойства некоторых операций и некоторых отношений во множествах различной природы. Такого рода свойства отношений, структуру связей математических объектов ученые абстрагируют и изучают.
ТЕМА V – ОСНОВНЫЕ ПОНЯТИЯ ПОЗИЦИОННОЙ СИСТЕМЫ СЧИСЛЕНИЯ
Признак делимости.
1. Выберем два числа:  , разложим число «а» по основаниям системы счисления – числа 10:
, разложим число «а» по основаниям системы счисления – числа 10:  (1) и будем искать условие, при котором
(1) и будем искать условие, при котором  .
.
1) Разделим на число «b» каждую из разрядных единиц числа «а»:  :
:
 -
-  - неполные частные;
- неполные частные;
 -
-  - остатки от деления степеней 10 на число «b».
- остатки от деления степеней 10 на число «b».
………………..


2) Подставим результаты деления в соотношение (1): 
3) Обозначим S=  - это сумма произведений чисел, обозначаемых цифрами
- это сумма произведений чисел, обозначаемых цифрами  числа «а», на остатки от деления соответствующих степеней 10 на число «b».
числа «а», на остатки от деления соответствующих степеней 10 на число «b».
4)  , число
, число  делится на число «b», поэтому «а» разделится на число «b», если на «b» разделится число «S».
делится на число «b», поэтому «а» разделится на число «b», если на «b» разделится число «S».
ТЕМА VII - ОСНОВНЫЕ ПОНЯТИЯ ФУНКЦИИ
1. Понятие функции одной переменной.
2. Свойства функции y=f(x.
3. Прямая пропорциональная зависимость величин.
ТЕМА VIII – ОСНОВНЫЕ ПОНЯТИЯ УРАВНЕНИЙ
Числовые выражения.
Числовые выражения
Опр.1. Математическим выражением называется последовательность букв латинского алфавита, чисел, знаков действий и скобок. Например,  .
.
Если выражение состоит только из чисел, то выражение называется числовым, если выражение содержит буквы, то оно называется выражением с переменными. Например,  -выражение числовое,
-выражение числовое, 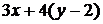 -выражение с двумя переменными. Значением числового выражения называется число, полученное в результате последовательного выполнения операций, указанных в выражении. Например, значение выражения
-выражение с двумя переменными. Значением числового выражения называется число, полученное в результате последовательного выполнения операций, указанных в выражении. Например, значение выражения  равно
равно  , а значения выражения
, а значения выражения  не существует, так как на нуль делить нельзя.
не существует, так как на нуль делить нельзя.
Значениями переменной называются числа, которые можно подставить в выражение вместо переменной. Множество таких чисел называется областью определения выражения. Например, в выражение  вместо
вместо  можно подставлять любые числа
можно подставлять любые числа  ; в выражение
; в выражение  любые числа
любые числа  , кроме
, кроме  , так как при этом в знаменателе получаем число нуль.
, так как при этом в знаменателе получаем число нуль.
Пусть  -два числовых выражения. Соединим их знаками равенства (=) или неравенства (>,<). Тогда:
-два числовых выражения. Соединим их знаками равенства (=) или неравенства (>,<). Тогда:  числовое равенство;
числовое равенство;  -числовые неравенства. Например,
-числовые неравенства. Например,  -числовое равенство,
-числовое равенство,  -числовое неравенство.
-числовое неравенство.
Опр.2. Числовым равенством называется истинное высказывание  .
.
Числовые равенства обладают свойствами: а) рефлексивности:  ,б) симметричности:
,б) симметричности:  , в) транзитивности:
, в) транзитивности:  .
.
Опр.3. Числовым неравенством называется истинное высказывание вида  .
.
Число  больше числа
больше числа  , если
, если  , обозначается:
, обозначается:  , число
, число  меньше числа
меньше числа  , если
, если  , обозначается:
, обозначается:  .
.
Опр.4. Два неравенства называются неравенствами одинакового смысла, если они содержат один и тот же знак неравенства. Два неравенства называются неравенствами противоположного смысла, если они содержат разные знаки неравенства. Например,  и
и  - неравенства одинакового смысла,
- неравенства одинакового смысла,  ,
,  - неравенства противоположного смысла.
- неравенства противоположного смысла.
Числовые неравенства обладают свойствами:
а) антисимметричности:  , например
, например  ;
;
б) транзитивности:  , например,
, например,  ;
;
в) монотонности:  , например,
, например,  ;
;
г)  -неравенства одинакового смысла можно почленно складывать, например,
-неравенства одинакового смысла можно почленно складывать, например,  ;
;
д) при 
 -при умножении обеих частей неравенства на положительное число знак неравенства сохраняется; например,
-при умножении обеих частей неравенства на положительное число знак неравенства сохраняется; например,
 или
или  ;
;
е) при 
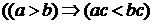 - при умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный, например,
- при умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный, например,  или
или  ;
;
ж) при 
 - неравенства одинакового смысла при всех положительных его частях можно почленно перемножать, сохраняя знак неравенства, например,
- неравенства одинакового смысла при всех положительных его частях можно почленно перемножать, сохраняя знак неравенства, например,  ;
;
з) 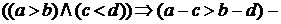 неравенства противоположного смысла можно почленно вычитать, сохраняя знак неравенства уменьшаемого, например,
неравенства противоположного смысла можно почленно вычитать, сохраняя знак неравенства уменьшаемого, например,  или
или  .
.
ТЕМА X – ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ ЕВКЛИДА
1. Система аксиом Д.Гильберта на плоскости (геометрия Евклида)
Рис.8
Опр. 6. Углом называется фигура, состоящая из двух лучей [ OA);[ OB), с общим началом О и одного из тех двух множеств точек, на которые эти лучи разбивают точки плоскости.
Лучи ([ OA);[ OB)) – это стороны угла, точка О – вершина угла.
1)([ OA);[ OB)),  -это один угол,
-это один угол,
2)([ OA);[ OB)),  -это второй угол.
-это второй угол.
В начальной школе под углом чаще понимают угол именно в таком смысле.
Если оба луча лежат на одной прямой, то возможны случаи:
1) лучи [ ОА), [ ОВ) – не совпадают;
2) лучи [ ОА), [ ОВ) – совпадают.
Случай 1): если лучи не совпадают, то плоскость этими лучами разбивается на два множества  и
и  , ситуация соответствует принятому определению, имеем два угла: [ ОА), [ ОВ) и область
, ситуация соответствует принятому определению, имеем два угла: [ ОА), [ ОВ) и область  ;
;
[ ОА), [ ОВ) и область  .
.
Такие углы называются развернутыми (Рис.9).
Опр. 7. Угол называется развернутым, если лучи ([ OA);[ OB)) лежат на одной прямой и не совпадают.

Рис.9
Случай 2): если лучи совпадают, то плоскость между двумя лучами на два множества не разбивается. Образуется только одно множество G, две точки которого можно соединить ломаной линией MNPRS (Рис.10). Для единообразия можно считать, что имеем 2 множества:  - не пустое, и
- не пустое, и 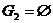 .
.

Рис.10
Опр.8. Угол называется нулевым, если его стороны совпадают.
Опр.9. Два угла называются смежными, если их объединение есть угол развернутый, а пересечение - их общая сторона.
Иначе, угол является развернутым, если: 1)  , 2)
, 2)  - луч [ОВ) (Рис. 11)
- луч [ОВ) (Рис. 11)

Рис. 11
.
Опр. 10. Угол называется прямым, если он равен своему смежному углу.
Наиболее часто встречающимися геометрическими фигурами на плоскости являются многоугольники и их простейшие виды. Если у многоугольника «n» сторон, то говорят об n- угольнике, если n =3. то это треугольник, если n =4, то четырехугольник и т.д. Опираясь на метод определения математического понятия через род и видовое отличие, проведем классификацию простейших геометрических фигур, с которыми могут встретиться учащиеся начальной школы при изучении математики.
Опр. 11. Треугольником называется многоугольник с тремя углами (в обычном курсе принято говорить о треугольнике как о фигуре с тремя сторонами).
Классификация треугольников, их виды, свойства сторон и углов, признаки равенства и подобия хорошо известны из курса математики основной школы.
Опр.12. Четырехугольником называется многоугольник, имеющий 4 угла.
К четырехугольникам относятся квадраты, прямоугольники, ромбы, параллелограммы, трапеции, их свойства изучаются в курсе математики основной школы.
Опр. 13. Трапецией называется четырехугольник, имеющий одну пару параллельных сторон.
Опр. 14 (1). Параллелограммом называется трапеция с параллельными боковыми сторонами.
Опр.14(2). Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.
Опр.15. Ромбом называется параллелограмм с равными смежными сторонами.
Опр. 16. Прямоугольником называется параллелограмм с прямым углом.
Опр. 17. Квадратом называется ромб с прямым углом.
Опр. 18. Квадратом называется прямоугольник с равными смежными сторонами
Все приведенные определения геометрических понятий сформулированы на основе выделения родового понятия и его и видового признака.
ТЕМА XII – ОСНОВНЫЕ ПОНЯТИЯ ВЕЛИЧИНЫ
Общее понятие величины.
Длина отрезка как величина.
Общее понятие величины
Геометрические фигуры обладают некоторыми свойствами, эти свойства обладают особенностями.
Во – первых, отмечается наличие или отсутствие конкретного свойства у данной геометрической фигуры: ограниченность (отрезка), равенство всех сторон у квадрата.
Во – вторых, про некоторые свойства геометрических фигур можно утверждать, что они обладают этими свойствами в большем или меньшем количестве. Даже можно утверждать, какое количество единиц данного свойства содержит эта фигура. К таким свойствам относятся:
- свойство отрезка иметь длину;
- свойство плоской фигуры иметь площадь;
- свойство тела иметь объем.
При рассмотрении такого свойства фигур ставятся задачи:
1) Когда следует считать, обладает или нет фигура интересующим нас свойством?
2) Каким способом можно определить количество этого свойства у данной фигуры?
Другими словами: каким способом можно сопоставить данной фигуре некоторое неотрицательное число, показывающее сколько единиц данного свойства имеется у фигуры. Если фигура обладает одним из указанных свойств, то количество этого свойства называют:
- мера длины;
- мера площади,
- мера объема, или просто: длина, площадь, объем.
Длина, площадь, объем – это числовые характеристики геометрических фигур. Нахождение численного значения данной величины фигуры называется измерением.
Опр. 1. Геометрическая фигура обладает свойством величины, если ей можно по определенному закону поставить в соответствие некоторую числовую характеристику, обладающую свойствами инвариантности и аддитивности.
Замечание 1. Смысл терминов «инвариантность» и «аддитивность» рассмотрим позже.
Сформулируем определение понятия величины, опираясь на аксиоматический метод разработки теории.
1) Зададим некоторое множество элементов – S.
2) В построенном множестве S введем отношения между элементами:
 - отношение эквивалентности;
- отношение эквивалентности;
 - состоять из (т.е. элемент «а» состоит из элементов «b» и «с»).
- состоять из (т.е. элемент «а» состоит из элементов «b» и «с»).
Опр.2. На множестве S определена величина, если  можно поставить в соответствие неотрицательное действительное число f(a) так, чтобы выполнялись условия:
можно поставить в соответствие неотрицательное действительное число f(a) так, чтобы выполнялись условия:
(1) 
(2)  - свойство аддитивности (add – сложить, прибавить);
- свойство аддитивности (add – сложить, прибавить);
(3) некоторому элементу «е» из множества S соответствует число единица;
(4) пусть в множестве S установлено два вида соответствий (два вида измерений), удовлетворяющих условиям (1), (2), (3).
I – элементу  соответствует число
соответствует число 
II – элементу  соответствует число
соответствует число  ,
,
тогда существует число к> 0 такое, что  - свойство инвариантности (неизменности).
- свойство инвариантности (неизменности).
Длина отрезка как величина
Пусть задано некоторое множество отрезков S ={ a,b,c,…m }, Введем в этом множестве отношение  , означающее равенство отрезков a=b, выражение
, означающее равенство отрезков a=b, выражение  означает, что отрезок «а» состоит из отрезков «b» и «с». обозначим через
означает, что отрезок «а» состоит из отрезков «b» и «с». обозначим через  некоторое положительное действительное число, назовем его мерой отрезка «а».
некоторое положительное действительное число, назовем его мерой отрезка «а».
Опр. 3. Число  называется длиной отрезка
называется длиной отрезка  , если для
, если для  можно поставить в соответствие некоторое число
можно поставить в соответствие некоторое число  так, чтобы выполнялись условия:
так, чтобы выполнялись условия:
(1) 
 =
=  );
);
(2) 
 ; (свойство аддитивности);
; (свойство аддитивности);
(3) 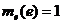 - существует единичный отрезок «е», которому сопоставляется число единица;
- существует единичный отрезок «е», которому сопоставляется число единица;
(4) если для отрезков множества S существуют два единичных отрезка «е» и «f», то можно найти такое число  , что
, что  (свойство инвариантности).
(свойство инвариантности).
Например, е =1см, f =1м, и пусть  см,
см,  м, тогда
м, тогда  , т.е. к=0,01.
, т.е. к=0,01.
Из предыдущего имеем следствия:
1) 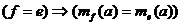 - при замене единичного отрезка «е» на равный ему единичный отрезок «f» длина отрезка не изменится.
- при замене единичного отрезка «е» на равный ему единичный отрезок «f» длина отрезка не изменится.
2)  - если меры отрезков одинаковы, то отрезки измерены одним и тем же единичным отрезком.
- если меры отрезков одинаковы, то отрезки измерены одним и тем же единичным отрезком.
МАТЕМАТИКА (ТЕОРИЯ)
Профиль – начальное образование)
Пояснительная записка
Данный УМК разработан для студентов – заочников направления «Педагогическое образование» по профилю «Начальное образование». По учебному плану на изучение «Математики» выделено всего 14 аудиторных часов, в течение которых преподавателю необходимо ознакомить студентов с теоретическими основами курса математики начального образования.
Запланированных 4 часов лекционных занятий достаточно только для краткого ознакомления с задачами изучения курса, рекомендации списка учебной литературы.
Анализ многих программ по математике, предлагаемых для изучения учащимся начальной школы, показывает, что учитель, работающий в школе или готовится к этой работе, должен иметь как достаточно серьезную теоретическую подготовку, так и обладать развитым математическим и логическим мышлением. В связи с этим в подготовку бакалавра – будущего учителя начального образования – целесообразно включить не только изучение фактического содержания курса математики начального образования (множеств, натуральных чисел, делимости чисел, систем счисления, простейших понятий функции и уравнения), но и некоторые сведения методологического характера - элементов математической логики, методов определения математического понятия, аксиоматического метода построения теории и др.
В дополнение к существующей учебной литературе для подготовки учителя начального образования по математике автор разработанного УМК предлагает необходимый, на его взгляд, теоретический материал по дисциплине «Математика».
Предложенный курс разбит на темы, в процессе изложения содержания тем выделены отдельные пункты, не предполагается никаких почасовых ограничений, материал предназначен в основном, для самостоятельного изучения курса математики.
ТЕМА I - МНОЖЕСТВА
Понятие множества, геометрическая интерпретация числовых множеств на числовой прямой





 . При этом, если А=1, то
. При этом, если А=1, то  , A
, A  , A
, A  , причем, по таблице - A
, причем, по таблице - A  является дизъюнкцией строгого неравенства
является дизъюнкцией строгого неравенства  и равенства
и равенства  .
. , A
, A  А». Смысл этого символа рассмотрим позже.
А». Смысл этого символа рассмотрим позже.

 , A
, A  }
}
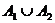
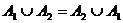 - переместительное
2)
- переместительное
2)  - сочетательное
- сочетательное

 - транзитивности отношения равенства.
- транзитивности отношения равенства.
 - рефлексивности отношения равносильности;
2)
- рефлексивности отношения равносильности;
2)  - симметричности отношения равносильности;
3)
- симметричности отношения равносильности;
3)  - транзитивности отношения равносильности.
- транзитивности отношения равносильности.
 , разложим число «а» по основаниям системы счисления – числа 10:
, разложим число «а» по основаниям системы счисления – числа 10:  (1) и будем искать условие, при котором
(1) и будем искать условие, при котором  .
. :
: -
-  - неполные частные;
- неполные частные; -
-  - остатки от деления степеней 10 на число «b».
- остатки от деления степеней 10 на число «b».


 - это сумма произведений чисел, обозначаемых цифрами
- это сумма произведений чисел, обозначаемых цифрами  числа «а», на остатки от деления соответствующих степеней 10 на число «b».
числа «а», на остатки от деления соответствующих степеней 10 на число «b». , число
, число  делится на число «b», поэтому «а» разделится на число «b», если на «b» разделится число «S».
делится на число «b», поэтому «а» разделится на число «b», если на «b» разделится число «S». .
. -выражение числовое,
-выражение числовое, 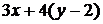 -выражение с двумя переменными. Значением числового выражения называется число, полученное в результате последовательного выполнения операций, указанных в выражении. Например, значение выражения
-выражение с двумя переменными. Значением числового выражения называется число, полученное в результате последовательного выполнения операций, указанных в выражении. Например, значение выражения  равно
равно  , а значения выражения
, а значения выражения  не существует, так как на нуль делить нельзя.
не существует, так как на нуль делить нельзя. вместо
вместо  можно подставлять любые числа
можно подставлять любые числа  ; в выражение
; в выражение  любые числа
любые числа  , так как при этом в знаменателе получаем число нуль.
, так как при этом в знаменателе получаем число нуль. -два числовых выражения. Соединим их знаками равенства (=) или неравенства (>,<). Тогда:
-два числовых выражения. Соединим их знаками равенства (=) или неравенства (>,<). Тогда:  числовое равенство;
числовое равенство;  -числовые неравенства. Например,
-числовые неравенства. Например,  -числовое равенство,
-числовое равенство,  -числовое неравенство.
-числовое неравенство. .
. ,б) симметричности:
,б) симметричности:  , в) транзитивности:
, в) транзитивности:  .
. .
. больше числа
больше числа  , если
, если  , обозначается:
, обозначается:  , число
, число  , обозначается:
, обозначается:  .
. и
и  - неравенства одинакового смысла,
- неравенства одинакового смысла,  ,
,  - неравенства противоположного смысла.
- неравенства противоположного смысла. , например
, например  ;
; , например,
, например,  ;
; , например,
, например,  ;
; -неравенства одинакового смысла можно почленно складывать, например,
-неравенства одинакового смысла можно почленно складывать, например,  ;
;
 -при умножении обеих частей неравенства на положительное число знак неравенства сохраняется; например,
-при умножении обеих частей неравенства на положительное число знак неравенства сохраняется; например, или
или  ;
;
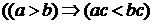 - при умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный, например,
- при умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный, например,  или
или  ;
;
 - неравенства одинакового смысла при всех положительных его частях можно почленно перемножать, сохраняя знак неравенства, например,
- неравенства одинакового смысла при всех положительных его частях можно почленно перемножать, сохраняя знак неравенства, например,  ;
;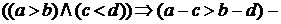 неравенства противоположного смысла можно почленно вычитать, сохраняя знак неравенства уменьшаемого, например,
неравенства противоположного смысла можно почленно вычитать, сохраняя знак неравенства уменьшаемого, например,  или
или  .
. -это один угол,
-это один угол, -это второй угол.
-это второй угол.
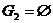 .
.
 , 2)
, 2)  - луч [ОВ) (Рис. 11)
- луч [ОВ) (Рис. 11)
 - отношение эквивалентности;
- отношение эквивалентности; - состоять из (т.е. элемент «а» состоит из элементов «b» и «с»).
- состоять из (т.е. элемент «а» состоит из элементов «b» и «с»). можно поставить в соответствие неотрицательное действительное число f(a) так, чтобы выполнялись условия:
можно поставить в соответствие неотрицательное действительное число f(a) так, чтобы выполнялись условия:
 - свойство аддитивности (add – сложить, прибавить);
- свойство аддитивности (add – сложить, прибавить); соответствует число
соответствует число 
 ,
, - свойство инвариантности (неизменности).
- свойство инвариантности (неизменности). , означающее равенство отрезков a=b, выражение
, означающее равенство отрезков a=b, выражение  означает, что отрезок «а» состоит из отрезков «b» и «с». обозначим через
означает, что отрезок «а» состоит из отрезков «b» и «с». обозначим через  некоторое положительное действительное число, назовем его мерой отрезка «а».
некоторое положительное действительное число, назовем его мерой отрезка «а». так, чтобы выполнялись условия:
так, чтобы выполнялись условия:
 );
);
 ; (свойство аддитивности);
; (свойство аддитивности);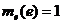 - существует единичный отрезок «е», которому сопоставляется число единица;
- существует единичный отрезок «е», которому сопоставляется число единица; , что
, что  (свойство инвариантности).
(свойство инвариантности). см,
см,  м, тогда
м, тогда  , т.е. к=0,01.
, т.е. к=0,01.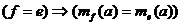 - при замене единичного отрезка «е» на равный ему единичный отрезок «f» длина отрезка не изменится.
- при замене единичного отрезка «е» на равный ему единичный отрезок «f» длина отрезка не изменится. - если меры отрезков одинаковы, то отрезки измерены одним и тем же единичным отрезком.
- если меры отрезков одинаковы, то отрезки измерены одним и тем же единичным отрезком.

