Метод восстановления трехмерной информации по трем ортогональным проекциям (чертежи: вид сверху, сбоку и спереди). Проекция произвольного вида на плоскость  получается с помощью следующего преобразования общего вида
получается с помощью следующего преобразования общего вида
 (*)
(*)
Аналогично можно записать проекции на плоскость  и
и  . Мы будем рассматривать вопросы восстановления в случае плоскости
. Мы будем рассматривать вопросы восстановления в случае плоскости  . Раскроем уравнение (*):
. Раскроем уравнение (*):
 ;
;  ;(**)
;(**)
 .
.
Подставим (**)  в
в  и
и  :
:
 ;(***)
;(***)
 .
.
На систему уравнений (***) можно смотреть с трех точек зрения.
1) пусть известны  ,
, 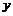 ,
, 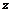 и матрица
и матрица  . Найти
. Найти  ,
,  . Это – задача построения проекции. Решение получается непосредственно из уравнения (***).
. Это – задача построения проекции. Решение получается непосредственно из уравнения (***).
 пусть известны матрица
пусть известны матрица  и координаты
и координаты 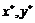 . Требуется найти координаты
. Требуется найти координаты  . Это – задача восстановления трехмерной информации по проекции известного вида. При этом система уравнений (***) не имеет решения (два уравнения с тремя неизвестными). Для получения искомых координат требуется иметь две различные проекции, матрицы которых
. Это – задача восстановления трехмерной информации по проекции известного вида. При этом система уравнений (***) не имеет решения (два уравнения с тремя неизвестными). Для получения искомых координат требуется иметь две различные проекции, матрицы которых  и
и  известны, и, кроме того, известны координаты одной и той же точки пространства на каждой из этих проекций
известны, и, кроме того, известны координаты одной и той же точки пространства на каждой из этих проекций  и
и  .(Пример – две фотографии объекта). Тогда имеем две пары уравнений вида (***), которое в матричном виде можно записать как
.(Пример – две фотографии объекта). Тогда имеем две пары уравнений вида (***), которое в матричном виде можно записать как
 , где
, где




Получим систему из 4-х уравнений с тремя неизвестными. Решение этой системы может быть получено только приближенно, методом подбора. Тем не менее, то, что мы получили – это метод восстановления трехмерной информации по двум различным, но известным проекциям.
 Пусть известны координаты точки в трехмерном пространстве
Пусть известны координаты точки в трехмерном пространстве  и ее координаты на проекции
и ее координаты на проекции  . Необходимо определить матрицу
. Необходимо определить матрицу  , то есть вид проекции. Теперь два уравнения (***) содержат 12 неизвестных. Для получения решения нам нужно иметь 6 таких пар уравнений, т.е. знать координаты в пространстве и на проекции 6 так называемых опорных точек. Имея такую априорную информацию, мы можем восстановить вид проекции, то есть найти элементы матрицы
, то есть вид проекции. Теперь два уравнения (***) содержат 12 неизвестных. Для получения решения нам нужно иметь 6 таких пар уравнений, т.е. знать координаты в пространстве и на проекции 6 так называемых опорных точек. Имея такую априорную информацию, мы можем восстановить вид проекции, то есть найти элементы матрицы  , и затем использовать этот результат для восстановления трехмерных координат других, не опорных точек, по методу, рассмотренному в предыдущем случае. В матричной форме система 12 уравнений может быть записана следующим образом:
, и затем использовать этот результат для восстановления трехмерных координат других, не опорных точек, по методу, рассмотренному в предыдущем случае. В матричной форме система 12 уравнений может быть записана следующим образом:
 , где
, где 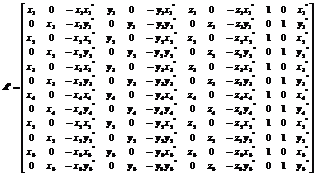

6. Математическое описание плоских кривых. Представление канонических сечений, окружности, эллипса, параболы, гиперболы.
С одной стороны, любая кривая может быть представлена совокупностью точек, над которыми затем могут выполняться рассмотренные ранее преобразования. При этом важно, чтобы точки кривой располагались достаточно близко друг к другу, иначе они будут давать неверное представление о форме кривой. Математическое описание кривой имеет целый ряд преимуществ перед описанием через совокупность точек. Основные преимущества следующие:
1) Математическое описание является точным; оно позволяет вычислить такие характеристики кривой, как наклон, радиус кривизны и т. д.
2) Оно компактно может быть занесено в память.
3) Математическое описание позволяет легко менять форму кривых; результаты преобразования кривых известной матрице 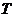 может быть также представлены в форме математического описания.
может быть также представлены в форме математического описания.
Теперь рассмотрим различные методы математического описания плоских кривых. Математически кривая может быть представлена в параметрической и непараметрической форме. Непараметрическое описание задается в виде явной функции  либо в виде неявной функции
либо в виде неявной функции  Задание в виде явной функции имеет один существенный недостаток: этим способом нельзя определить многозначные кривые, то есть такие, в которых одному значению
Задание в виде явной функции имеет один существенный недостаток: этим способом нельзя определить многозначные кривые, то есть такие, в которых одному значению  может соответствовать два и более значения
может соответствовать два и более значения 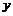 . Неявные функции лишены этого недостатка.
. Неявные функции лишены этого недостатка.
При параметрическом задании кривой каждая координата точки на кривой представляется как функция одного параметра.
Плоские параметрические кривые с одним параметром представляются в виде  где
где  - параметр.
- параметр.
Геометрическая интерпретация математических описаний следующая. Для непараметрических функций - это геометрическое место точек плоскости, удовлетворяющих уравнениям 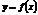 или
или  . То есть все точки
. То есть все точки  , удовлетворяющие этим уравнениям, принадлежат кривой, и ни одна точка, координаты которой не удовлетворяют уравнениям, не принадлежит кривой. Параметрические кривые интерпретируются как траектория движения некоего точечного объекта. При этом
, удовлетворяющие этим уравнениям, принадлежат кривой, и ни одна точка, координаты которой не удовлетворяют уравнениям, не принадлежит кривой. Параметрические кривые интерпретируются как траектория движения некоего точечного объекта. При этом  имеет смысл времени. Положение конкретной точки определяется парой
имеет смысл времени. Положение конкретной точки определяется парой 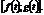
Конические сечения - это сечения правильного конуса некоторой плоскостью. В зависимости от взаимного расположения секущей плоскости и оси симметрии конуса сечение будет являться кривой, относящейся к следующим четырем типам: окружность, эллипс, парабола и гипербола. Все эти кривые относятся к кривым второй степени, то есть могут быть описаны уравнениями второй степени,
 где хоть один из
где хоть один из 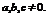 Вопрос о том, какую именно кривую представляет это уравнение, определяется значениями его коэффициентов. Можно показать, что если величина дискриминанта
Вопрос о том, какую именно кривую представляет это уравнение, определяется значениями его коэффициентов. Можно показать, что если величина дискриминанта  то это парабола;
то это парабола;
если  - эллипс или окружность;
- эллипс или окружность;
если  – гипербола.
– гипербола.
ОКРУЖНОСТЬ.
Окружность с центром в точке  и радиусом r задается уравнением
и радиусом r задается уравнением 
Раскрывая скобки: 
Или  где
где 


Таким образом, уравнение окружности содержит три неизвестных коэффициента. Соответственно, для построения окружности (или дуги окружности) необходимо знать три точки, через которые она проходит: две концевые точки дуги и одну промежуточную. Однако построение дуги окружности через три заданные точки - это не единственный способ. Дуга окружности будет определена, если известны
1) две концевые точки и центр;
2) одна концевая точка и наклон в начале и в конце и т. д.
ЭЛЛИПС.
Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная 
Уравнение эллипса в канонической форме:
 ;
; 
Приведем его к общему виду:


то есть


то есть уравнение определяет эллипс, если 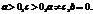
ПАРАБОЛА.
Парабола есть геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Уравнение параболы
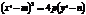
 т.е.
т.е. 
При 
( – координаты вершины;
– координаты вершины; 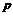 – параметр, определяющий расстояние между директрисой и фокусом)
– параметр, определяющий расстояние между директрисой и фокусом)
Приведенное уравнение представляет параболу, осью симметрии которой является  . Если
. Если  и
и  поменять местами, осью симметрии будет
поменять местами, осью симметрии будет 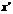 . Если
. Если  , то ветви параболы будут направлены в положительную сторону (вверх или вправо), если
, то ветви параболы будут направлены в положительную сторону (вверх или вправо), если  - в отрицательную сторону (вниз или влево).
- в отрицательную сторону (вниз или влево).
ГИПЕРБОЛА.
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.Уравнение:
 или
или 
Здесь  и
и  ;
; 

Будем рассматривать гиперболу, центрированную относительно начала координат и с положительной полуосью x в качестве оси симметрии.
Тогда в непараметрическом виде ее уравнение запишется как 
7. Представление пространственных кривых.
параметрически.
Непараметрическое явное задание: 
Непараметрическое неявное задание - кривая на пересечении двух поверхностей: 
Параметрическое задание: 

Простейший пример - цилиндрическая спираль:

 - радиус,
- радиус,  - шаг спирали.
- шаг спирали.
Очень часто аналитическое описание неизвестно. В этом случае ставится задача проведения кривой через ряд заданных точек, или проведения кривой, имеющей более сложную зависимость от заданных точек.



 получается с помощью следующего преобразования общего вида
получается с помощью следующего преобразования общего вида (*)
(*) и
и  . Мы будем рассматривать вопросы восстановления в случае плоскости
. Мы будем рассматривать вопросы восстановления в случае плоскости  ;
;  ;(**)
;(**) .
. в
в  и
и  :
: ;(***)
;(***) .
. ,
, 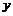 ,
, 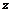 и матрица
и матрица  . Найти
. Найти  ,
,  . Это – задача построения проекции. Решение получается непосредственно из уравнения (***).
. Это – задача построения проекции. Решение получается непосредственно из уравнения (***). пусть известны матрица
пусть известны матрица 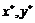 . Требуется найти координаты
. Требуется найти координаты  . Это – задача восстановления трехмерной информации по проекции известного вида. При этом система уравнений (***) не имеет решения (два уравнения с тремя неизвестными). Для получения искомых координат требуется иметь две различные проекции, матрицы которых
. Это – задача восстановления трехмерной информации по проекции известного вида. При этом система уравнений (***) не имеет решения (два уравнения с тремя неизвестными). Для получения искомых координат требуется иметь две различные проекции, матрицы которых  известны, и, кроме того, известны координаты одной и той же точки пространства на каждой из этих проекций
известны, и, кроме того, известны координаты одной и той же точки пространства на каждой из этих проекций  и
и  .(Пример – две фотографии объекта). Тогда имеем две пары уравнений вида (***), которое в матричном виде можно записать как
.(Пример – две фотографии объекта). Тогда имеем две пары уравнений вида (***), которое в матричном виде можно записать как , где
, где



 Пусть известны координаты точки в трехмерном пространстве
Пусть известны координаты точки в трехмерном пространстве  и ее координаты на проекции
и ее координаты на проекции  . Необходимо определить матрицу
. Необходимо определить матрицу  , где
, где 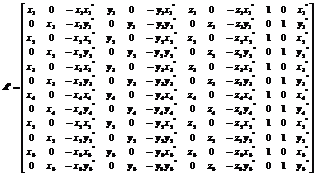

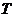 может быть также представлены в форме математического описания.
может быть также представлены в форме математического описания. либо в виде неявной функции
либо в виде неявной функции  Задание в виде явной функции имеет один существенный недостаток: этим способом нельзя определить многозначные кривые, то есть такие, в которых одному значению
Задание в виде явной функции имеет один существенный недостаток: этим способом нельзя определить многозначные кривые, то есть такие, в которых одному значению  где
где  - параметр.
- параметр.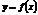 или
или  . То есть все точки
. То есть все точки  , удовлетворяющие этим уравнениям, принадлежат кривой, и ни одна точка, координаты которой не удовлетворяют уравнениям, не принадлежит кривой. Параметрические кривые интерпретируются как траектория движения некоего точечного объекта. При этом
, удовлетворяющие этим уравнениям, принадлежат кривой, и ни одна точка, координаты которой не удовлетворяют уравнениям, не принадлежит кривой. Параметрические кривые интерпретируются как траектория движения некоего точечного объекта. При этом 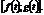
 где хоть один из
где хоть один из 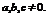 Вопрос о том, какую именно кривую представляет это уравнение, определяется значениями его коэффициентов. Можно показать, что если величина дискриминанта
Вопрос о том, какую именно кривую представляет это уравнение, определяется значениями его коэффициентов. Можно показать, что если величина дискриминанта  то это парабола;
то это парабола; - эллипс или окружность;
- эллипс или окружность; – гипербола.
– гипербола. и радиусом r задается уравнением
и радиусом r задается уравнением 

 где
где 



 ;
; 




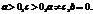

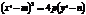
 т.е.
т.е. 

 – координаты вершины;
– координаты вершины; 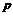 – параметр, определяющий расстояние между директрисой и фокусом)
– параметр, определяющий расстояние между директрисой и фокусом) . Если
. Если  и
и  поменять местами, осью симметрии будет
поменять местами, осью симметрии будет 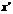 . Если
. Если  , то ветви параболы будут направлены в положительную сторону (вверх или вправо), если
, то ветви параболы будут направлены в положительную сторону (вверх или вправо), если  - в отрицательную сторону (вниз или влево).
- в отрицательную сторону (вниз или влево). или
или 
 и
и  ;
; 







 - радиус,
- радиус,  - шаг спирали.
- шаг спирали.


