Геометрический смысл определенного интеграла
Понятие определенного интеграла введено таким образом, что в случае, когда функция y = f(x) неотрицательна на отрезке [a;b] и непрерывна на нем, где a < b,

численно равен площади S под кривой y = f(x) на [a; b] (рис. 3).
Рисунок. 3

Действительно, при стремлении  к нулю ломаная (рис. 4) неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой.
к нулю ломаная (рис. 4) неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой.
Рисунок. 4

Учитывая сказанное, можно указать значения некоторых интегралов, используя известные планиметрические формулы для площадей плоских фигур. Например,
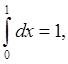

 и т.д.
и т.д.
(Первый из интегралов – площадь квадрата со стороной единичной длины; второй – площадь прямоугольного треугольника, оба катета которого единичной длины; третий – площадь четверти круга единичного радиуса).
Методы интегрирования определенных интегралов заменой переменной и по частым.
Метод замены переменной в определенном интеграле
Пусть функция  непрерывна на отрезке
непрерывна на отрезке 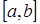 , а функция
, а функция  непрерывна на
непрерывна на  , причем
, причем  ,
,  и для всех
и для всех  выполняется
выполняется  . Тогда
. Тогда
 .
.
Пример 1. Вычислить интеграл  .
.
Решение.
Обозначим  , тогда
, тогда  ,
,  . Подставим старые пределы интегрирования в формулу
. Подставим старые пределы интегрирования в формулу  , получим новые пределы интегрирования
, получим новые пределы интегрирования 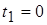 ,
,  . Следовательно,
. Следовательно,
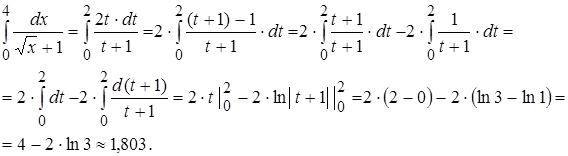
2. Метод интегрирования по частям
Пусть функции  и
и  имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 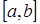 . Тогда
. Тогда
 .
.
Формула интегрирования по частям в определенном интеграле.
Пример.

Несобственные интегралы с бесконечными пределами.
При построении определенного интеграла 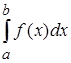 предполагалось, что выполняется два условия:
предполагалось, что выполняется два условия:
пределы интегрирования  и
и 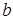 конечны;
конечны;
подынтегральная функция  ограничена на отрезке интегрирования
ограничена на отрезке интегрирования 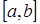 .
.
Интегралы с бесконечными пределами интегрирования или от неограниченных функций называются несобственными интегралами.
Пусть  определена на промежутке
определена на промежутке  и интегрируема на любом отрезке
и интегрируема на любом отрезке 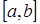 , где
, где  .
.
Несобственным интегралом с бесконечным пределом интегрирования (интегралом 1-го рода) называется предел интеграла 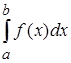 при
при  :
:
 .
.
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, а если предел не существует или равен  , то расходящимся.
, то расходящимся.
Пусть  - первообразная функция для
- первообразная функция для  на промежутке
на промежутке  . Тогда можно применить формулу Ньютона-Лейбница:
. Тогда можно применить формулу Ньютона-Лейбница:
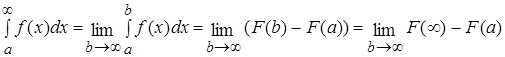 .
.
Обозначая  , формулу можно записать так:
, формулу можно записать так:
 .
.
Пример 7. 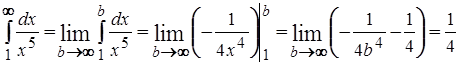 .
.
Данный интеграл является сходящимся.
Геометрически несобственный интеграл от  дает площадь бесконечной криволинейной трапеции, ограниченной сверху линией
дает площадь бесконечной криволинейной трапеции, ограниченной сверху линией  , слева
, слева  , снизу осью ОХ. Если интеграл
, снизу осью ОХ. Если интеграл  сходится – площадь конечна, а если расходится – площадь бесконечна.
сходится – площадь конечна, а если расходится – площадь бесконечна.

0 

Аналогично определяется несобственный интеграл с бесконечным верхним пределом:
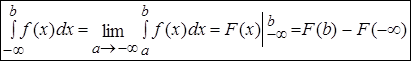
и несобственный интеграл с обоими бесконечными пределами:
 .
.
Пример 8.

Данный интеграл является сходящимся.





 к нулю ломаная (рис. 4) неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой.
к нулю ломаная (рис. 4) неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой.
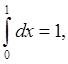

 и т.д.
и т.д. непрерывна на отрезке
непрерывна на отрезке 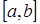 , а функция
, а функция  непрерывна на
непрерывна на  , причем
, причем  ,
,  и для всех
и для всех  выполняется
выполняется  . Тогда
. Тогда .
. .
. , тогда
, тогда  ,
,  . Подставим старые пределы интегрирования в формулу
. Подставим старые пределы интегрирования в формулу 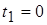 ,
,  . Следовательно,
. Следовательно,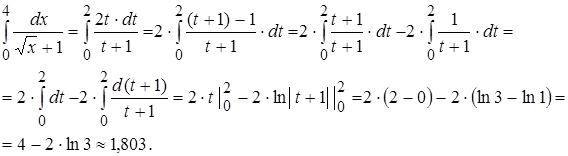
 и
и  имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  .
.
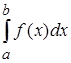 предполагалось, что выполняется два условия:
предполагалось, что выполняется два условия: и
и 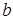 конечны;
конечны; и интегрируема на любом отрезке
и интегрируема на любом отрезке  .
. :
: .
. , то расходящимся.
, то расходящимся. - первообразная функция для
- первообразная функция для 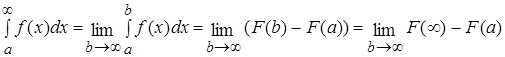 .
. , формулу можно записать так:
, формулу можно записать так: .
.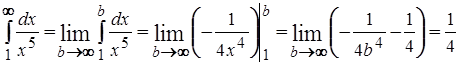 .
. дает площадь бесконечной криволинейной трапеции, ограниченной сверху линией
дает площадь бесконечной криволинейной трапеции, ограниченной сверху линией  , слева
, слева  , снизу осью ОХ. Если интеграл
, снизу осью ОХ. Если интеграл  сходится – площадь конечна, а если расходится – площадь бесконечна.
сходится – площадь конечна, а если расходится – площадь бесконечна.
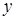

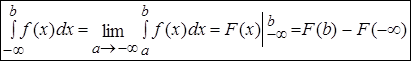
 .
.



