Понятие неопределенного интеграла.
Def Если функция F(x) является первообразной для функции f(x) на промежутке Х, то множество функций {F(x)+C}, где С- произвольная постоянная называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом òf(x)dx=F(x)+C. При этом f(x) называется подынтегральной функцией, f(x)dx- подынтегральным выражением, а переменная х- переменная интегрирования. òf(x)dx- выражает множество всех первообразных для функции f(x) на промежутке Х.
Def Восстановление функции по ее производной или что тоже самое: отыскание неопределенного интеграла называется интегрированием этой функции, т.к. F’(x)=f(x) òF’(x)dx=F(x)+C
Интегрирование- операция обратная дифференцированию и правильность интегрирования определяется следующим образом: мы должны продифференцировать результат и если получили подынтегральную функцию, то операция выполнена верно.
Основные свойства неопределенного интеграла:
1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. (òf(x)dx)’=f(x) и d(òf(x)dx)=f(x)dx Док-во: (òf(x)dx)’=(F(x)+C)’=F’(x)=f(x) и dòf(x)dx=(òf(x)dx)’dx=f(x)dx
2. d(òf(x)dx)=f(x)dx, дифференциал от неопределенного интеграла на промежутке Х равен подынтегральному вырожению.
Док-во: d(òf(x)dx)=d(F(x)+C)=(F(x)+C)’dx=F’(x)dx=f(x)dx
3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е. òdF(x)=F(x)+C. Док-во: т.к. òdF(x)=F’(x)dx, то по определению òF'(x)dx=F(x)+C
4. Постоянный множитель можно вынести из-под знака интеграла, т.е. если k=const¹0, то òkf(x)dx=kòf(x)dx. Док-во: пусть F(x) первообразная для f(x) на промежутке Х, т.е. "xÎX F’(x)=f(x)ÞkF(x) первообразная для kf(x), т.е. (kF(x))’=kF’(x)=kf(x). Из определения следует, что kòf(x)dx=k[F(x)+C]=kF(x)+C1=òkf(x)dx, где С1=кС, ч.т.д.
5. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций отдельно, т.е. ò(f(x)±g(x))dx=òf(x)dx±òg(x)dx. Док-во: пусть F(x) и G(x) являются первообразными для функций f(x) и g(x) на промежутке Х, т.е. "хÎХ F’(x)=f(x), G'(x)=g(x). Тогда функции F(x)±G(x) являются первообразными для функция f(x)±g(x). Следовательно, òf(x)dx±òg(x)dx=(F(x)+C1)±(G(x)+C2)=(F(x)±G(x))+(C1±C2)=[F(x)±G(x)]+C=ò(f(x)±g(x))dx
Это свойство справедливо для любого конечного числа слагаемых.
Методы замены переменной
1. Непосредственное интегрирование.
С помощью табл осн интегралов.
2. Метод подстановки или метод замены переменных.
Достаточно часто введение новой переменой позволяет свести интеграл к табличному
[Т] Пусть функция х=j(t) определена и дифференцируема на некотором промежутке Т и пусть Х- множество значений этой функции, на котором определена функция y=f(x), т.е. на T определена сложная функция y=f[j(t)]. Тогда если на множестве Х функция f(x) имеет первообразную F(x), то справедлива формула òf(x)dx|x=j(t)= òf[j(t)]j’(t)dt. Док-во: Пусть функция F(x) является первообразной для функции f(x) на множестве Х. Рассмотрим на множестве T сложную функцию F[j(t)]. Продифференцируем ее по правилам дифференцирования сложной функции: F’[j(t)]*j’(t)=f’[j(t)]*j’(t)Þ мы получили что эта функция имеет на множестве Т первообразную F[j(t)]. òf[j(t)]*j’(t)dt=F[j(t)]+C=F(x)+C|x=j(t)= òf(x)dx|x=j(t). Получили искомую формулу замены переменных в неопределенном интеграле.
Замечание: При замене переменныхв неопределенном интеграле иногда более удобно задавать не х как функцию t, а задавать t как функцию от х.
Метод неопределенных коэффициентов.
Метод неопределенных коэффициентов
Он заключается в том, чтобы следовать алгоритму: Записать представление 1, привести правую часть к общему знаменателю и группировать при степенях Х, получим дроби с равными знаменателями, присваиваем числители. Получим 2 многочлена, они равны если равны коэффициенты при соответствующих степенях Я, следовательно составляем систему уравнений, приравнивая коэффициенты при соответствующих степенях Х.
Доказательство:
1 вариант (учебники): возьмем любое значение xÎ[a,b] и придадим ему приращение  х¹0 такое, чтобы х+
х¹0 такое, чтобы х+ 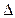 хÎ[a,b], т.е. a£x+
хÎ[a,b], т.е. a£x+ 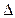 х£b. Тогда функция Ф(х) по определению получит новое значение: Ф(х+
х£b. Тогда функция Ф(х) по определению получит новое значение: Ф(х+ 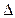 х)=
х)= 
Согласно второму свойству определенного интеграла, имеем: Ф(х+ 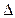 х)=
х)=  +
+  =Ф(х)+
=Ф(х)+  DФ=Ф(х+DХ)-Ф(х),
DФ=Ф(х+DХ)-Ф(х),
т.к. f(x) непрерывна на [a,b] то существует число cÎ[x, x+Dx]:[  =f(c)Dx]. Если устремить приращение аргумента к нулю, получим:
=f(c)Dx]. Если устремить приращение аргумента к нулю, получим:  =f(x) или Ф’(х)=f(x), ч т.д. Можно записать, что òf(x)dx=Ф(x)+C=
=f(x) или Ф’(х)=f(x), ч т.д. Можно записать, что òf(x)dx=Ф(x)+C=  +C
+C
2 вариант (Деревенских) Ф’(х)=  DФ(х)=
DФ(х)=  -
-  =
=  +
+  -
-  =
=  =f(c)* Dx. По теореме о среднем существует cÎ[x, x+Dx]
=f(c)* Dx. По теореме о среднем существует cÎ[x, x+Dx]
 Ф’(x)=
Ф’(x)=  Отсюда следует, что Ф’(x)=f(x)
Отсюда следует, что Ф’(x)=f(x)
Формула Ньютона-Лейбница.
Пусть функция f(x) непрерывна на отрезке [a,b] и имеет на этом отрезке семейство первообразных, одной из которых является Ф(х)=  .
.
[Т] Если функция f(x) непрерывна на [a,b], то верно следующее равенство  . Т.е. определенный интеграл от непрерывной функции равн разности значений любой ее первообразной на верхнем и нижнем пределах интегрирования соответственно. Она называется формулой Ньютона-Лейбница.
. Т.е. определенный интеграл от непрерывной функции равн разности значений любой ее первообразной на верхнем и нижнем пределах интегрирования соответственно. Она называется формулой Ньютона-Лейбница.
Доказательство: Пусть F(x) другая первообразная для функции f(x) на том же отрезке, которая отличается от Ф(х) не более чем на константу, т.е. Ф(х)=F(x)+C,  =F(x)+C, где С- некоторое число, a£x£b. Подставляя в это равенство значение х=а и используя свойство 1, имеем:
=F(x)+C, где С- некоторое число, a£x£b. Подставляя в это равенство значение х=а и используя свойство 1, имеем:  =0, получим: 0=
=0, получим: 0=  , F(a)+C, C=-F(a)
, F(a)+C, C=-F(a)
Т.е. для любого хÎ[a,b]  Полагая здесь х=b получим искомую формулу.
Полагая здесь х=b получим искомую формулу.
А R
DEF
Предел интеграла 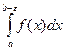 при e®0 называется несобственным интегралом второго рода и обозначается
при e®0 называется несобственным интегралом второго рода и обозначается 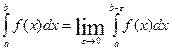 . Если этот предел конечный, то говорят что интеграл существует или сходится, а функцию f(x) называют интегрируемой на промежутке [a,b), если предела нет или он бесконечен, то говорят что интеграл расходится. Аналогично, если особой является точка х=а, то несобственных интеграл второго рода определяется как
. Если этот предел конечный, то говорят что интеграл существует или сходится, а функцию f(x) называют интегрируемой на промежутке [a,b), если предела нет или он бесконечен, то говорят что интеграл расходится. Аналогично, если особой является точка х=а, то несобственных интеграл второго рода определяется как 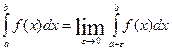 Если функция f(x) не ограничена в окрестности некоторой внутренней точки сÎ[a,b], то по определению полагают
Если функция f(x) не ограничена в окрестности некоторой внутренней точки сÎ[a,b], то по определению полагают 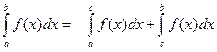 , где несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам предыдущим. Если а и b особые точки, т.е. функция f(x) ограничена и интегрируема на интервале (a,b), то несобственный интеграл второго рода определяется в виде суммы
, где несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам предыдущим. Если а и b особые точки, т.е. функция f(x) ограничена и интегрируема на интервале (a,b), то несобственный интеграл второго рода определяется в виде суммы 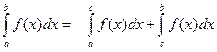 , где с- произвольная точка на (a,b), а несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам.
, где с- произвольная точка на (a,b), а несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам.
19. Метрические, линейные, нормированные, евклидовы пространства.
Функции многих переменных:
Пусть у=f(x), D(f)=XÌR, Е(f)=YÌR
Y=f(x1, x2, … xn) это точки n-мерного Эвклидового пространства
Метрические пространства.
На множестве Х определена фигура метрического пространства, если задана функция r(x,y) двух произвольных элементов этого множества, удовлетворяющих следующим аксиомам:
1. 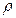 (x,y)=0 тогда и только тогда, когда x=y
(x,y)=0 тогда и только тогда, когда x=y
3. r(x,y)£r(x,z)+r(z,y) (неравенство 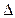 )
)
r(х,y) функция метрики или функция расстояния между точками х и у, принадлежащих Х.
Т.о. метрическое пространство R образует множество Х, с введенной на этом множестве функции расстояния метрического пространства R=(X, r). Если положим, что х=у, то 0£r(x,z)+r(z,y)
Р(x,y) функция метрики или функция расстояния между точками х и у, принадлежащих Х. Т.о. метрическое пространство R образует множество Х, связанной на этом множестве функции расстояния метрического пространства R=(X,р)
Если положим, что х=у, то 0£р(xz)+p(z,x)
2p(x,z)>0 метрика не отрицательна
Введем понятие n-мерного координатного пространства Аn
Def M-мерным координатным пространством Аm называется множетсво всевозможных упорядоченных совокупностей m действительных чисел (x1, x2, x3,…, xm)
Каждую упорядоченную совокупность (x1, x2,…,xm) называют точкой этого пространства и обозначают одной буквой М, при этом числа x1, x2, …,xn называются координатами точки М, что символически записывается так М(x1, x2,…xn)
Чтобы множество Х было метрическим пространством нужно:
Выберем в качестве множества Х n- мерное координатное пространство, возьмем люые х,у принадлежащие этому пространству. Х(х1…хn), y(y1..yn)
Введем функцию расстояния на Х между х и у. Р(х,у)= 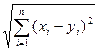
Линейное пространство L
Множество элементов L, содержащее хотя бы один элемент, называется линейным или векторным пространством, если выполнены следующие аксиомы:
1. Любые x,y принадлежат L, однозначно определен 3 элемент z, называемый их суммой, обозначаемый z=x+y, причем справедливые следующие свойства:
А) х+у=у+х (ассоциативность)
Б) (х+у)+z=x+(y+z)
В) Существует элемент (его обычно обозначают за 0) такой, что x+0=X
Г) Существует элемент Х, называемый противоположным, такой что x+x’=0
2) Для любого числа a и любого элемента х принадлежащего L определен элемент у из множества L=  ax при этом справедливы следующие свойства:
ax при этом справедливы следующие свойства:
a(bх)=(ab)х
(b+a)х=aх+bх
a(х+у)=aх+aу
1*x=x
х=х, где ab некоторые числа, х и у точка множества L. Если в аксиоме b и a принадлежат множеству вещественных чисел, то множества L называется действительным линейным пространством
Нормированное пространство N
Возьмем функция f(x)=||x||, ставящая каждому элементу х из множества L в соответствие вещественное число x принадлежащее L – называется нормой в линейном пространстве L, если выполнены следующие аксиомы:
1.f(x)=||x||=0 тогда и только тогда, когда х=0
2. f(aх)=|a|*||x||=|a|*f(x)
3. f(x+y)=||x+y||£||x|| +||y||=f(x)+f(y)
Пространство L, сведенное на этом множестве функцией норма X называют нормированным пространством и обозначают через N. ||x||>0
Следует отметить, что в любом норм. Пространстве может быть введена функция расстояния b(x,y)=||x*y|| как норма элемента х и у.
Def Координатное пространство Аn называют n- мерным евклидовым пространством, если между двумя любыми точками х(х1, х2, …, хn) и у(у1, у2…уn) введена функция расстояния р(х,у) по формуле р(х,у)= 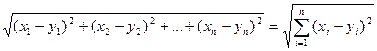
Обозначается n- мерное Евклидово пространство через Еn
Следует отметить, что в этом пространстве могут быть ||x-y||=p(x,y)
Метрические пространства.
Будем говорить, что на множестве Х определена структура метрического пространства, если задана ф-я r(х,у) двух элементов х,уÎХ, удовлетворяющих следующим аксиомам:
1.r(х,у)=0 тогда и только тогда, когда х=у
2.r(х,у)=r(у,х) – аксиома симметрии
3.r(x,z)£r(x,y)+r(x,z)
Ф-я r(х,у) – метрика или ф-я расстояния между точками х,уÎХ.
Т.о. метрическое пространство R=(X,r): ф-я Х с введенной на этом множестве функцией метрикой.
r(х,х)£r(х,у)+r(у,х)
0£2r(х,у)
r(х,у)³0
Примеры:
1).X=R=E1 (множество рациональных чисел)
r(х,у)=|х-у| - удовлетворяет условиям.
2). n-мерным пространством Аn называют множество всевозможных упорядоченных совокупностей n вещественных чисел (х1, х2,…,хn). Каждую упорядоченную совокупность называют точкой n-мерного пространства, а точки х1, х2,…,хn – координатами точки. На Аn, например, метрика:
n
r(х,у) = å((xi-yi)2)1/2
i=1
Линейные пространства.
Множество элементов L, содержащее хотя бы 1 элемент называется линейным или векторным пространством, если выполнены следующие аксиомы:
1. Аксиомы сложения. Для любых двух элементов х,уÎL однозначно определен третий элемент z, называемый их суммой и обозначаемый z=x+y, и справедливы следующие свойства:
а)х+у = у+х
б)(x+y)+z = x+(y+z)
в)$ элемент, называемый нулевым и обозначаемый 0, такой, что для любых хÎL: х+0 = х
г) Для любого хÎХ $ элемент х1, называемый противоположным, такой, что х+х1 = 0
2. Аксиомы умножения на число. Для любого числа а и любого хÎL, определен элемент уÎL, называемый умножением числа а на элемент х и обозначаемый а*х, обладающий следующими свойствами (для любых чисел а, b и любых х,уÎL):
а) a(bx) = ab(x)
б) (a+b)x = ax+bx
в) a(x+y) = ax+ay
г) 1*x = 1
Замечание: если в аксиомах 2 a,bÎR, то линейное пространство называют действительным или вещественным линейным пространством.
Примеры:
1). А1=R. В кач-ве операций сложения – сложение вещественных чисел; в кач-ве операций умножения – умножение вещественных чисел.
2). An
1)а) z = x+y = (x1+y1, x2+y2,…,xn+yn) и так далее все свойства 1) и 2) групп по аналогии.
Нормированные пространства.
F(x) = ||x|| - “норма икс”, ставящая в соответствие любому хÎL (линейн. простран.) вещественное число ||х||, наз. нормой в лин. Пространстве, если она удовлетворяет следующим аксиомам:
1. ||х|| = 0 тогда и только тогда, когда х = 0
2. f(ax) = ||ax|| = ||a||*||x|| = |a|*f(x)
3. f(x+y) = ||x+y|| £ ||x||+||y|| = f(x)+f(y) (x,y - точки)
N – нормированное пространство.
||x||³0
В любом N может быть введена ф-я метрики r(x,y) = ||x-y|
Пример: А1=R=L. F(x) = ||x||=|x| - удовлетворяет условиям.
n-мерное Евклидово пространство.
Координатное пространство Аn называют n-мерным Евклидовым пространством и обозначают Еn, если между двумя его точками ХÎЕn и YÎЕn введена ф-я расстояния r(х,у) по формуле:
n
||x|| = (å(xi-yi)2)1/2
i=1
Еn можно считать нормированным пространством, у которого
||x-y|| = r(x,y)
Неявные функции.
Def Если переменная u, являющаяся по смыслу функцией переменных х1,х2,…,хn задается посредством функций уравнений F(U,X1,x2,…,xn)=0, то говорят, что функция задана неявно.
Частные производные неявно заданной функции вычисляются по формулам:

Рассмотрим совокупность М неявных функций, которые задаются посредством системы М функциональных уравнений:
 (1)
(1)
Пусть функции определены, как решение М функциональных уравнений (2)
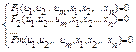 (2)
(2)
Решением системы (2) будет называться совокупность функций, таких что при их подстановки в систему все уравнения этой системы образуются в тождества.
Def Это решение будем называть непрерывным и дифференцируемом в некоторой области D изменения переменных Х1,Х2,…Хn Если каждая из функций U1,U2,…Um непрерывна и дифференцируема в этой области.
 =
= 
Такой определитель называют определителем Якоби или Якобианом.
[T] Система (2) будет разрешима, а решение непрерывно и дифференцируемо, если функция f1,f2,…,fn дифференцируема в окрестности точки Мо,  непрерывна в точке Мо, Якобиан
непрерывна в точке Мо, Якобиан  отличен от 0 и F1=F2=…=Fn в точке Мо
отличен от 0 и F1=F2=…=Fn в точке Мо
Условный экстремум
Задача отыскания экстремума функции аргументы которой удовлетворяют дополнительному условию связи называется задачей отыскания условного экстремума.
Рассмотрим вопрос отыскания экстремума функции z=f(u1,u2,…um,x1,x2,…,xn)
Будем говорить, что эта функция при наличии условий связи 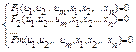 (2) имеет условный максимум (минимум) в точке Мо, координаты которой удовлетворяют этим условиям связи, если существует окрестность точки Мо, для которой значение этой функции в точке Мо является наибольшим (наименьшим) среди всех точек координаты которых удовлетворяют эти условиям связи.
(2) имеет условный максимум (минимум) в точке Мо, координаты которой удовлетворяют этим условиям связи, если существует окрестность точки Мо, для которой значение этой функции в точке Мо является наибольшим (наименьшим) среди всех точек координаты которых удовлетворяют эти условиям связи.
Первый способ решения задачи условного экстремума:
Основная его идея – переход от задачи условного экстремума к задаче безусловного экстремума.
Пусть у функции F1, F2, …Fm дифференцируема в окрестности точки Mо и  непрерывны в окрестности точки Мо. Пусть, кроме того, Якобиан
непрерывны в окрестности точки Мо. Пусть, кроме того, Якобиан  неравен 0 в точке Мо. Тогда система (2) имеет непрерывное дифференцируемое решение
неравен 0 в точке Мо. Тогда система (2) имеет непрерывное дифференцируемое решение  . Подставим это решение в функцию 2: z=
. Подставим это решение в функцию 2: z= 
Метод множителей Лагранжа.
Метод неопределенных множителей Лагранжа. Если система функций уравнений (2) неразрешима, либо ее решение затруднительно для вас, используют более универсальный способ – метод неопределенных множителей Лагранжа. Идея та же – переход от условного экстремума к безусловному.
L=f+l1F1+l2F2+…+lmFm (4)
Функция Лагранжа.
Теперь находим экстремум этой функции. Здесь l1, l2,…ln –множители Лагранжа.
Предположим, что функция дифференцируема
L(u1,u2,…um,x1,x2,…,xn,l1,l2,…ln)
Необходимые условия экстремума:

Эта система содержит u+2m уравнений и u+2m переменных.
Мо(
lо(

Для полученных точек проверяем достаточное условие экстремума.
Признак сравнения.
Пусть для двух рядов си неотрицательными членами 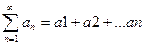 (1)и
(1)и  (2)выполняется неравенство a£b для всех n. Тогда из сходимости ряда (2) следует сходимость ряда (1), а расходимость ряда (1) влечет за собой расходимость ряда (2)
(2)выполняется неравенство a£b для всех n. Тогда из сходимости ряда (2) следует сходимость ряда (1), а расходимость ряда (1) влечет за собой расходимость ряда (2)
Доказательство: Пусть Sn и Sn’ частичные суммы соответственно рядов 1 и 2. Из условия теоремы следует, что Sn£Sn’ Если ряд 2 сходится, то по теореме о необходимом и достаточном условии сходимости ряда последовательность {Sn’} ограничена, значит, монотонная последовательность {Sn} также ограничесна, т.е. она также сходится. Если ряд 1 расходится, то ряд 2 не может сходиться, иначе в силу первой части доказательства будет сходится и ряд 1. ч.т.д.
Замечание: для того, чтобы проверить сходимость-расходимость числового ряда его надо сравнить с заведомо сходящимся рядом *например бесконечно убывающей геометрической прогрессией) или заведомо расходящимся (например с грамоническим рядом или бесконечной программой с q>1)
41.
Признак Даламбера.
Пусть дан ряд åan (111) с положительными членами и существует
n=1
предел lim ((an+1)/(an))=r. Тогда:
n®¥
а) при r<1 ряд сходится; б) при r>1 ряд расходится.
Док-во: а) Пусть r<1 и lim ((an+1)/(an))=r. Докажем, что ряд (111)
n®¥
сходится..По определению предела числовой последовательности для любого e>0 существует номер N такой, что при n³N выполняется неравенство ½(an+1)/(an) - r½< e. Отсюда следует, что r-e< (an+1)/(an)<r+e (1). Т. к. r<1, то e можно взять настолько малым, что будет выполнено неравенство r+e<1. Полагая r+e= q, на основании правого из неравенств (1) имеем (an+1)/(an)<q, или an+1 < anq для n=N, N+1, N+2… (2) Придавая n эти значения, из последнего неравенства получаем aN+1<aNq, aN+2<aN+1q< aNq2, aN+3<aN+2q< aNq3, …….., т.е. члены ряда aN+1+aN+2+ aN+3+… меньше соответствующих членов ряда, составленного из элементов геометрической прогрессии: aNq+ aNq2+ aNq3+… (3). Так как q<1, то ряд (3) сходится. Но ряд (2) получен из данного ряда (111) в результате отбрасывания конечного числа первых членов, след-но, по теореме о свойстве сходящихся рядов ряд (111) сходится.
б) Пусть теперь r>1. Докажем, что ряд (111) расходится. Возьмём e настолько малым, чтобы r-e<1. Тогда при n³N в силу левого из неравенств (1) выполняется неравенство (an+1)/(an)>1 или an+1> an. Таким образом, члены ряда, начиная с некоторого номера N, возрастают с увеличением их номеров, т.е. общий член ряда an не стремится к нулю при n®¥. Следовательно, по теореме о необходимом условии сходимости ряда, ряд (111) сходится.
Замечание. При r=1, как показывают примеры, ряд (111) может как сходиться, так и расходиться. В этом случае необходимо дополнительное исследование ряда с помощью др. признаков.
42. Интегральный признак Коши. ¥
Пусть дан ряд f(1)+f(2)+f(3)+…+f(n)+…= åf(n)
n+1 (222), члены которого являются значениями некоторой функции f(x, положительной, непрерывной и убывающей на +¥
полуинтервале [1, +¥). Тогда, если ò f(x)dx (333) сходится, то сходится и
1
ряд (222).Если же (333)расходится, то и ряд (222) также расходится.
Док-во: Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции y=f(x), с боковых сторон прямыми x=1, x=n, снизу осью Ох. Впишем в эту трапецию и опишем около нее две ступенчатые фигуры, состоящие из прямоугольников с основаниями [1,2], [2,3],…, [n-1,n] и высотами f(1), f(2), f(3),…, f(n-1), f(n). Тогда, принимая во внимание геометрический смысл определённого интеграла, имеем
n
f(2)+f(3)+…+f(n)<òf(x)dx (444)<f(1)+f(2)+…+f(n-1), или, короче,
n 1
Sn-f(1)<òf(x)dx<Sn-f(n).
1 n n
Отсюда получаем: Sn<f(1) + òf(x)dx (1), Sn>f(n) + òf(x)dx (2),где Sn –
1 1
частичные суммы рассматриваемого ряда. Пусть интеграл (444) сходится. Это значит, что существует lim (444)=I.
n®¥ Так как f(x)>0, то последовательность (444) возрастает с увеличением n и ограничена сверху своим пределом: (444)<I. Из неравенства (1) следует, что Sn<f(1) + I, т.е. последовательность частичных сумм {Sn} ряда (222) ограничена. По теореме о необходимом и достаточном условиях сходимости ряда с неотрицательными членами ряд (222) сходится.
Пусть теперь интеграл (333) расходится. В этом случае (444)®+¥ при n®¥ (как монотонно возрастающая неограниченная последовательность). Из неравенства (2) следует, что Sn®+¥ при n®¥, т.е. последовательность частичных сумм {Sn} ряда (222) расходится и, следовательно, ряд расходится.
Степенные ряды.
¥
Ряд вида a0 + a1x +a2x2 +a3x3+…+anxn+…=åanxn (1) называется степенным рядом.
n=0
Числа a0, a1, a2,…,an,… называются коэффициентами степенного ряда.
Придавая х различные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений х, при которых ряд (1) сходится, называется областью его сходимости. Это множество всегда не пусто, т.к. любой степенной ряд сходится при х =0. Очевидно, что частичная сумма Sn (х)= a0 + a1x +…+anxn является функцией переменной х. Поэтому и сумма ряда S также является некоторой функцией переменной х, определённой в области
сходимости ряда:
¥ ¥
S=S(x)= åanxn (или f(x)= åanxn).
n=0 n=0
Теорема Абеля.
1) Если степенной ряд (1) сходится при х=х0 (х0¹ 0), то он сходится, и притом абсолютно, для всех х, удовлетворяющих условию я½ х½<½ х0½.
2) Если ряд (1) расходится при х= х1,то он расходится для всех х, удовлетворяющих условию ½х½<½х1½.
¥
Док-во: 1)т.к. по условию числовой ряд åanx0n сходится, то его общий член anx0n ®0 при
n=0
n®¥, откуда следует, что последовательность { anx0n } ограничена, т.е. существует число M>0 такое, что ½ anx0n ½<M, n =0, 1, 2… (2) Перепишем ряд (1) в виде
a0 + а1х0 (х/х0) + а2х20 (х/х0)2 +…+ аn хn0 (х/х0)n +… (3) и рассмотрим ряд, составленный из абсолютных величин его членов: ½a0½+ ½а1х0½½х/х0½ + ½а2х20½½х/х0½2 +…+ ½аn хn0½½х/х0½n +… (4).
Члены ряда (4) в силу неравенства (2) меньше соответствующих членов ряда
М+ М½х/х0½ + М½х/х0½2 +…+М½х/х0½n +… (5) При ½ х½<½ х0½ ряд (5) представляет собой геометрическую прогрессию со знаменателем q=½х/х0½<1 и, следовательно, сходится.
Т.к. члены ряда (4) меньше соответствующих членов ряда (5) то, по признаку сравнения, ряд (4) также сходится, а это значит, что ряд (1) при ½ х½<½ х0½ сходится абсоютно.
По условию, в точке
x1 ряд (1) расходится. Требуется показать, что он расходится для всех
x, удовлетворяющих условию ½ х½>½ х
1½. Предположим обратное, т.е. допустим, что при некотором значении
х таком, что ½ х½>½ х
1½, ряд (1) сходится. Тогда по только что доказанной первой части теоремы ряд (1) должен сходиться и в точке
х 1, т.к. ½ х
1½<½ х½. Но это противоречит тому, что в точке
х 1 ряд расходится.
Теорема Абеля утверждает, что если х0 – точка сходимости степенного ряда, то во всех точках, расположенных на интервале (-½х0½,½ х0½), этот ряд сходится абсолютно, а если х1 – точка расходимости степенного ряда, то во всех точках, расположенных вне интервала (-½х1½,½ х1½), ряд расходится.
Понятие неопределенного интеграла.
Def Если функция F(x) является первообразной для функции f(x) на промежутке Х, то множество функций {F(x)+C}, где С- произвольная постоянная называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом òf(x)dx=F(x)+C. При этом f(x) называется подынтегральной функцией, f(x)dx- подынтегральным выражением, а переменная х- переменная интегрирования. òf(x)dx- выражает множество всех первообразных для функции f(x) на промежутке Х.
Def Восстановление функции по ее производной или что тоже самое: отыскание неопределенного интеграла называется интегрированием этой функции, т.к. F’(x)=f(x) òF’(x)dx=F(x)+C
Интегрирование- операция обратная дифференцированию и правильность интегрирования определяется следующим образом: мы должны продифференцировать результат и если получили подынтегральную функцию, то операция выполнена верно.
Основные свойства неопределенного интеграла:
1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. (òf(x)dx)’=f(x) и d(òf(x)dx)=f(x)dx Док-во: (òf(x)dx)’=(F(x)+C)’=F’(x)=f(x) и dòf(x)dx=(òf(x)dx)’dx=f(x)dx
2. d(òf(x)dx)=f(x)dx, дифференциал от неопределенного интеграла на промежутке Х равен подынтегральному вырожению.
Док-во: d(òf(x)dx)=d(F(x)+C)=(F(x)+C)’dx=F’(x)dx=f(x)dx
3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е. òdF(x)=F(x)+C. Док-во: т.к. òdF(x)=F’(x)dx, то по определению òF'(x)dx=F(x)+C
4. Постоянный множитель можно вынести из-под знака интеграла, т.е. если k=const¹0, то òkf(x)dx=kòf(x)dx. Док-во: пусть F(x) первообразная для f(x) на промежутке Х, т.е. "xÎX F’(x)=f(x)ÞkF(x) первообразная для kf(x), т.е. (kF(x))’=kF’(x)=kf(x). Из определения следует, что kòf(x)dx=k[F(x)+C]=kF(x)+C1=òkf(x)dx, где С1=кС, ч.т.д.
5. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций отдельно, т.е. ò(f(x)±g(x))dx=òf(x)dx±òg(x)dx. Док-во: пусть F(x) и G(x) являются первообразными для функций f(x) и g(x) на промежутке Х, т.е. "хÎХ F’(x)=f(x), G'(x)=g(x). Тогда функции F(x)±G(x) являются первообразными для функция f(x)±g(x). Следовательно, òf(x)dx±òg(x)dx=(F(x)+C1)±(G(x)+C2)=(F(x)±G(x))+(C1±C2)=[F(x)±G(x)]+C=ò(f(x)±g(x))dx
Это свойство справедливо для любого конечного числа слагаемых.
Методы замены переменной
1. Непосредственное интегрирование.
С помощью табл осн интегралов.
2. Метод подстановки или метод замены переменных.
Достаточно часто введение новой переменой позволяет свести интеграл к табличному
[Т] Пусть функция х=j(t) определена и дифференцируема на некотором промежутке Т и пусть Х- множество значений этой функции, на котором определена функция y=f(x), т.е. на T определена сложная функция y=f[j(t)]. Тогда если на множестве Х функция f(x) имеет первообразную F(x), то справедлива формула òf(x)dx|x=j(t)= òf[j(t)]j’(t)dt. Док-во: Пусть функция F(x) является первообразной для функции f(x) на множестве Х. Рассмотрим на множестве T сложную функцию F[j(t)]. Продифференцируем ее по правилам дифференцирования сложной функции: F’[j(t)]*j’(t)=f’[j(t)]*j’(t)Þ мы получили что эта функция имеет на множестве Т первообразную F[j(t)]. òf[j(t)]*j’(t)dt=F[j(t)]+C=F(x)+C|x=j(t)= òf(x)dx|x=j(t). Получили искомую формулу замены переменных в неопределенном интеграле.
Замечание: При замене переменныхв неопределенном интеграле иногда более удобно задавать не х как функцию t, а задавать t как функцию от х.


 х¹0 такое, чтобы х+
х¹0 такое, чтобы х+ 
 +
+  =f(c)Dx]. Если устремить приращение аргумента к нулю, получим:
=f(c)Dx]. Если устремить приращение аргумента к нулю, получим:  =f(x) или Ф’(х)=f(x), ч т.д. Можно записать, что òf(x)dx=Ф(x)+C=
=f(x) или Ф’(х)=f(x), ч т.д. Можно записать, что òf(x)dx=Ф(x)+C=  DФ(х)=
DФ(х)=  Ф’(x)=
Ф’(x)=  Отсюда следует, что Ф’(x)=f(x)
Отсюда следует, что Ф’(x)=f(x) . Т.е. определенный интеграл от непрерывной функции равн разности значений любой ее первообразной на верхнем и нижнем пределах интегрирования соответственно. Она называется формулой Ньютона-Лейбница.
. Т.е. определенный интеграл от непрерывной функции равн разности значений любой ее первообразной на верхнем и нижнем пределах интегрирования соответственно. Она называется формулой Ньютона-Лейбница. =0, получим: 0=
=0, получим: 0=  , F(a)+C, C=-F(a)
, F(a)+C, C=-F(a) Полагая здесь х=b получим искомую формулу.
Полагая здесь х=b получим искомую формулу.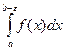 при e®0 называется несобственным интегралом второго рода и обозначается
при e®0 называется несобственным интегралом второго рода и обозначается 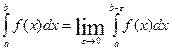 . Если этот предел конечный, то говорят что интеграл существует или сходится, а функцию f(x) называют интегрируемой на промежутке [a,b), если предела нет или он бесконечен, то говорят что интеграл расходится. Аналогично, если особой является точка х=а, то несобственных интеграл второго рода определяется как
. Если этот предел конечный, то говорят что интеграл существует или сходится, а функцию f(x) называют интегрируемой на промежутке [a,b), если предела нет или он бесконечен, то говорят что интеграл расходится. Аналогично, если особой является точка х=а, то несобственных интеграл второго рода определяется как 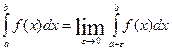 Если функция f(x) не ограничена в окрестности некоторой внутренней точки сÎ[a,b], то по определению полагают
Если функция f(x) не ограничена в окрестности некоторой внутренней точки сÎ[a,b], то по определению полагают 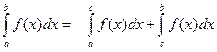 , где несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам предыдущим. Если а и b особые точки, т.е. функция f(x) ограничена и интегрируема на интервале (a,b), то несобственный интеграл второго рода определяется в виде суммы
, где несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам предыдущим. Если а и b особые точки, т.е. функция f(x) ограничена и интегрируема на интервале (a,b), то несобственный интеграл второго рода определяется в виде суммы 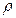 (x,y)=0 тогда и только тогда, когда x=y
(x,y)=0 тогда и только тогда, когда x=y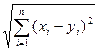
 ax при этом справедливы следующие свойства:
ax при этом справедливы следующие свойства: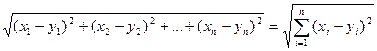

 (1)
(1)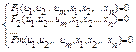 (2)
(2) =
= 
 непрерывна в точке Мо, Якобиан
непрерывна в точке Мо, Якобиан  отличен от 0 и F1=F2=…=Fn в точке Мо
отличен от 0 и F1=F2=…=Fn в точке Мо непрерывны в окрестности точки Мо. Пусть, кроме того, Якобиан
непрерывны в окрестности точки Мо. Пусть, кроме того, Якобиан 



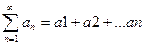 (1)и
(1)и  (2)выполняется неравенство a£b для всех n. Тогда из сходимости ряда (2) следует сходимость ряда (1), а расходимость ряда (1) влечет за собой расходимость ряда (2)
(2)выполняется неравенство a£b для всех n. Тогда из сходимости ряда (2) следует сходимость ряда (1), а расходимость ряда (1) влечет за собой расходимость ряда (2)