В прикладных задачах теории вероятностей часто возникает необходимость оценки значения реализации  одной случайной величины
одной случайной величины 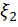 (ненаблюдаемой) по значению реализации
(ненаблюдаемой) по значению реализации  (по выборочному значению) другой случайной величины
(по выборочному значению) другой случайной величины 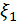 (наблюдаемой). Оценка имеет смысл только в том случае, когда случайные величины
(наблюдаемой). Оценка имеет смысл только в том случае, когда случайные величины 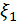 и
и 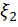 статистически зависимы, т.е. закон распределения случайной величины
статистически зависимы, т.е. закон распределения случайной величины 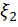 зависит от значения реализации
зависит от значения реализации  случайной величины
случайной величины 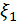 (
( ). Поскольку закон распределения
). Поскольку закон распределения 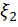 полностью определяется комплексом условий D эксперимента, то величина
полностью определяется комплексом условий D эксперимента, то величина  должна быть параметром этого комплекса условий или так или иначе влиять на него. Условную плотность вероятностей
должна быть параметром этого комплекса условий или так или иначе влиять на него. Условную плотность вероятностей  можно рассматривать как формальную математическую модель зависимости, которая отражает влияние значения
можно рассматривать как формальную математическую модель зависимости, которая отражает влияние значения  на вероятность появления
на вероятность появления  через комплекс условий D.
через комплекс условий D.
В качестве оценки значения  выбирается значение
выбирается значение  некоторой функции
некоторой функции  , вид которой определяет качество оценки. При отдельном наблюдении ошибка равна
, вид которой определяет качество оценки. При отдельном наблюдении ошибка равна  . При многократном наблюдении одного и того же значения
. При многократном наблюдении одного и того же значения  случайная величина
случайная величина 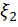 , закон распределения которой
, закон распределения которой  зависит от
зависит от  , будет принимать разные значения, то есть ошибка
, будет принимать разные значения, то есть ошибка  будет случайной величиной, средний квадрат
будет случайной величиной, средний квадрат  которой можно выбрать в качестве критерия качества оценки:
которой можно выбрать в качестве критерия качества оценки:
 (1.1)
(1.1)
Поскольку среднеквадратическая ошибка  зависит от значения
зависит от значения  , то ее можно назвать условной. В качестве критерия чаще используется безусловная среднеквадратическая ошибка, которая получается в результате статистического усреднения
, то ее можно назвать условной. В качестве критерия чаще используется безусловная среднеквадратическая ошибка, которая получается в результате статистического усреднения  по всем значениям
по всем значениям  :
:
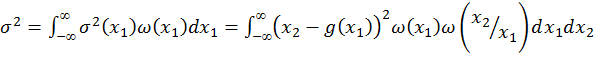 ,
,
причем  =
=  .
.
Докажем, что  минимальна, когда функция
минимальна, когда функция 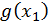 совпадает с условным средним значением случайной величины
совпадает с условным средним значением случайной величины 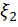 :
:

Поскольку  , то
, то  будет минимальна, если
будет минимальна, если  будет минимальна при каждом
будет минимальна при каждом  . Преобразуя (1.1) при заданном значении
. Преобразуя (1.1) при заданном значении  , получим:
, получим:
 =
=  =
=
 +
+  +2
+2  (
( ).
).
Сомножитель  =
=  =0, и поэтому третье слагаемое равно нулю. Поскольку от
=0, и поэтому третье слагаемое равно нулю. Поскольку от 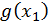 зависит только второе слагаемое и оно неотрицательно, то минимум суммы достигается при
зависит только второе слагаемое и оно неотрицательно, то минимум суммы достигается при  , т.е., когда второй член равен 0.
, т.е., когда второй член равен 0.
Условное среднее значение случайной величины 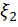 при
при 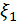 =
=  , (
, ( ), рассматриваемое как функция переменного
), рассматриваемое как функция переменного  , называется функцией регрессии
, называется функцией регрессии 
Функция регрессии отражает зависимость одного из параметров (среднего значения) закона распределения случайной величины 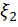 от значения
от значения  (реализация) случайной величины
(реализация) случайной величины 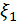 . Если зависимость среднего значения от
. Если зависимость среднего значения от  отсутствует, то это еще не значит, что случайные величины
отсутствует, то это еще не значит, что случайные величины  и
и 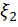 независимы – в общем случае от
независимы – в общем случае от  может зависеть не только среднее значение, но и другие параметры распределения. Если же случайные величины
может зависеть не только среднее значение, но и другие параметры распределения. Если же случайные величины 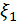 и
и 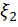 независимы, то и каждый параметр распределения
независимы, то и каждый параметр распределения 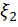 не будет зависеть от
не будет зависеть от  , то есть форма функции распределения
, то есть форма функции распределения 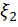 не будет зависеть от
не будет зависеть от 
Линейная функция регрессия.
В некоторых случаях вводится ограничение на вид возможных функций 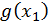 , например, ограничиваются классом линейных функций
, например, ограничиваются классом линейных функций 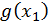 , которые записываются в виде
, которые записываются в виде 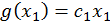 +
+ 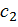 . Выбор оптимальной функции из этого класса, т.е. той, которая дает оценку с минимальной среднеквадратической ошибкой, сводится к определению коэффициентов
. Выбор оптимальной функции из этого класса, т.е. той, которая дает оценку с минимальной среднеквадратической ошибкой, сводится к определению коэффициентов 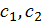 .
.
Функция 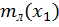 =
= 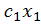 +
+ 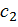 , для которой среднеквадратическая ошибка
, для которой среднеквадратическая ошибка
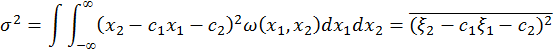
минимальна, называется функцией линейной регрессии, а соответствующие коэффициенты 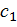 и
и 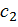 – коэффициентами регрессии.
– коэффициентами регрессии.
Обозначив через 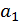 и
и 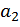 средние значения случайных величин
средние значения случайных величин 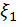 и
и 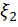 , коэффициенты регрессии можно определить, если сделать следующие тождественные преобразования:
, коэффициенты регрессии можно определить, если сделать следующие тождественные преобразования:
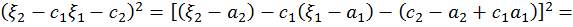
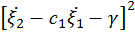 , где
, где 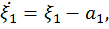
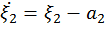 ,
, 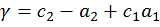 ,
, 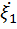 и
и 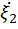 - центрированные случайные величины.
- центрированные случайные величины.
Тогда 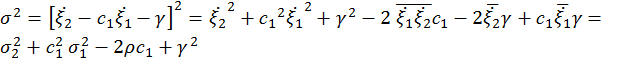 , (1.2)
, (1.2)
где 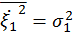 и
и 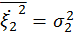 по определению дисперсии случайных величин
по определению дисперсии случайных величин 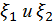 ,
, 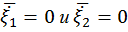 как среднее значение от центрированных случайных величин.
как среднее значение от центрированных случайных величин.
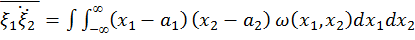 =
= 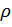 –
–
среднее от произведения двух центрированных случайных величин 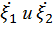 называется корреляцией между этими случайными величинами. Иногда удобнее использовать коэффициент корреляции r =
называется корреляцией между этими случайными величинами. Иногда удобнее использовать коэффициент корреляции r = 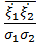 =
= 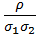 , который определяется как среднее значение от произведения центрированных и нормированных случайных величин
, который определяется как среднее значение от произведения центрированных и нормированных случайных величин 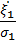 и
и 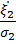 .
.
С учетом введенных обозначений можно произвести следующие тождественные преобразования выражения (1.2):

Отсюда следует, что минимум среднеквадратической ошибки, равный 
достигается при тех значениях  , при которых последние два слагаемых (неотрицательные) равны нулю:
, при которых последние два слагаемых (неотрицательные) равны нулю:


Решая эту систему уравнений, получим:
 ;
; 
Соответствующая функция линейной регрессии имеет вид:
 =
=  (
(  ) (1.3)
) (1.3)
C целью наглядности геометрической интерпретации последнее равенство можно представить в виде:
 =
=  (
(  ) (1.4)
) (1.4)
или
 (1.5)
(1.5)
Для построения функции линейной регрессии достаточно знать только средние значения, дисперсии случайных величин 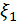 ,
,  и их коэффициент корреляции, который равен тангенсу угла наклона прямой, определяемой выражением (1.5), если по осям откладывать соответственно значения
и их коэффициент корреляции, который равен тангенсу угла наклона прямой, определяемой выражением (1.5), если по осям откладывать соответственно значения  и
и  .
.

Рис. 1.19. Линейная функция регрессии, tg  = r
= r
Следует отметить, что в общем случае, то есть для произвольной плотности  . Функция линейной регрессии (1.9) может не совпадать с действительной функцией регрессии m(
. Функция линейной регрессии (1.9) может не совпадать с действительной функцией регрессии m( ), поскольку условное среднее m(
), поскольку условное среднее m( ) может быть нелинейной функцией.
) может быть нелинейной функцией.
Поэтому, если r=0, то говорят, что между  и
и 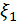 отсутствует линейная зависимость, но это еще не значит, что между условным средним значением случайной величины
отсутствует линейная зависимость, но это еще не значит, что между условным средним значением случайной величины 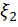 и значением
и значением  вообще отсутствует какая-либо зависимость.
вообще отсутствует какая-либо зависимость.
Пример. Рассмотрим классическую задачу измерения физической величины. До измерения физической величины обычно располагают некоторыми сведениями о ее значении, например, может быть известна область ее возможных значений и степень ожидания того или другого значения, которая характеризуется вероятностью. В рамках теории вероятностей измеряемая величина рассматривается как реализация случайной величины  (ненаблюдаемой), априорная (до измерения) неопределенность которой ограничивается видом ее закона распределения
(ненаблюдаемой), априорная (до измерения) неопределенность которой ограничивается видом ее закона распределения  с дисперсией
с дисперсией  и средним значением, равным
и средним значением, равным  Результат измерения рассматривается как реализация случайной величины (наблюдаемой)
Результат измерения рассматривается как реализация случайной величины (наблюдаемой)  , где Δ – ошибка измерения с нулевым средним значением (Δ=0), которая представляет собой сумму двух независимых случайных величин
, где Δ – ошибка измерения с нулевым средним значением (Δ=0), которая представляет собой сумму двух независимых случайных величин  и Δ и имеет дисперсию
и Δ и имеет дисперсию

И среднее значение  =
=  =
= 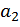 .
.
Тогда корреляция между случайными величинами  и
и 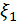 равна
равна
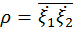 =
= 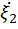 (
(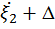 )=
)= 
где 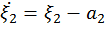 ,
,  = 0.
= 0.
Коэффициент корреляции
r =  =
= 
а равенство (1.9) запишется в виде

или
 =
=  (
( ).
).
Отсюда следует, что эффективная оценка  значения измеряемой физической величины не совпадает с результатом измерения
значения измеряемой физической величины не совпадает с результатом измерения 
Если дисперсия 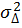 ошибки измерения(неопределенность результата измерения или апостериорная неопределенность) много меньше дисперсии
ошибки измерения(неопределенность результата измерения или апостериорная неопределенность) много меньше дисперсии  , которая характеризует априорную неопределенность, то
, которая характеризует априорную неопределенность, то 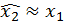 , а при
, а при 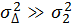 оценка
оценка  =
= 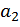 , т.е. в этом случае результат измерения
, т.е. в этом случае результат измерения  практически не несет информации о значении физической величины в дополнение к тому, что было о ней известно до измерения.
практически не несет информации о значении физической величины в дополнение к тому, что было о ней известно до измерения.
Минимальная среднеквадратическая ошибка равна

Из этого равенства следует, что в случае полного отсутствия априорных сведений об измеряемой величине  и, следовательно,
и, следовательно,  . Когда же значение измеряемой величины заранее известно (
. Когда же значение измеряемой величины заранее известно ( ,
,  нет необходимости производить измерение. Если дисперсия
нет необходимости производить измерение. Если дисперсия 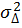 =0 (абсолютно точное измерение), то,
=0 (абсолютно точное измерение), то,  , т.е. всю необходимую информацию о значении измеряемой величины доставляет результат измерения и поэтому априорными сведениями можно пренебречь.
, т.е. всю необходимую информацию о значении измеряемой величины доставляет результат измерения и поэтому априорными сведениями можно пренебречь.
Если  , то
, то  , то есть результат измерения не доставляет какой-либо информации и неопределенность измеряемой величины определяется априорной дисперсией
, то есть результат измерения не доставляет какой-либо информации и неопределенность измеряемой величины определяется априорной дисперсией  .
.
Интересно сравнить эту задачу с задачей предсказания результата измерения по известному значению измеряемой величины. По отношению к предыдущей задаче наблюдаемая и ненаблюдаемая величины поменяются местами и равенство (1.9) примет вид
 ,
,
причем 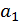 =
= 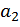 . Коэффициент корреляции не изменится и будет равен r=
. Коэффициент корреляции не изменится и будет равен r= 
Отсюда следует, что  =
=  и ошибка предсказания
и ошибка предсказания
 .
.
Таким образом, чтобы эффективно предсказать результат измерения, в качестве его оценки всегда следует брать истинное значение измеряемой величины. В заключение следует отметить, что при оценке ненаблюдаемой величины по критерию среднеквадратической ошибки используются не все априорные сведения, содержащиеся в ее законе распределения, а только ее дисперсия и среднее.



 одной случайной величины
одной случайной величины 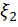 (ненаблюдаемой) по значению реализации
(ненаблюдаемой) по значению реализации  (по выборочному значению) другой случайной величины
(по выборочному значению) другой случайной величины 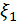 (наблюдаемой). Оценка имеет смысл только в том случае, когда случайные величины
(наблюдаемой). Оценка имеет смысл только в том случае, когда случайные величины  ). Поскольку закон распределения
). Поскольку закон распределения  можно рассматривать как формальную математическую модель зависимости, которая отражает влияние значения
можно рассматривать как формальную математическую модель зависимости, которая отражает влияние значения  некоторой функции
некоторой функции  , вид которой определяет качество оценки. При отдельном наблюдении ошибка равна
, вид которой определяет качество оценки. При отдельном наблюдении ошибка равна  . При многократном наблюдении одного и того же значения
. При многократном наблюдении одного и того же значения  зависит от
зависит от  будет случайной величиной, средний квадрат
будет случайной величиной, средний квадрат  которой можно выбрать в качестве критерия качества оценки:
которой можно выбрать в качестве критерия качества оценки: (1.1)
(1.1) зависит от значения
зависит от значения 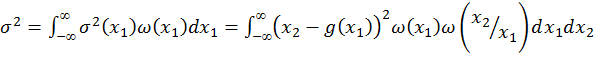 ,
, =
=  .
. минимальна, когда функция
минимальна, когда функция 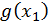 совпадает с условным средним значением случайной величины
совпадает с условным средним значением случайной величины 
 , то
, то  будет минимальна, если
будет минимальна, если  =
=  =
= +
+  +2
+2  (
( ).
). =
=  =0, и поэтому третье слагаемое равно нулю. Поскольку от
=0, и поэтому третье слагаемое равно нулю. Поскольку от  , т.е., когда второй член равен 0.
, т.е., когда второй член равен 0. ), рассматриваемое как функция переменного
), рассматриваемое как функция переменного 
 (реализация) случайной величины
(реализация) случайной величины  и
и 
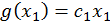 +
+ 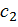 . Выбор оптимальной функции из этого класса, т.е. той, которая дает оценку с минимальной среднеквадратической ошибкой, сводится к определению коэффициентов
. Выбор оптимальной функции из этого класса, т.е. той, которая дает оценку с минимальной среднеквадратической ошибкой, сводится к определению коэффициентов 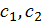 .
.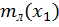 =
= 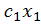 +
+ 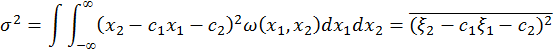
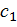 и
и 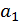 и
и 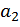 средние значения случайных величин
средние значения случайных величин 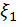 и
и 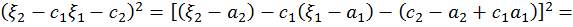
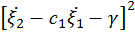 , где
, где 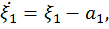
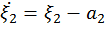 ,
, 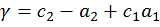 ,
, 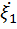 и
и 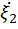 - центрированные случайные величины.
- центрированные случайные величины.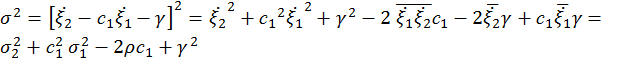 , (1.2)
, (1.2)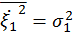 и
и 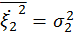 по определению дисперсии случайных величин
по определению дисперсии случайных величин 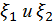 ,
, 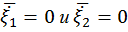 как среднее значение от центрированных случайных величин.
как среднее значение от центрированных случайных величин.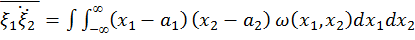 =
= 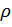 –
–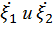 называется корреляцией между этими случайными величинами. Иногда удобнее использовать коэффициент корреляции r =
называется корреляцией между этими случайными величинами. Иногда удобнее использовать коэффициент корреляции r = 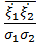 =
= 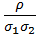 , который определяется как среднее значение от произведения центрированных и нормированных случайных величин
, который определяется как среднее значение от произведения центрированных и нормированных случайных величин 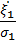 и
и 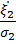 .
.

 , при которых последние два слагаемых (неотрицательные) равны нулю:
, при которых последние два слагаемых (неотрицательные) равны нулю:

 ;
; 
 =
=  (
(  ) (1.3)
) (1.3) =
=  (
(  (1.5)
(1.5) и их коэффициент корреляции, который равен тангенсу угла наклона прямой, определяемой выражением (1.5), если по осям откладывать соответственно значения
и их коэффициент корреляции, который равен тангенсу угла наклона прямой, определяемой выражением (1.5), если по осям откладывать соответственно значения  и
и  .
.
 = r
= r . Функция линейной регрессии (1.9) может не совпадать с действительной функцией регрессии m(
. Функция линейной регрессии (1.9) может не совпадать с действительной функцией регрессии m( с дисперсией
с дисперсией  и средним значением, равным
и средним значением, равным  Результат измерения рассматривается как реализация случайной величины (наблюдаемой)
Результат измерения рассматривается как реализация случайной величины (наблюдаемой)  , где Δ – ошибка измерения с нулевым средним значением (Δ=0), которая представляет собой сумму двух независимых случайных величин
, где Δ – ошибка измерения с нулевым средним значением (Δ=0), которая представляет собой сумму двух независимых случайных величин 
 =
=  =
= 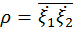 =
= 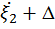 )=
)= 
 = 0.
= 0. =
= 

 (
( ).
).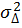 ошибки измерения(неопределенность результата измерения или апостериорная неопределенность) много меньше дисперсии
ошибки измерения(неопределенность результата измерения или апостериорная неопределенность) много меньше дисперсии 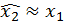 , а при
, а при 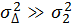 оценка
оценка 
 и, следовательно,
и, следовательно,  . Когда же значение измеряемой величины заранее известно (
. Когда же значение измеряемой величины заранее известно ( ,
,  нет необходимости производить измерение. Если дисперсия
нет необходимости производить измерение. Если дисперсия  , т.е. всю необходимую информацию о значении измеряемой величины доставляет результат измерения и поэтому априорными сведениями можно пренебречь.
, т.е. всю необходимую информацию о значении измеряемой величины доставляет результат измерения и поэтому априорными сведениями можно пренебречь. , то
, то  , то есть результат измерения не доставляет какой-либо информации и неопределенность измеряемой величины определяется априорной дисперсией
, то есть результат измерения не доставляет какой-либо информации и неопределенность измеряемой величины определяется априорной дисперсией  ,
,
 =
=  .
.

