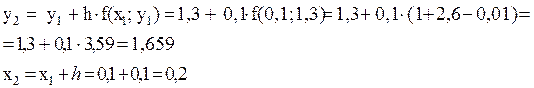7.2. Метод трапеций
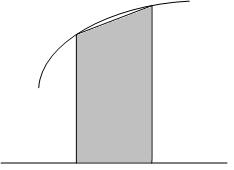
В данном методе (дуга f(x) заменяется хордой CD) (рис. 7.6).
Рис. 7.6. Оценка элементарной площади Si трапецией
Из рисунка 7.6. видно, что 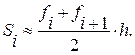
Отсюда:
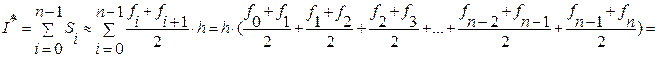
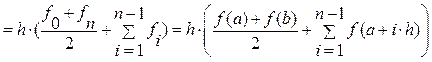 (7.7)
(7.7)
Погрешность формулы трапеций пропорциональна квадрату шага h 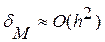 , т. е. формулы центральных прямоугольников и трапеций имеют близкую точность.
, т. е. формулы центральных прямоугольников и трапеций имеют близкую точность.
Знак погрешности легко объяснить по геометрической иллюстрации применения формулы.
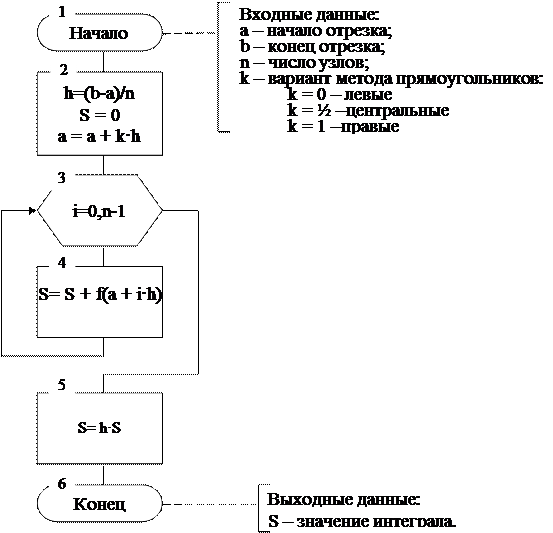
Блок-схема алгоритма вычисления определенного интеграла методом трапеций
Метод Симпсона
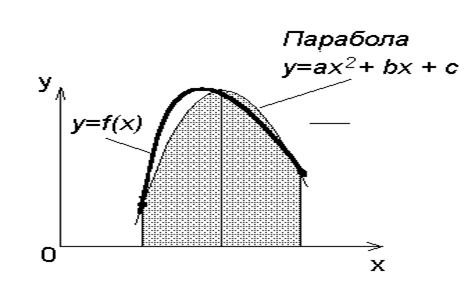
На каждом элементарном отрезке подынтегральная функция f(x) заменяется квадратичной параболой, построенной по трем точкам: концам элементарного отрезка (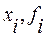 ), (
), (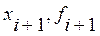 ) и его середине (
) и его середине (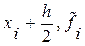 ).
).
Площадь полученной криволинейной трапеции служит оценкой элементарной площади Si:
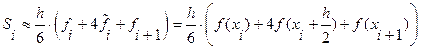 .
.
Тогда значение интеграла:
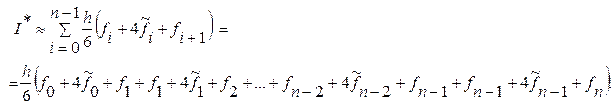
Преобразуем данную формулу:
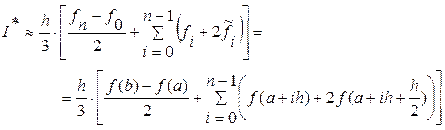 (7.8)
(7.8)
Формула Симпсона имеет высокую точность, так как погрешность метода dм = О(h3).
Блок-схема алгоритма вычисления определенного интеграла методом Симпсона.
Точность и сходимость методов прямоугольников, трапеций, Симпсона
Формулы для оценки погрешности численного интегрирования методом:
1) прямоугольников:
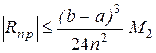 ; (7.9)
; (7.9)
2) трапеций:
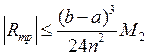 ; (7.10)
; (7.10)
3) Симпсона:
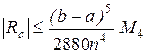 , (7.11)
, (7.11)
где 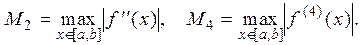
Формула Симпсона обладает повышенной точностью, т. к.:
1) она оказывается точной для 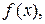 являющихся полиномами до третьей степени включительно, т. к. для этих случаев производная четвертого порядка равна нулю;
являющихся полиномами до третьей степени включительно, т. к. для этих случаев производная четвертого порядка равна нулю;
2) для достижения той же точности, что и в формуле трапеций, в формуле Симпсона можно брать меньшее число 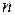 отрезков разбиения.
отрезков разбиения.
Задание
Вычислить определенный интеграл методами:
1) трапеций;
2) прямоугольников;
3) Симпсона.
Варианты заданий:
| № Вар.
| Подынтег-
ральная
функция
| Интервал
интег-
рирования
[a, b]
| Кол-во
частей
разбие-ния:
n1, n2, n3
| Первообразная функция
F(x)
|
|
| 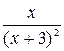
| [2;5]
| 40, 80, 200
| 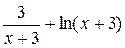
|
|
| 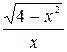
| [3;7]
| 80, 150, 400
| 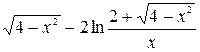
|
|
| 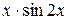
| [0,9;3,1]
| 20, 100, 500
| 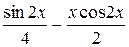
|
|
| 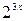
| [0,2; 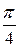 ] ]
| 50, 180, 400
| 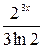
|
|
| 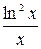
| [0,8;1,9]
| 50, 200, 1000
| 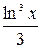
|
|
| 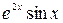
| [1;5]
| 30, 500, 1200
| 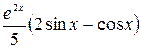
|
|
| 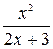
| [2; 6]
| 100, 300, 2000
| 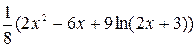
|
|
| 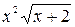
| [1;3]
| 50, 400, 2500
| 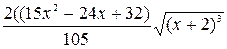
|
|
| 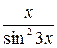
| [0,8;4,5]
| 25,150, 1000
| 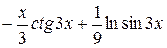
|
|
| 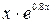
| [2;3]
| 40, 300, 2000
| 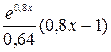
|
|
| 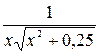
| [1,7;3,2]
| 50, 250, 500
| -2·1n(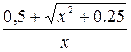 ) )
|
|
| 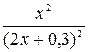
| [2,1;4,2]
| 80, 300, 2000
| 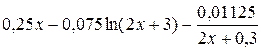
|
|
| 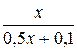
| [3;5]
| 50, 500, 4000
| 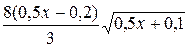
|
|
| 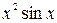
| [2;3,1]
| 40, 200, 5000
| 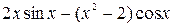
|
|
| 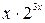
| [2;4]
| 60, 180, 3500
| 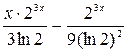
|
7.5. Контрольные вопросы
1. Объяснить геометрический смысл определенного интеграла.
2. Какой зависимостью связан шаг интегрирования с количеством интервалов?
3. Какой из методов вычисления определенного интеграла является самым точным и как это определяется?
Лабораторная работа № 8. РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
Дифференциальные уравнения
Общий вид дифференциального уравнения 1-го порядка:
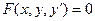 . (8.1)
. (8.1)
Если это уравнение разрешимо относительно 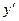 , то
, то
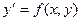 или
или 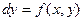 (8.2)
(8.2)
Общим решением уравнения (8.1) называется функция
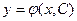 (8.3)
(8.3)
от x и произвольной постоянной С, обращающая это уравнение в тождество.
Частным решением уравнения (8.1) называется решение, полученное из общего решения (8.3) при фиксированном значении С:
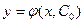 , (8.4)
, (8.4)
где 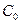 – фиксированное число.
– фиксированное число.
Задача Коши. Найти решение 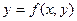 дифференциального уравнения (8.1), удовлетворяющее заданным начальным условиям:
дифференциального уравнения (8.1), удовлетворяющее заданным начальным условиям: 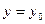 при
при 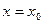 . Другими словами, найти интегральную кривую уравнения (8.1), проходящую через данную точку
. Другими словами, найти интегральную кривую уравнения (8.1), проходящую через данную точку 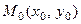 .
.
8. 1. Метод Эйлера (метод Рунге – Кутта 1-го порядка)
Разобъем [a, b] на n равных частей – элементарных отрезков, x 0, x 1, …, x n будем называть узлами сетки, h = (b – a) / n - шаг сетки.
Очевидно, что 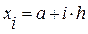 ,
, 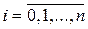 ;
; 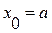 ,
, 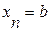 .
.
Заменим в уравнении (8.1) 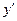 в точке xi ее приближенной оценкой – отношением приращений (это следует из определения производной):
в точке xi ее приближенной оценкой – отношением приращений (это следует из определения производной):
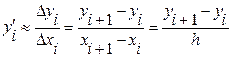 .
.
Тогда получаем:
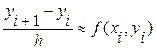
Отсюда формула Эйлера:
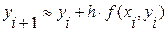 (8.5)
(8.5)
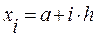 ,
, 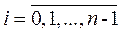 – номер узла
– номер узла
Зная y0 в точке x0 (начальное условие) можно найти y1, затем, используя уже известные значения x1 и y1, вычислить x2 и y2 и так далее.
Если функция 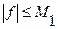 ,
, 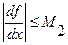 ,
, 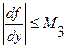 для
для 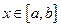 ,
, 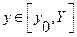 , то имеет место неравенство:
, то имеет место неравенство:
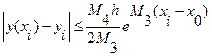 ,
,
где 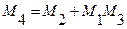 ,
, 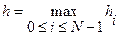 .
.
Оценка имеет лишь теоретическое значение. На практике чаще всего пользуются двойным пересчетом на ЭВМ: расчет на отрезке 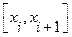 (повторяют с шагом
(повторяют с шагом 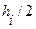 ) и погрешность более точного решения
) и погрешность более точного решения 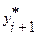 (при шаге
(при шаге 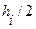 ) оценивают по формуле:
) оценивают по формуле:
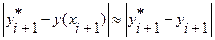 .
.
Рассмотрим геометрическую иллюстрацию метода Эйлера (рис. 8.1). В координатах (x, y) отобразим известные данные: отрезок [a, b] на оси Х и начальное условие y 0 – точка А с координатами (a, y 0). Отрезок [a,b] разобьем на n равных частей, получим узлы равномерной сетки a = x0, x1, x2, …, xn = b. Вычислим значения первой производной искомой функции в точке А, используя координату этой точки и исходное уравнение (8.3):
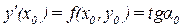
Полученное значение позволяет построить касательную к искомой функции в точке А. Эту касательную можно использовать для вычисления приближенного значения искомой функции в новом узле х1 (кривую y(x) заменяем отрезком АВ на элементарном отрезке [ x0, x1 ]).
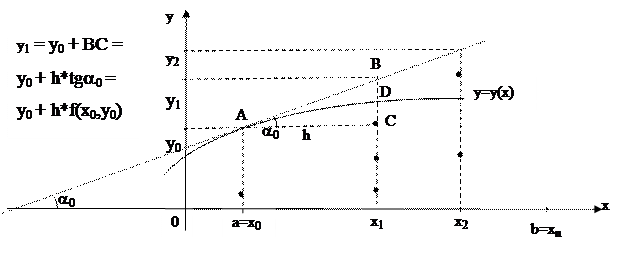
Рис. 8.1. Геометрическая иллюстрация метода Эйлера.
Зная (x1,y1), можно аналогично получить новую точку (x2,y2) и т. д.
Из геометрической иллюстрации следует, что:
1. На каждом шаге есть погрешность (на рис. 8.1 это отрезок BD).
Погрешность тем больше, чем больше шаг.
2. Ошибка может накапливаться.
Формула Эйлера (8.3) имеет погрешность метода 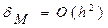 .
.
Для практического выбора h с целью обеспечения заданной точности решения задачи e применяется следующий прием.
Выполняются 2 расчета: с n и 2 n узлами. Если полученные значения функции во всех узлах отличаются не более чем на e, задача считается решенной. Если нет, число узлов вновь удваивают и опять сравнивают полученные значения функций.
Таким образом, расчет продолжается до достижения условия
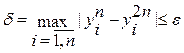 . (8.6)
. (8.6)
Значение n может достигать большой величины – более 1000. Чтобы не печатать столько значений функции, в алгоритме решения ОДУ методом Эйлера нужно предусмотреть печать не всех рассчитанных значений, а только части их, например, 10-ти значений, распределенных равномерно по всему отрезку.
Пример 1. Дано уравнение 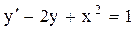 .
.
Найти решение для отрезка [0; 1], если y(0) = 1.
Выберем n = 10, тогда шаг h =(1-0)/10 = 0,1.
Запишем уравнение в каноническом виде 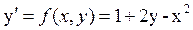
Начальная точка x0 = 0, y0 = 1.
Вычислим первую точку
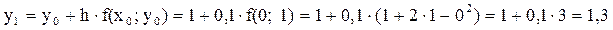 x1 = x0 + h = 0 + 0,1 = 0,1
x1 = x0 + h = 0 + 0,1 = 0,1
Вычислим вторую точку:
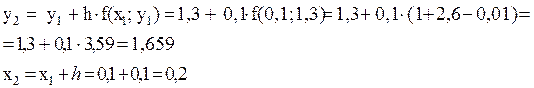
Аналогично нужно вычислить еще восемь точек (т. к. выбрано n=10).




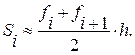
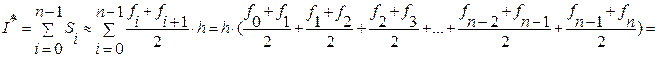
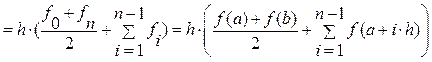 (7.7)
(7.7)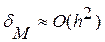 , т. е. формулы центральных прямоугольников и трапеций имеют близкую точность.
, т. е. формулы центральных прямоугольников и трапеций имеют близкую точность.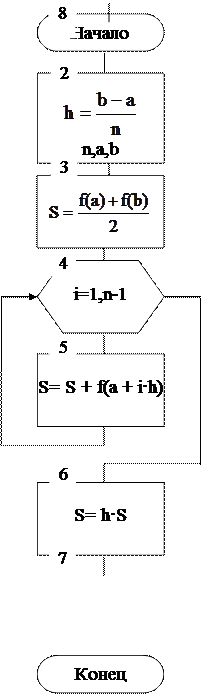


 ), (
), ( ) и его середине (
) и его середине (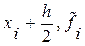 ).
).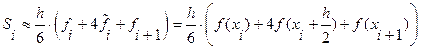 .
.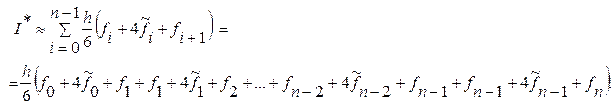
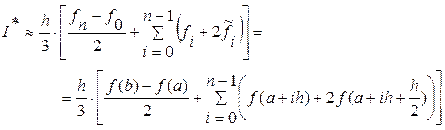 (7.8)
(7.8)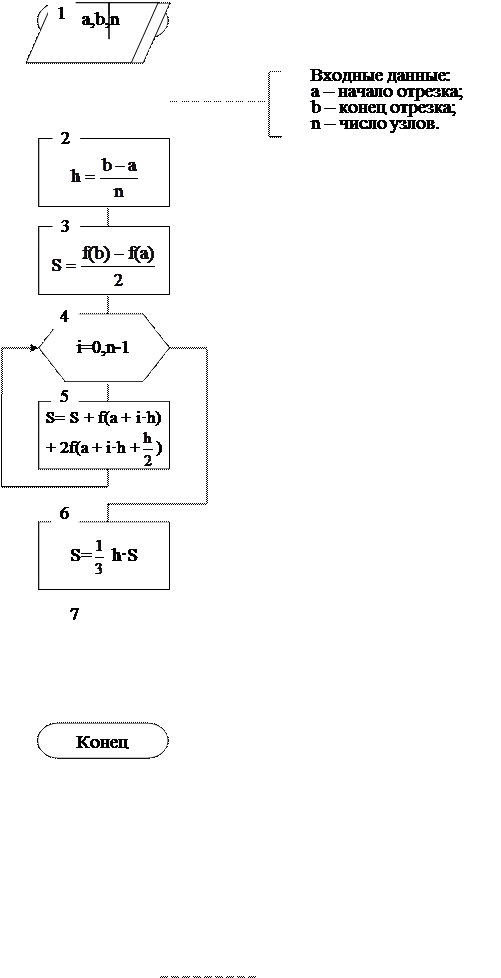
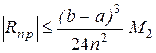 ; (7.9)
; (7.9)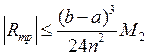 ; (7.10)
; (7.10)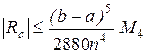 , (7.11)
, (7.11)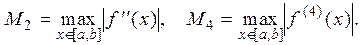
 являющихся полиномами до третьей степени включительно, т. к. для этих случаев производная четвертого порядка равна нулю;
являющихся полиномами до третьей степени включительно, т. к. для этих случаев производная четвертого порядка равна нулю; отрезков разбиения.
отрезков разбиения.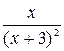
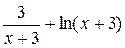
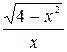
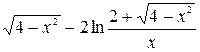
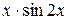
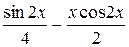
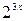
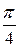 ]
]
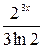
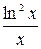
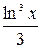
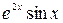
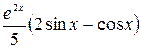
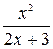
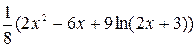
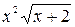
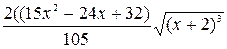
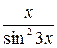
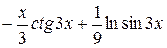
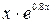
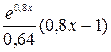
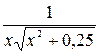
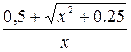 )
)
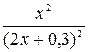
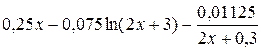
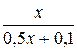
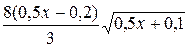
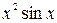
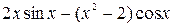
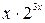
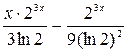
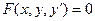 . (8.1)
. (8.1)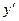 , то
, то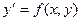 или
или 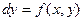 (8.2)
(8.2)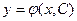 (8.3)
(8.3)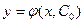 , (8.4)
, (8.4)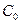 – фиксированное число.
– фиксированное число.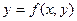 дифференциального уравнения (8.1), удовлетворяющее заданным начальным условиям:
дифференциального уравнения (8.1), удовлетворяющее заданным начальным условиям: 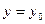 при
при 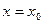 . Другими словами, найти интегральную кривую уравнения (8.1), проходящую через данную точку
. Другими словами, найти интегральную кривую уравнения (8.1), проходящую через данную точку 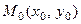 .
.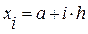 ,
, 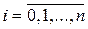 ;
; 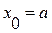 ,
, 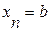 .
.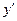 в точке xi ее приближенной оценкой – отношением приращений (это следует из определения производной):
в точке xi ее приближенной оценкой – отношением приращений (это следует из определения производной):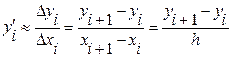 .
.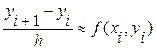
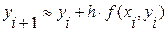 (8.5)
(8.5)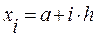 ,
, 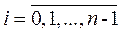 – номер узла
– номер узла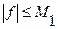 ,
, 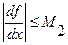 ,
, 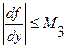 для
для 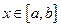 ,
, 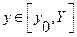 , то имеет место неравенство:
, то имеет место неравенство: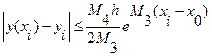 ,
,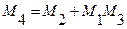 ,
, 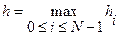 .
.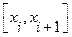 (повторяют с шагом
(повторяют с шагом 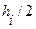 ) и погрешность более точного решения
) и погрешность более точного решения 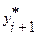 (при шаге
(при шаге 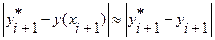 .
.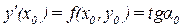

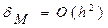 .
.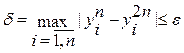 . (8.6)
. (8.6)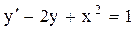 .
.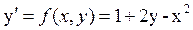
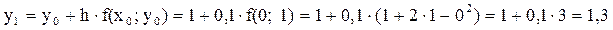 x1 = x0 + h = 0 + 0,1 = 0,1
x1 = x0 + h = 0 + 0,1 = 0,1