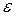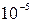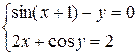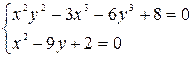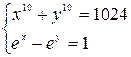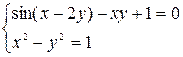
Линейная интерполяция
Линейная интерполяция состоит в том, что заданные точки 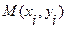
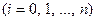 соединяются прямолинейными отрезками и функция
соединяются прямолинейными отрезками и функция 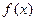 приближается к ломаной с вершинами в данных точках. Поскольку имеется n интервалов
приближается к ломаной с вершинами в данных точках. Поскольку имеется n интервалов 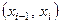 , то для каждого из них в качестве уравнения интерполяционного полинома используется уравнение прямой, проходящей через две точки. В частности для i -го интервала можно записать уравнение прямой, проходящей через точки
, то для каждого из них в качестве уравнения интерполяционного полинома используется уравнение прямой, проходящей через две точки. В частности для i -го интервала можно записать уравнение прямой, проходящей через точки 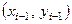 и
и 
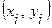 , в виде:
, в виде:
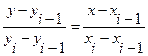
Отсюда
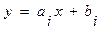 ,
, 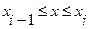 , (4.5)
, (4.5)
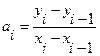 ,
, 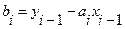 .
.
Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу (4.5) и найти приближенное значение функции в этой точке.
Блок-схема для линейной интерполяции

4.3. Задание
Решить задания методами:
1. линейной интерполяции;
2. Лагранжа.
Варианты заданий
| № вар.
| Условие
| f(x)
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| x
|
| 96,2
|
| 104,2
| 108,7
|
|
f (102)
|
| f(x)
| 11,38
| 12,8
| 14,7
| 17,07
| 19,91
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| x
|
|
|
|
|
|
|
f (5)
|
| f(x)
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| x
|
| 2,3
| 2,5
| 3,0
| 3,5
| 3,8
|
|
f (3,75)
|
| f(x)
| 5,848
| 6,127
| 6,3
| 6,694
| 7,047
| 7,243
| 7,368
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| x
|
|
|
|
|
|
f (20)
|
| f(x)
| 68,7
|
|
| 39,1
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| x
|
|
|
|
|
| x при
f (x)=10
|
| f(x)
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| x
|
|
| 2,5
|
|
| x при
f (x)=0
|
| f(x)
| – 6
| – 1
| 5,625
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| x
|
|
|
|
|
| x при
f (x)=20
|
| f(x)
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| x
|
| 1,1
| 1,2
| 1,3
| 1,4
|
|
f (1,13)
|
| f(x)
| 1,1752
| 1,33565
| 1,50946
| 1,69838
| 1,9043
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| x
| 1,5
| 1,6
| 1,7
| 1,8
|
|
f (1,75)
|
| f(x)
| 2,12928
| 2,37587
| 2,64563
| 2,94217
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| x
|
| 1,1
| 1,2
| 1,3
| 1,4
|
|
f (1,23)
|
| f(x)
| 0,6827
| 0,7287
| 0,7699
| 0,8064
| 0,8385
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| x
| 1,5
| 1,6
| 1,6
| 1,7
| 1,8
|
|
f (1,61)
|
| f(x)
| 0,8664
| 0,8904
| 0,9109
| 0,9281
| 0,9426
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| x
| 0,3
| 0,4
| 0,5
| 0,6
| 0,7
|
|
f (0,55)
|
| f(x)
| 0,2913
| 0,3799
| 0,4621
| 0,5380
| 0,6044
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| x
| 0,8
| 0,9
| 1,0
| 1,1
|
|
|
|
f (0,87)
|
| f(x)
| 0,664
| 0,7163
| 0,7616
| 0,8005
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| x
|
| 1,1
| 1,2
| 1,3
| 1,4
|
f (1,25)
|
| f(x)
|
| 0,95135
| 0,91817
| 0,98747
| 0,88726
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| x
|
| 2,2
| 2,4
| 2,6
|
| x при
f (x)=0,1
|
| f(x)
| 0,224
| 0,1104
| 0,0025
| – 0,0968
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| x
| 0,1
| 0,15
| 0,19
| 0,25
|
| x при
f (x)=0,2
|
| f(x)
| 1,1052
| 1,1618
| 1,2092
| 1,284
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| x
| 0,2
| 0,24
| 0,26
| 0,29
|
| f (0,21)
|
| f(x)
| 1,2214
| 1,2712
| 1,2969
| 1,3364
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| x
| 0,1
| 0,13
| 0,17
| 0,2
|
|
f (0,15)
|
| f(x)
| 0,0998
| 0,1296
| 0,1692
| 0,1987
|
|
| |
|
|
|
|
|
|
|
| | | | | | | | | | | | | | | | | | | | |
4.4. Контрольные вопросы
1. В каких случаях прибегают к интерполяции?
2. В чем заключается метод линейной интерполяции?
3. В чем заключается метод Лагранжа?
Лабораторная работа № 5. РЕШЕНИЕ СИСТЕМЫ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Метод Ньютона
Метод Ньютона применяется к решению систем уравнений вида
 ,
,
 – матрица Якоби.
– матрица Якоби.
Тогда последовательные приближения по методу Ньютона вычисляются по формуле:
 ,
,
где 
или
 .
.
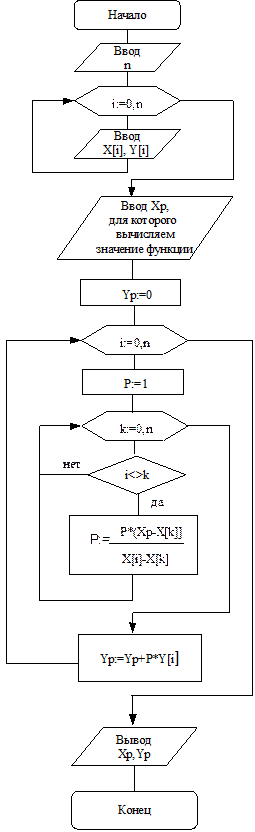
Блок-схема алгоритма решения систем нелинейных уравнений методом Ньютона

Задание
Решить системы нелинейных уравнений методом Ньютона.
Варианты заданий:
| №
варианта
| Система
уравнений
| Точность
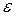
|
|
| 
| 
|
|
| 
| 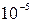
|
|
| 
| 
|
|
| 
| 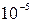
|
|
| 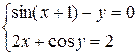
| 
|
|
| 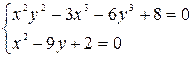
| 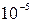
|
|
| 
| 
|
|
| 
| 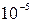
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 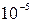
|
|
| 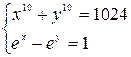
| 
|
|
| 
| 
|
|
| 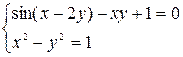
| 
|
|
| 
| 
|
5.3. Контрольные вопросы
1. Как выбрать начальное приближение в методе Ньютона для решения систем нелинейных уравнений?
2. Как определяется матрица Якоби?
3. Какое условие сходимости должно выполняться в методе Ньютона?
Лабораторная работа № 6. РЕШЕНИЕ ЗАДАЧИ АППРОКСИМАЦИИ
Аппроксимация – это процесс определения аналитического вида функции, заданной таблично.
Задача аппроксимации сводится к нахождению свободных параметров функции заданного вида, которые обеспечивают наилучшее приближение функции, заданной таблично.
Наиболее распространенным методом аппроксимации полинома является аппроксимация методом наименьших квадратов.




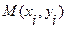
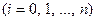 соединяются прямолинейными отрезками и функция
соединяются прямолинейными отрезками и функция 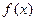 приближается к ломаной с вершинами в данных точках. Поскольку имеется n интервалов
приближается к ломаной с вершинами в данных точках. Поскольку имеется n интервалов 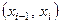 , то для каждого из них в качестве уравнения интерполяционного полинома используется уравнение прямой, проходящей через две точки. В частности для i -го интервала можно записать уравнение прямой, проходящей через точки
, то для каждого из них в качестве уравнения интерполяционного полинома используется уравнение прямой, проходящей через две точки. В частности для i -го интервала можно записать уравнение прямой, проходящей через точки 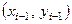 и
и 
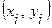 , в виде:
, в виде: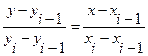
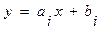 ,
, 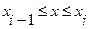 , (4.5)
, (4.5)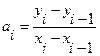 ,
, 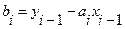 .
.
 ,
, – матрица Якоби.
– матрица Якоби. ,
,
 .
.