При решении задачи синтеза оптимального управления нелинейной динамической системой
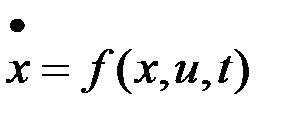 ,
, 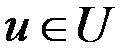 ,
, 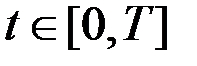 ,
,
обеспечивающего минимум функционалу
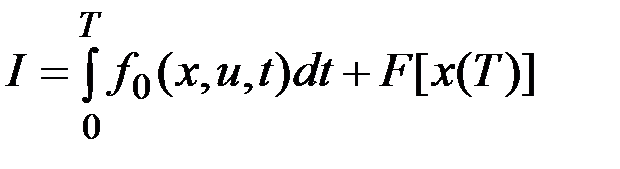 ,
,
часто оказывается возможным указать примерные (достаточно небольшие) области начальных и конечных условий 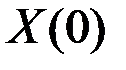 ,
, 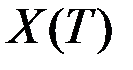 . В этом случае можно предложить следующий метод приближенного решения задачи. Выберем некоторые наиболее ожидаемые или желаемые точки
. В этом случае можно предложить следующий метод приближенного решения задачи. Выберем некоторые наиболее ожидаемые или желаемые точки 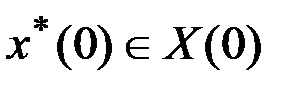 и
и 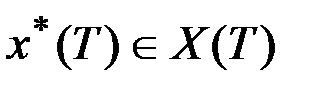 . Обозначим через
. Обозначим через 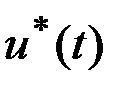 оптимальную программу управления, обеспечивающую перевод из
оптимальную программу управления, обеспечивающую перевод из 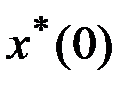 в
в 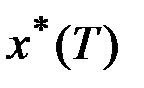 . Траекторию
. Траекторию 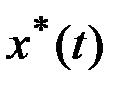 , соответствующую этой программе, назовем невозмущенным, программным движением. Отклонения начального вектора
, соответствующую этой программе, назовем невозмущенным, программным движением. Отклонения начального вектора 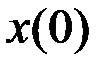 от
от 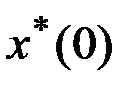 , а также неучтенные факторы приведут к отклонению траектории движения. Для математического описания возмущенного движения воспользуемся методом линеаризации. Представим
, а также неучтенные факторы приведут к отклонению траектории движения. Для математического описания возмущенного движения воспользуемся методом линеаризации. Представим 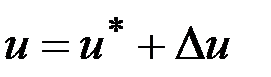 ,
, 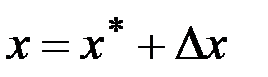 . Тогда получим уравнения движения в отклонениях
. Тогда получим уравнения движения в отклонениях
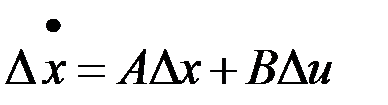 ,
, 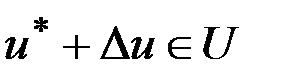 ,
,
где 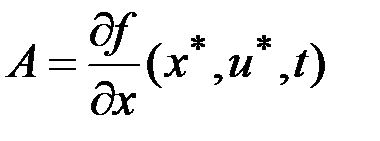 ,
, 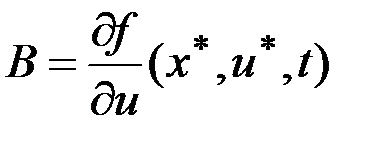 , т.е. матрицы
, т.е. матрицы 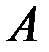 и
и 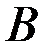 зависят от программного управления
зависят от программного управления 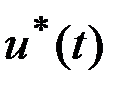 .
.
Желая приблизить действительное (возмущенное) движение к программному (невозмущенному), поставим задачу выбора такого закона управления 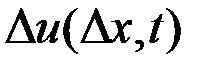 , который позволял бы минимизировать некоторую меру возмущенного движения. В качестве такой меры можно принять, например, квадратичный критерий оптимальности
, который позволял бы минимизировать некоторую меру возмущенного движения. В качестве такой меры можно принять, например, квадратичный критерий оптимальности
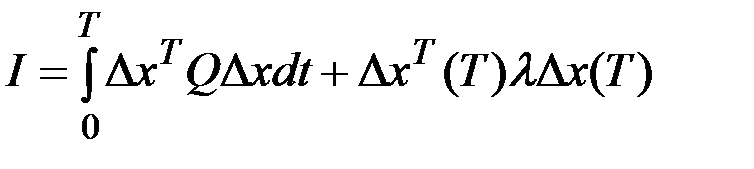 ,
,
где матрицы 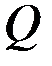 и
и 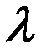 выбираются, исходя из анализа конкретных технических условий.
выбираются, исходя из анализа конкретных технических условий.
При наличии ограничений, накладываемых на вектор управления, задача может оказаться также очень сложной. Можно ее упростить, заменив критерий оптимальности
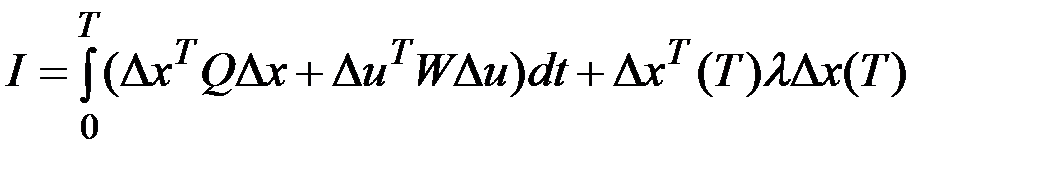 ,
,
в котором 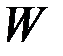 подбирается так, чтобы удовлетворялось ограничение
подбирается так, чтобы удовлетворялось ограничение 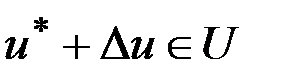 . Решение задачи для линейной системы с таким функционалом было получено ранее и имеет вид
. Решение задачи для линейной системы с таким функционалом было получено ранее и имеет вид 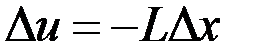 , причем, матрица
, причем, матрица 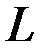 зависит от
зависит от 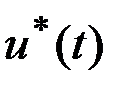 . Таким образом, приближенное решение задачи синтеза для исходной системы может быть представлено в виде
. Таким образом, приближенное решение задачи синтеза для исходной системы может быть представлено в виде
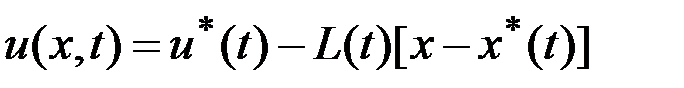 .
.
Оптимальная программа управления 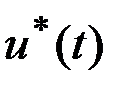 и соответствующая траектория
и соответствующая траектория 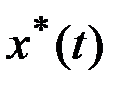 могут быть получены известными методами.
могут быть получены известными методами.
ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ
Теорема Кротова о достаточных условиях
Абсолютного минимума
В предыдущих разделах для решения задач оптимального управления использовались либо необходимые условия оптимальности в форме принципа максимума, либо метод динамического программирования. Рассмотрим достаточные условия оптимальности, знание и проверка которых дает возможность окончательно ответить на вопрос, является ли управление, найденное тем или иным способом, действительно оптимальным.
Пусть на некотором множестве 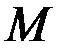 задан функционал
задан функционал 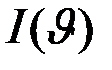 ,
, 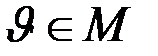 . Введем в рассмотрение множество
. Введем в рассмотрение множество 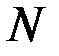 , включающее
, включающее 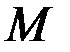 , определив на нем функционал
, определив на нем функционал 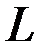 , так, чтобы
, так, чтобы 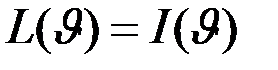 при
при 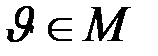 .
.
Лемма. Если элемент 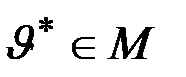 удовлетворяет условию
удовлетворяет условию
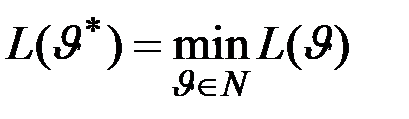 ,
,
то имеет место соотношение
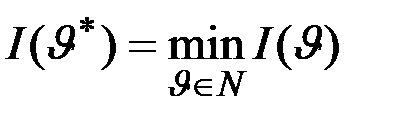 .
.
Доказательство леммы проводится методом от противного. Предположим, что имеется некоторый элемент 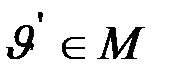 , что
, что 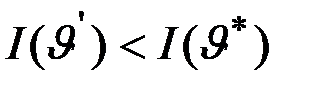 . Но тогда
. Но тогда 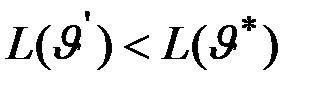 , так как
, так как 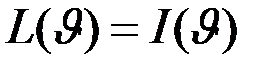 при
при 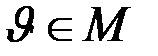 , что противоречит условию.
, что противоречит условию.
Рассмотрим задачу
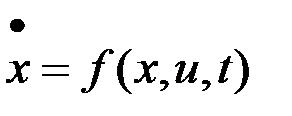 ,
, 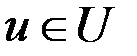 ,
, 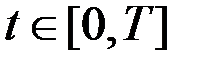 ,
, 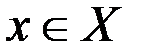 ,
,
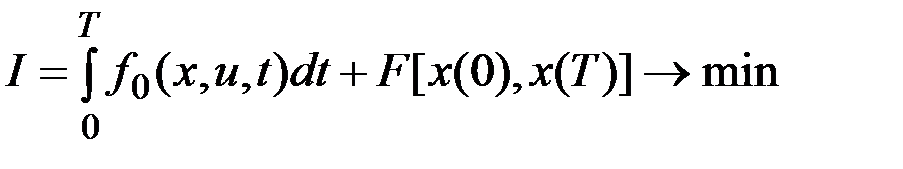 .
.
Обозначим через 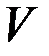 множество пар векторов
множество пар векторов 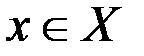 ,
, 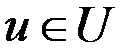 , через
, через 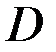 - множество
- множество 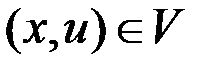 , удовлетворяющих рассматриваемой динамической системе. Задача заключается в отыскании таких
, удовлетворяющих рассматриваемой динамической системе. Задача заключается в отыскании таких 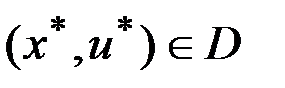 , которые обеспечивают абсолютный минимум функционалу
, которые обеспечивают абсолютный минимум функционалу 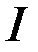 .
.
Введем в рассмотрение функцию 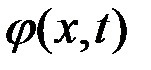 , непрерывную при всех
, непрерывную при всех 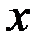 и
и 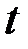 и обладающую непрерывными частными производными
и обладающую непрерывными частными производными 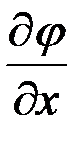 и
и 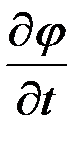 для всех
для всех 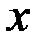 ,
, 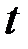 кроме конечного числа точек. Построим функции
кроме конечного числа точек. Построим функции
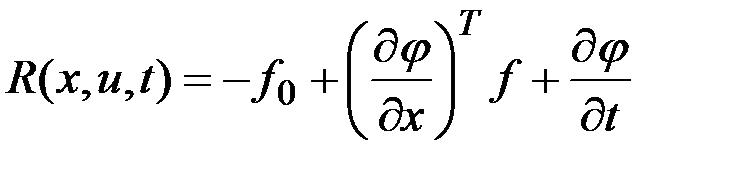 ,
,
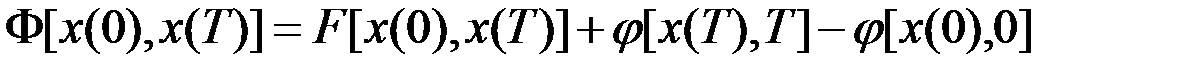 .
.
Теорема. Для того, чтобы функционал 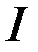 достигал абсолютного минимума на
достигал абсолютного минимума на 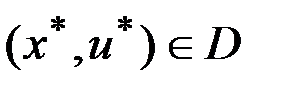 , достаточно существования такой функции
, достаточно существования такой функции 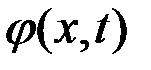 , чтобы:
, чтобы:
1) 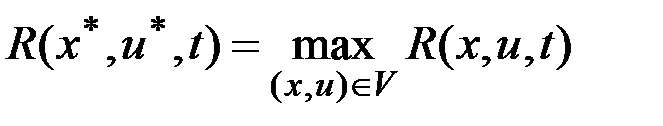 почти всюду на
почти всюду на 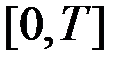 ,
,
2) 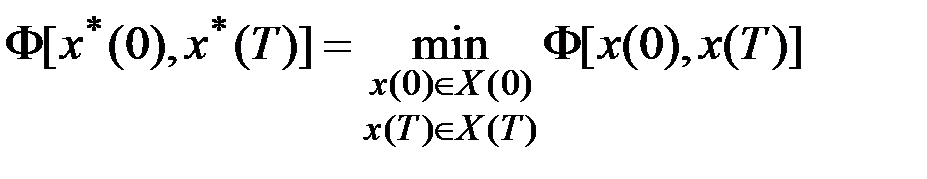 .
.
Для доказательства теоремы используем лемму, ывбрав в качестве 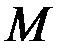 множество
множество 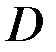 . Под
. Под 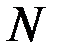 будем понимать множество
будем понимать множество 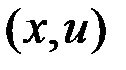 , не связанных исходными уравнениями и допускающих разрывы функции
, не связанных исходными уравнениями и допускающих разрывы функции 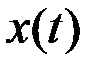 в конечном числе точек. Определим на
в конечном числе точек. Определим на 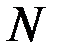 функционал:
функционал:
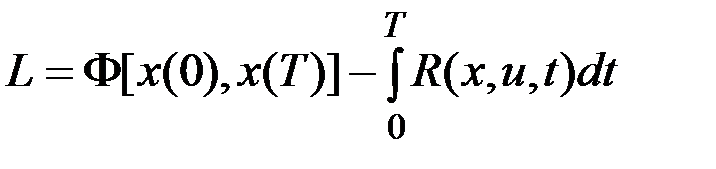 .
.
Можно показать, что на множестве 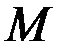 функционалы
функционалы 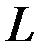 и
и 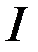 совпадают. Действительно, при
совпадают. Действительно, при 
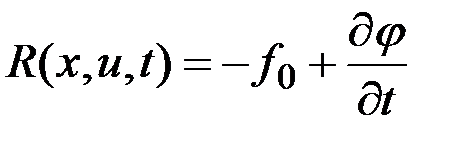 .
.
Подставляя в выражение для 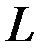 и учитывая, что
и учитывая, что 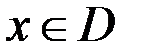 непрерывны, получаем
непрерывны, получаем
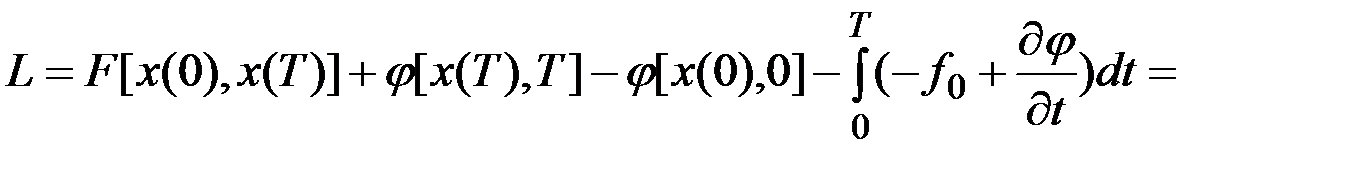
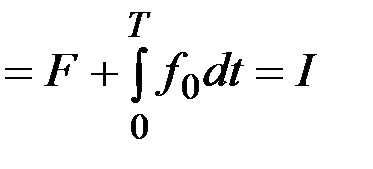 .
.
Так как на множестве 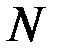 допускаются разрывы функции
допускаются разрывы функции 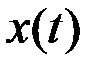 , то слагаемые
, то слагаемые 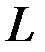 можно рассматривать независимо один от другого. Поэтому
можно рассматривать независимо один от другого. Поэтому
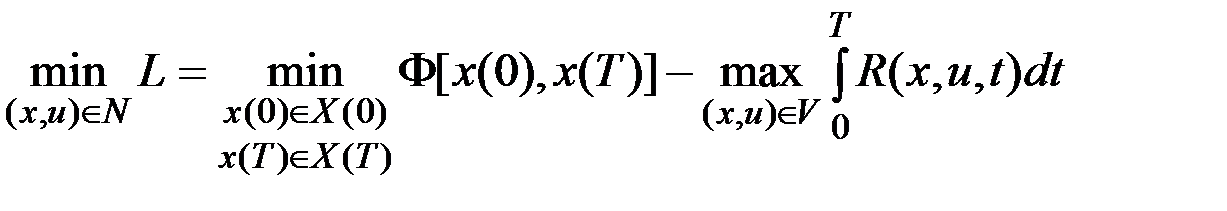 .
.
Если теперь предположить, что 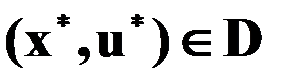 и выполняются условия 1 и 2 теоремы, то согласно последнему выражению
и выполняются условия 1 и 2 теоремы, то согласно последнему выражению 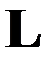 достигает абсолютного минимума на
достигает абсолютного минимума на 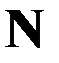 , а в силу леммы функционал
, а в силу леммы функционал 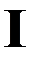 при этом достигает абсолютного минимума на
при этом достигает абсолютного минимума на 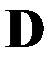 .
.



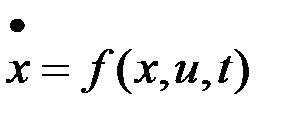 ,
, 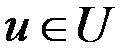 ,
, 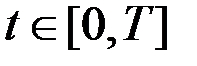 ,
,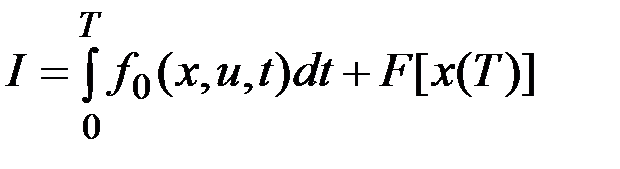 ,
,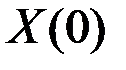 ,
, 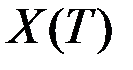 . В этом случае можно предложить следующий метод приближенного решения задачи. Выберем некоторые наиболее ожидаемые или желаемые точки
. В этом случае можно предложить следующий метод приближенного решения задачи. Выберем некоторые наиболее ожидаемые или желаемые точки 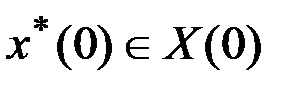 и
и 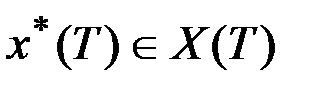 . Обозначим через
. Обозначим через 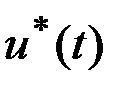 оптимальную программу управления, обеспечивающую перевод из
оптимальную программу управления, обеспечивающую перевод из 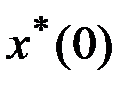 в
в 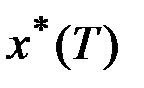 . Траекторию
. Траекторию 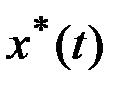 , соответствующую этой программе, назовем невозмущенным, программным движением. Отклонения начального вектора
, соответствующую этой программе, назовем невозмущенным, программным движением. Отклонения начального вектора 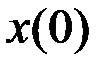 от
от 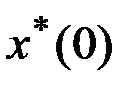 , а также неучтенные факторы приведут к отклонению траектории движения. Для математического описания возмущенного движения воспользуемся методом линеаризации. Представим
, а также неучтенные факторы приведут к отклонению траектории движения. Для математического описания возмущенного движения воспользуемся методом линеаризации. Представим 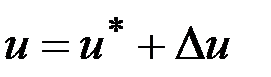 ,
, 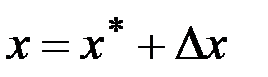 . Тогда получим уравнения движения в отклонениях
. Тогда получим уравнения движения в отклонениях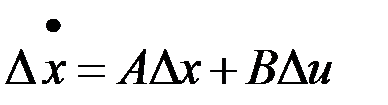 ,
, 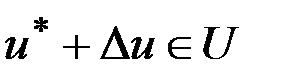 ,
,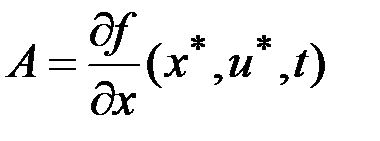 ,
, 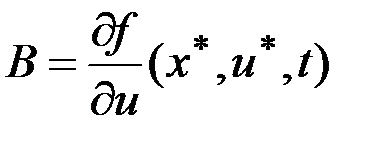 , т.е. матрицы
, т.е. матрицы 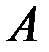 и
и 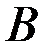 зависят от программного управления
зависят от программного управления 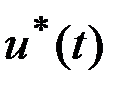 .
.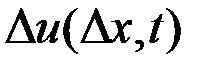 , который позволял бы минимизировать некоторую меру возмущенного движения. В качестве такой меры можно принять, например, квадратичный критерий оптимальности
, который позволял бы минимизировать некоторую меру возмущенного движения. В качестве такой меры можно принять, например, квадратичный критерий оптимальности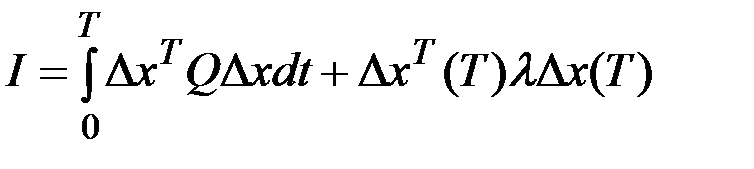 ,
,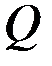 и
и 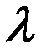 выбираются, исходя из анализа конкретных технических условий.
выбираются, исходя из анализа конкретных технических условий.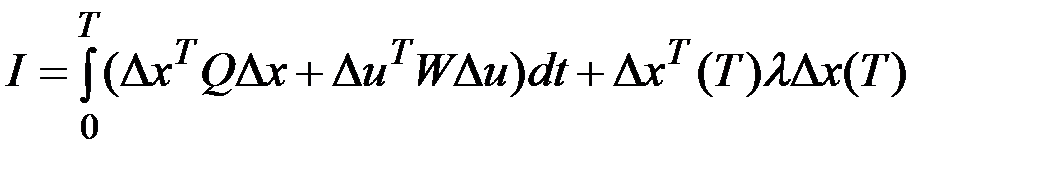 ,
,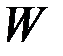 подбирается так, чтобы удовлетворялось ограничение
подбирается так, чтобы удовлетворялось ограничение 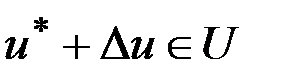 . Решение задачи для линейной системы с таким функционалом было получено ранее и имеет вид
. Решение задачи для линейной системы с таким функционалом было получено ранее и имеет вид 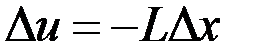 , причем, матрица
, причем, матрица 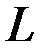 зависит от
зависит от 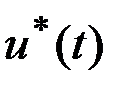 . Таким образом, приближенное решение задачи синтеза для исходной системы может быть представлено в виде
. Таким образом, приближенное решение задачи синтеза для исходной системы может быть представлено в виде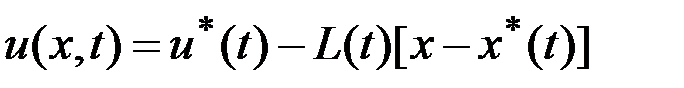 .
.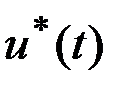 и соответствующая траектория
и соответствующая траектория 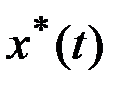 могут быть получены известными методами.
могут быть получены известными методами.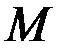 задан функционал
задан функционал 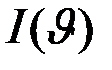 ,
, 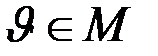 . Введем в рассмотрение множество
. Введем в рассмотрение множество 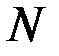 , включающее
, включающее 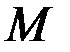 , определив на нем функционал
, определив на нем функционал 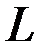 , так, чтобы
, так, чтобы 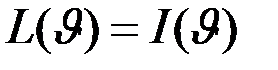 при
при 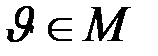 .
.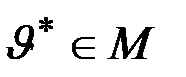 удовлетворяет условию
удовлетворяет условию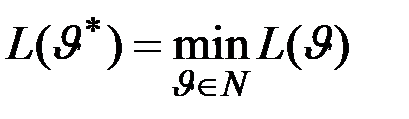 ,
,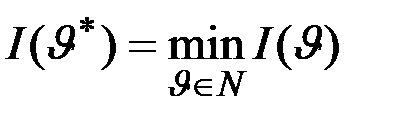 .
.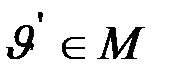 , что
, что 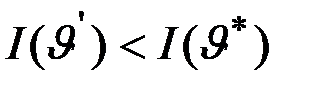 . Но тогда
. Но тогда 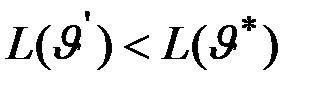 , так как
, так как 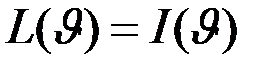 при
при 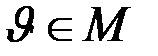 , что противоречит условию.
, что противоречит условию.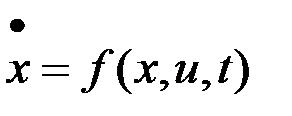 ,
, 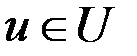 ,
, 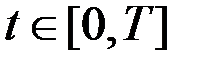 ,
, 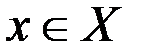 ,
,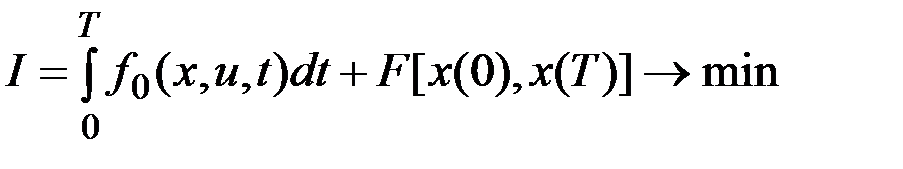 .
.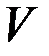 множество пар векторов
множество пар векторов 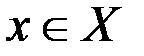 ,
, 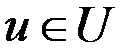 , через
, через 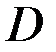 - множество
- множество 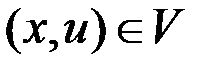 , удовлетворяющих рассматриваемой динамической системе. Задача заключается в отыскании таких
, удовлетворяющих рассматриваемой динамической системе. Задача заключается в отыскании таких 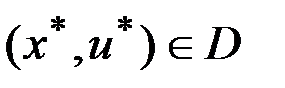 , которые обеспечивают абсолютный минимум функционалу
, которые обеспечивают абсолютный минимум функционалу 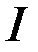 .
.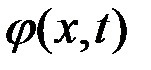 , непрерывную при всех
, непрерывную при всех 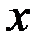 и
и 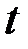 и обладающую непрерывными частными производными
и обладающую непрерывными частными производными 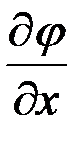 и
и 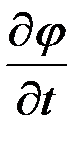 для всех
для всех 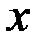 ,
, 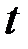 кроме конечного числа точек. Построим функции
кроме конечного числа точек. Построим функции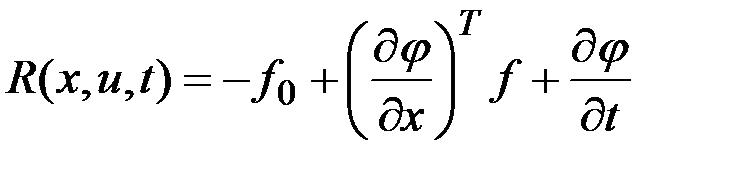 ,
,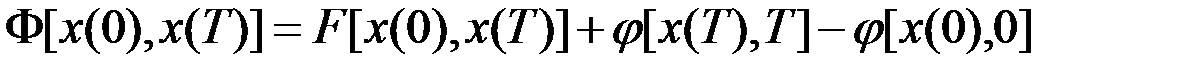 .
.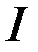 достигал абсолютного минимума на
достигал абсолютного минимума на 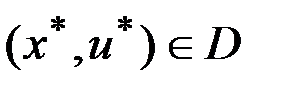 , достаточно существования такой функции
, достаточно существования такой функции 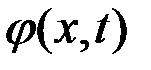 , чтобы:
, чтобы: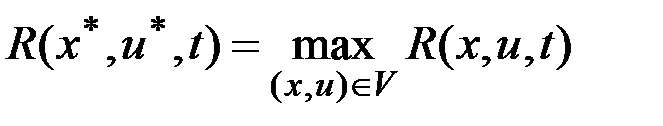 почти всюду на
почти всюду на 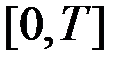 ,
,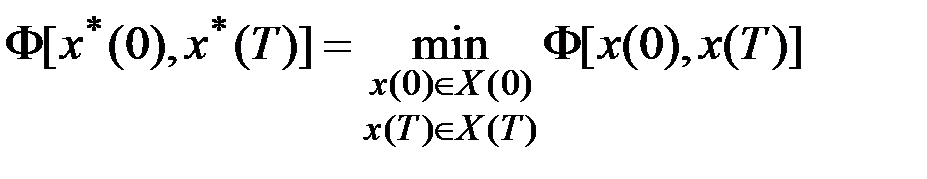 .
.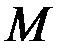 множество
множество 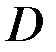 . Под
. Под 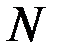 будем понимать множество
будем понимать множество 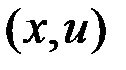 , не связанных исходными уравнениями и допускающих разрывы функции
, не связанных исходными уравнениями и допускающих разрывы функции 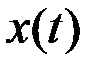 в конечном числе точек. Определим на
в конечном числе точек. Определим на 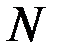 функционал:
функционал: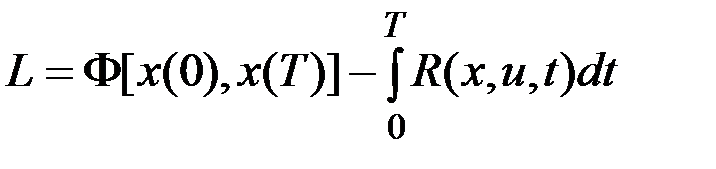 .
.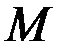 функционалы
функционалы 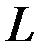 и
и 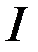 совпадают. Действительно, при
совпадают. Действительно, при 
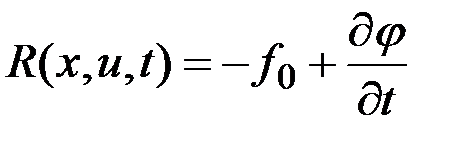 .
.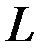 и учитывая, что
и учитывая, что 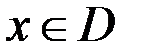 непрерывны, получаем
непрерывны, получаем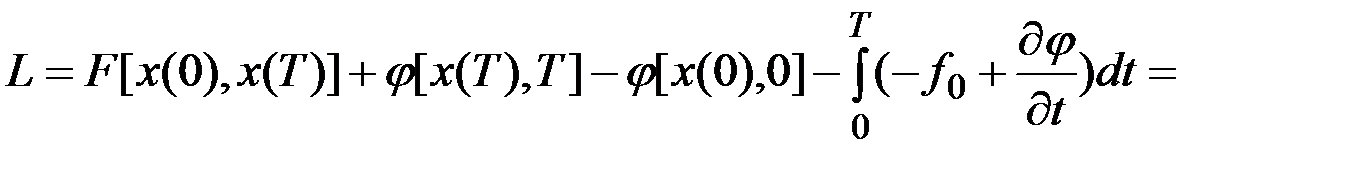
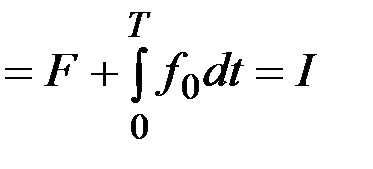 .
.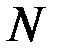 допускаются разрывы функции
допускаются разрывы функции 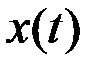 , то слагаемые
, то слагаемые 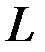 можно рассматривать независимо один от другого. Поэтому
можно рассматривать независимо один от другого. Поэтому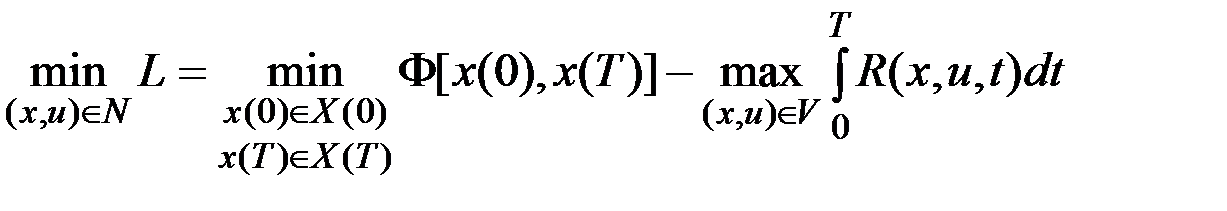 .
.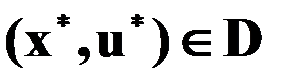 и выполняются условия 1 и 2 теоремы, то согласно последнему выражению
и выполняются условия 1 и 2 теоремы, то согласно последнему выражению 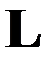 достигает абсолютного минимума на
достигает абсолютного минимума на 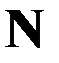 , а в силу леммы функционал
, а в силу леммы функционал 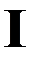 при этом достигает абсолютного минимума на
при этом достигает абсолютного минимума на 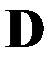 .
.

