С помощью принципа максимума можно вывести необходимые условия существования экстремума в задачах вариационного исчисления. Рассмотрим динамическую управляемую систему с функционалом
 .
.
Пусть  , т.е. управляющие параметры есть скорости изменения фазовых координат. Применим принцип максимума.
, т.е. управляющие параметры есть скорости изменения фазовых координат. Применим принцип максимума.
Составим гамильтониан:  . Используем необходимое условие максимума гамильтониана:
. Используем необходимое условие максимума гамильтониана:
 ,
,  .
.
Продифференцируем выражение для  по времени:
по времени: 
Согласно канонического уравнения для сопряженных переменных
 .
.
Сопоставляя два последних выражения, получим уравнение Эйлера
 .
.
Условие второго порядка для существования максимума функции Гамильтона определяется как условие отрицательной определенности матрицы вторых частных производных гамильтониана, т.е. матрицы 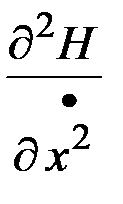 . Из этого условия следует условие положительной определенности матрицы
. Из этого условия следует условие положительной определенности матрицы  , или
, или 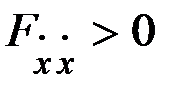 , т.е. условие Лежандра.
, т.е. условие Лежандра.
Согласно принципу максимума, если  является оптимальным управлением, то при любом другом управлении
является оптимальным управлением, то при любом другом управлении 
 .
.
Учитывая выражение для гамильтониана, получаем неравенство:
 , или
, или
 ,
,
которое есть условие Вейерштрасса.
Таким образом, с помощью принципа максимума получены необходимые условия экстремума в задачах классического вариационного исчисления.
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Принцип оптимальности Беллмана.
Уравнение Беллмана
В основе метода динамического программирования лежит принцип оптимальности, сформулированный Р.Беллманом: оптимальный процесс обладает тем свойством, что каким бы ни было начальное управление последующее управление должно быть оптимальным по отношению к состоянию, происходящему от начального управления.
Предположим, что  - оптимальная траектория, приводящая систему из начального состояния
- оптимальная траектория, приводящая систему из начального состояния  в конечное
в конечное  , промежуточное состояние
, промежуточное состояние  соответствует моменту времени
соответствует моменту времени  (рис.4.1). Согласно принципу оптимальности Беллмана участок траектории
(рис.4.1). Согласно принципу оптимальности Беллмана участок траектории  представляет собой оптимальную траекторию по отношению к начальному состоянию
представляет собой оптимальную траекторию по отношению к начальному состоянию  , т.е. оптимальное управление на участке
, т.е. оптимальное управление на участке  не зависит от того, каким образом система приведена в состояние
не зависит от того, каким образом система приведена в состояние  .
.
Рис.4.1. Оптимальная траектория
Другими словами, каждый участок оптимальной траектории является оптимальной траекторией относительно своей начальной точки, оптимальное управление не зависит от предыстории движения системы и для будущих моментов времени определяется только состоянием в данный момент. Таким образом, всю траекторию движения системы можно разбить на части, двигаясь от ее конца к началу, и оптимизировать движение по частям.
Рассмотрим задачу оптимального управления динамической системой:
 ,
,  ,
,  ,
,  ,
, 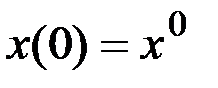 ,
,  ,
,
 .
.
Требуется синтезировать закон оптимального управления  .
.
Пусть поставленная задача решена. Введем обозначение:  - минимальное значение функционала для участка траектории
- минимальное значение функционала для участка траектории  , тогда
, тогда  - есть минимальное значение функционала
- есть минимальное значение функционала  для измененного относительно
для измененного относительно 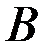 состояния и времени. Очевидно, что
состояния и времени. Очевидно, что  . Тогда в общем случае независимых изменений состояния и времени получим в соответствии с принципом оптимальности Беллмана
. Тогда в общем случае независимых изменений состояния и времени получим в соответствии с принципом оптимальности Беллмана
 .
.
Введем допущения о том, что функция  непрерывна и непрерывно дифференцируема (во многих задачах эти условия не выполняются). Разложим
непрерывна и непрерывно дифференцируема (во многих задачах эти условия не выполняются). Разложим 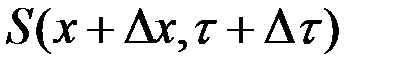 в ряд Тейлора, отбросив малые величины, получим
в ряд Тейлора, отбросив малые величины, получим
 .
.
Подставив в предыдущее выражение, получим
 .
.
Разделив на  , при
, при  получим
получим
 .
.
Полученное нелинейное дифференциальное уравнение в частных производных относительно функции  называется уравнением Беллмана. При решении конкретных задач аналитическое решение можно получить лишь в некоторых частных случаях. В общем случае уравнение Беллмана решается численно.
называется уравнением Беллмана. При решении конкретных задач аналитическое решение можно получить лишь в некоторых частных случаях. В общем случае уравнение Беллмана решается численно.
Функция  есть функция текущего состояния системы, ее принято называть функцией будущих потерь или функцией Беллмана. Она является мерой стоимости перехода из точки с координатами
есть функция текущего состояния системы, ее принято называть функцией будущих потерь или функцией Беллмана. Она является мерой стоимости перехода из точки с координатами 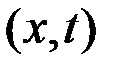 в точку с координатами
в точку с координатами  . В задаче Больца функция будущих потерь в конечный момент времени равна терминальному члену, т.е.
. В задаче Больца функция будущих потерь в конечный момент времени равна терминальному члену, т.е.  , в задаче Лагранжа
, в задаче Лагранжа  , следовательно,
, следовательно,  . Эти выражения задают граничные условия для уравнения Беллмана.
. Эти выражения задают граничные условия для уравнения Беллмана.



 .
. , т.е. управляющие параметры есть скорости изменения фазовых координат. Применим принцип максимума.
, т.е. управляющие параметры есть скорости изменения фазовых координат. Применим принцип максимума. . Используем необходимое условие максимума гамильтониана:
. Используем необходимое условие максимума гамильтониана: ,
,  .
. по времени:
по времени: 
 .
. .
.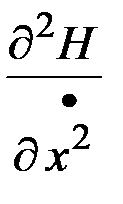 . Из этого условия следует условие положительной определенности матрицы
. Из этого условия следует условие положительной определенности матрицы  , или
, или 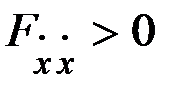 , т.е. условие Лежандра.
, т.е. условие Лежандра. является оптимальным управлением, то при любом другом управлении
является оптимальным управлением, то при любом другом управлении 
 .
. , или
, или ,
, - оптимальная траектория, приводящая систему из начального состояния
- оптимальная траектория, приводящая систему из начального состояния  в конечное
в конечное  , промежуточное состояние
, промежуточное состояние  соответствует моменту времени
соответствует моменту времени  (рис.4.1). Согласно принципу оптимальности Беллмана участок траектории
(рис.4.1). Согласно принципу оптимальности Беллмана участок траектории  представляет собой оптимальную траекторию по отношению к начальному состоянию
представляет собой оптимальную траекторию по отношению к начальному состоянию  , т.е. оптимальное управление на участке
, т.е. оптимальное управление на участке  не зависит от того, каким образом система приведена в состояние
не зависит от того, каким образом система приведена в состояние  .
.

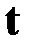
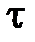

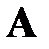

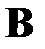



 ,
,  ,
,  ,
,  ,
, 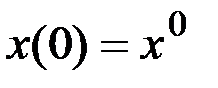 ,
,  ,
, .
. .
. - минимальное значение функционала для участка траектории
- минимальное значение функционала для участка траектории  , тогда
, тогда  - есть минимальное значение функционала
- есть минимальное значение функционала  для измененного относительно
для измененного относительно 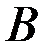 состояния и времени. Очевидно, что
состояния и времени. Очевидно, что  . Тогда в общем случае независимых изменений состояния и времени получим в соответствии с принципом оптимальности Беллмана
. Тогда в общем случае независимых изменений состояния и времени получим в соответствии с принципом оптимальности Беллмана .
. непрерывна и непрерывно дифференцируема (во многих задачах эти условия не выполняются). Разложим
непрерывна и непрерывно дифференцируема (во многих задачах эти условия не выполняются). Разложим 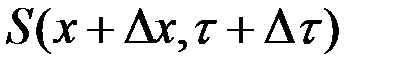 в ряд Тейлора, отбросив малые величины, получим
в ряд Тейлора, отбросив малые величины, получим .
. .
. , при
, при  получим
получим .
. называется уравнением Беллмана. При решении конкретных задач аналитическое решение можно получить лишь в некоторых частных случаях. В общем случае уравнение Беллмана решается численно.
называется уравнением Беллмана. При решении конкретных задач аналитическое решение можно получить лишь в некоторых частных случаях. В общем случае уравнение Беллмана решается численно. есть функция текущего состояния системы, ее принято называть функцией будущих потерь или функцией Беллмана. Она является мерой стоимости перехода из точки с координатами
есть функция текущего состояния системы, ее принято называть функцией будущих потерь или функцией Беллмана. Она является мерой стоимости перехода из точки с координатами 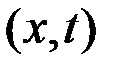 в точку с координатами
в точку с координатами  . В задаче Больца функция будущих потерь в конечный момент времени равна терминальному члену, т.е.
. В задаче Больца функция будущих потерь в конечный момент времени равна терминальному члену, т.е.  , в задаче Лагранжа
, в задаче Лагранжа  , следовательно,
, следовательно,  . Эти выражения задают граничные условия для уравнения Беллмана.
. Эти выражения задают граничные условия для уравнения Беллмана.


