

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Интересное:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Рассмотрим некоторый функционал  и его приращение
и его приращение  , где
, где  - вариация
- вариация 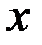 .
.
Определение. Вариацией функции  , принадлежащей определенному классу функций, называется разность между двумя функциями при одинаковом значении аргумента
, принадлежащей определенному классу функций, называется разность между двумя функциями при одинаковом значении аргумента  :
:  .
.
Определение. Если  можно представить в виде
можно представить в виде
 , (2.4)
, (2.4)
где  при
при 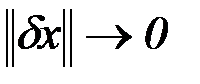 , то линейная по отношению к
, то линейная по отношению к 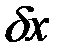 часть приращения функционала, т.е.
часть приращения функционала, т.е.  , называется вариацией функционала и обозначается
, называется вариацией функционала и обозначается 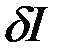 .
.
Функционал достигает экстремума при  , если величина приращения функционала
, если величина приращения функционала  сохраняет свой знак в некоторой окрестности
сохраняет свой знак в некоторой окрестности  . Различают сильный и слабый экстремумы.
. Различают сильный и слабый экстремумы.
Если существует величина  , что
, что  сохраняет знак для всех
сохраняет знак для всех  , входящих в пространство (класс)
, входящих в пространство (класс)  , у которых норма
, у которых норма  , то говорят, что при
, то говорят, что при  достигается слабый экстремум функционала. Аналогично, экстремум называется сильным, если
достигается слабый экстремум функционала. Аналогично, экстремум называется сильным, если  сохраняет знак для всех
сохраняет знак для всех  и удовлетворяет условию
и удовлетворяет условию  . Всякий сильный экстремум будет одновременно и слабым, а слабый сильным быть не может, так как достигается на более узком множестве функций.
. Всякий сильный экстремум будет одновременно и слабым, а слабый сильным быть не может, так как достигается на более узком множестве функций.
Теорема. Для того, чтобы функционал  достигал экстремума при
достигал экстремума при  , необходимо, чтобы при
, необходимо, чтобы при 
 .
.
Доказательство
Пусть функционал имеет минимум при  , тогда
, тогда
 .
.
С другой стороны 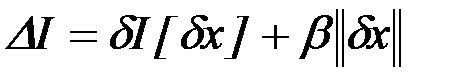 .
.
При достаточно малом  знак
знак  определяется знаком
определяется знаком  , а в силу линейности
, а в силу линейности  имеем:
имеем:  . Следовательно,
. Следовательно,  может быть и меньше и больше 0 при сколь угодно малом
может быть и меньше и больше 0 при сколь угодно малом 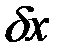 разного знака, т.е. экстремум невозможен. Противоречие устраняется, если
разного знака, т.е. экстремум невозможен. Противоречие устраняется, если 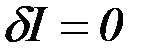 . Аналогично доказывается необходимое условие максимума функционала.
. Аналогично доказывается необходимое условие максимума функционала.
2.3. Простейшая задача вариационного исчисления
(задача с закрепленными концами). Основная лемма
Вариационного исчисления. Уравнение Эйлера
Простейшей задачей вариационного исчисления называется задача об экстремуме функционала вида (2.1) с граничными условиями 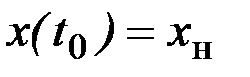 ,
,  .
.
|
|
Лемма. Если для каждой непрерывной функции 
 ,
,
где функция 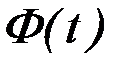 непрерывна на отрезке
непрерывна на отрезке  , то
, то  на том же отрезке.
на том же отрезке.
Доказательство
Предположив, что в точке  , лежащей на отрезке
, лежащей на отрезке  ,
,  , придем к противоречию. Действительно, из непрерывности функции
, придем к противоречию. Действительно, из непрерывности функции  следует, что если
следует, что если 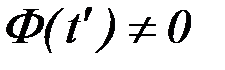 , то
, то 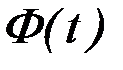 сохраняет знак в некоторой окрестности
сохраняет знак в некоторой окрестности  точки
точки  ; выбрав функцию
; выбрав функцию 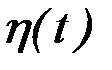 также сохраняющую знак в этой окрестности и равную нулю вне этой окрестности, получим
также сохраняющую знак в этой окрестности и равную нулю вне этой окрестности, получим
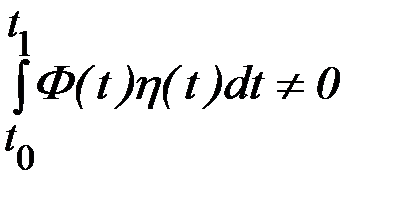 ,
,
так как произведение  сохраняет знак на интервале
сохраняет знак на интервале  и обращается в нуль вне этого отрезка. Итак, мы пришли к противоречию, следовательно,
и обращается в нуль вне этого отрезка. Итак, мы пришли к противоречию, следовательно,  .
.
Теорема. Для того, чтобы функционал
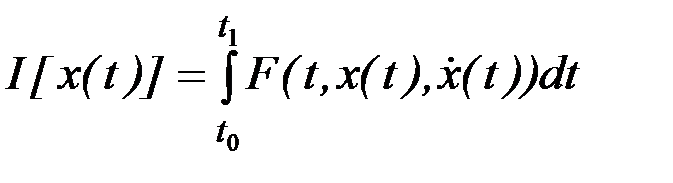 ,
,
определенный на множестве непрерывных функций  , имеющих непрерывную первую производную и удовлетворяющих граничным условиям
, имеющих непрерывную первую производную и удовлетворяющих граничным условиям  ,
,  , достигал на
, достигал на  экстремума, необходимо, чтобы функция
экстремума, необходимо, чтобы функция  удовлетворяла уравнению Эйлера
удовлетворяла уравнению Эйлера
 , (2.5)
, (2.5)
или в развернутом виде
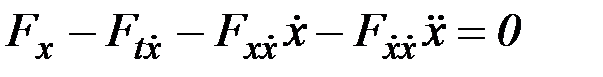 . (2.6)
. (2.6)
Доказательство
Получим формулу для первой вариации функционала. Применяя операцию варьирования подынтегрального выражения при условии, что  , получим
, получим
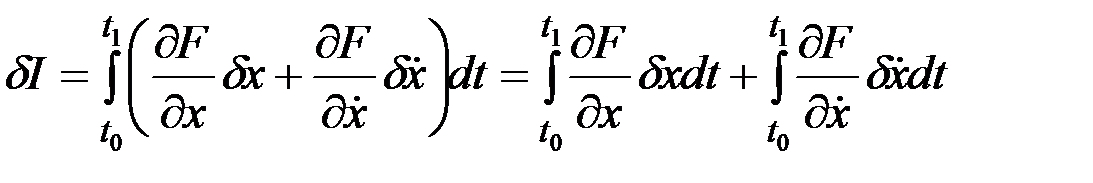 . (2.7)
. (2.7)
Проинтегрируем второе слагаемое по частям и, принимая во внимание, что 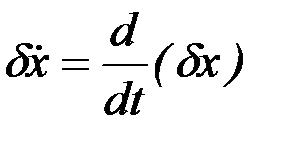 , получим
, получим
 . (2.8)
. (2.8)
Но поскольку концы экстремали закреплены, то  ,
,  , и получаем необходимое условие экстремума в виде
, и получаем необходимое условие экстремума в виде
 . (2.9)
. (2.9)
В силу основной леммы вариационного исчисления, поскольку  , получаем результат (2.5).
, получаем результат (2.5).
Интегральные кривые уравнения Эйлера  называются экстремалями, только на них достигается экстремум рассматриваемого функционала. Чтобы установить, реализуется ли на них в действительности экстремум, и притом максимум или минимум, надо воспользоваться достаточными условиями экстремума.
называются экстремалями, только на них достигается экстремум рассматриваемого функционала. Чтобы установить, реализуется ли на них в действительности экстремум, и притом максимум или минимум, надо воспользоваться достаточными условиями экстремума.
Краевая задача для уравнения (2.6) с граничными условиями 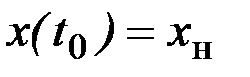 ,
,  не всегда имеет решение, а если решение существует, то оно может быть не единственным.
не всегда имеет решение, а если решение существует, то оно может быть не единственным.
Получим необходимые условия экстремума функционала  , зависящего от
, зависящего от  независимых функций
независимых функций  :
:

при заданных граничных условиях всех функций
 ,
,  ,...,
,...,  ,
,
|
|
 ,
,  ,...,
,...,  .
.
Если варьировать одну из функций 
 , оставляя остальные неизменными, то рассматриваемый функционал превращается в функционал, зависящий лишь от одной функции, которая, следовательно, должна удовлетворять уравнению Эйлера
, оставляя остальные неизменными, то рассматриваемый функционал превращается в функционал, зависящий лишь от одной функции, которая, следовательно, должна удовлетворять уравнению Эйлера
 .
.
Так как это рассуждение применимо к любой функции 
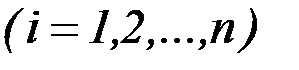 , то мы получим систему дифференциальных уравнений второго порядка
, то мы получим систему дифференциальных уравнений второго порядка

 , (2.10)
, (2.10)
определяющих  -параметрическое семейство интегральных кривых (экстремалей).
-параметрическое семейство интегральных кривых (экстремалей).
Поле экстремалей
Если на плоскости  через каждую точку некоторой области
через каждую точку некоторой области  проходит одна и только одна кривая семейства
проходит одна и только одна кривая семейства  , говорят, что это семейство кривых в области
, говорят, что это семейство кривых в области 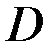 образует собственное поле. Угловой коэффициент касательной
образует собственное поле. Угловой коэффициент касательной 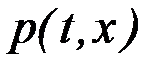 к кривой семейства
к кривой семейства  , проходящей через точку
, проходящей через точку  , называется наклоном поляв точке
, называется наклоном поляв точке  :
:  .
.
Поле называется центральным, если кривые покрывают всю область 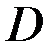 и нигде не пересекаются кроме одной точки (центра пучка кривых), принадлежащей области
и нигде не пересекаются кроме одной точки (центра пучка кривых), принадлежащей области 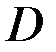 .
.
Если собственное или центральное поле образовано семейством экстремалей некоторой вариационной задачи, то оно называется полем экстремалей.
Говорят, что экстремаль 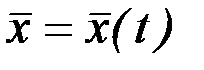 включена в поле экстремалей, если найдено семейство экстремалей
включена в поле экстремалей, если найдено семейство экстремалей  , образующее поле, содержащее при некотором значении
, образующее поле, содержащее при некотором значении 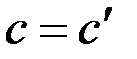 экстремаль
экстремаль 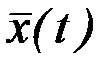 , причем последняя не лежит на границе области
, причем последняя не лежит на границе области  .
.
Известно, что две бесконечно близкие кривые семейства 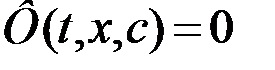 пересекаются в точках
пересекаются в точках  -дискриминантной кривой, определяемой уравнениями
-дискриминантной кривой, определяемой уравнениями
 ,
, 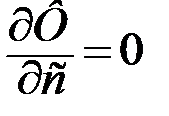 .
.
Если дуга  экстремали
экстремали 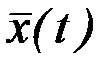 не имеет отличных от точки
не имеет отличных от точки  общих точек с
общих точек с  -дискриминантной кривой пучка экстремалей, включающего данную экстремаль, то достаточно близкие к дуге
-дискриминантной кривой пучка экстремалей, включающего данную экстремаль, то достаточно близкие к дуге  экстремали пучка не пересекаются, т.е. образуют в окрестности дуги
экстремали пучка не пересекаются, т.е. образуют в окрестности дуги  центральное поле, включающее эту дугу.
центральное поле, включающее эту дугу.
Если дуга  экстремали
экстремали 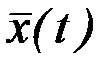 имеет отличную от точки
имеет отличную от точки  общую точку
общую точку  с
с  -дискриминантной кривой пучка экстремалей, то близкие кривые пучка могут пересекаться между собой вблизи точки
-дискриминантной кривой пучка экстремалей, то близкие кривые пучка могут пересекаться между собой вблизи точки  и, вообще говоря, поля не образуют. Точка
и, вообще говоря, поля не образуют. Точка  называется точкой, сопряженной с точкой
называется точкой, сопряженной с точкой  и является точкой пересечения двух бесконечно близких кривых семейства
и является точкой пересечения двух бесконечно близких кривых семейства  .
.
Условие Якоби. Для построения центрального поля экстремалей с центром в точке  , содержащего дугу
, содержащего дугу  экстремали, достаточно, чтобы точка
экстремали, достаточно, чтобы точка  , сопряженная с точкой
, сопряженная с точкой  , не лежала на дуге
, не лежала на дуге  .
.
|
|
|

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!