

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Любое предположение о случайной величине X, законе её распределения, параметрах, числовых характеристиках и т. п. назовём статистической гипотезой. Решение принять или отвергнуть гипотезу H будем принимать по выборке. Всё выборочное пространство W распадается, таким образом, на два множества W H и  , W=W H +
, W=W H +  . При попадании выборочной точки в W H гипотеза H отвергается, при попадании в
. При попадании выборочной точки в W H гипотеза H отвергается, при попадании в  гипотеза H принимается. Множество W H называется критической областью для данной гипотезы H. Чтобы определить процедуру проверки гипотезы H, достаточно задать критическую область W H. При такой договорённости мы можем совершить ошибки двух родов: ошибка первого рода состоит в отвержении верной гипотезы, ошибка второго рода состоит в принятии неверной гипотезы. Конкретные примеры показывают, что часто эти ошибки имеют весьма различный характер и значительно отличаются по своим конкретным последствиям. Иногда одна из ошибок бывает заметно более опасной, чем другая, и гипотезу H обычно формулируют так, чтобы ошибка первого рода была более опасной, и мы будем стремиться контролировать прежде всего её. Чтобы переставить ошибки местами, достаточно проверять вместо H гипотезу
гипотеза H принимается. Множество W H называется критической областью для данной гипотезы H. Чтобы определить процедуру проверки гипотезы H, достаточно задать критическую область W H. При такой договорённости мы можем совершить ошибки двух родов: ошибка первого рода состоит в отвержении верной гипотезы, ошибка второго рода состоит в принятии неверной гипотезы. Конкретные примеры показывают, что часто эти ошибки имеют весьма различный характер и значительно отличаются по своим конкретным последствиям. Иногда одна из ошибок бывает заметно более опасной, чем другая, и гипотезу H обычно формулируют так, чтобы ошибка первого рода была более опасной, и мы будем стремиться контролировать прежде всего её. Чтобы переставить ошибки местами, достаточно проверять вместо H гипотезу 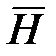 .
.
Сужая критическую область, мы уменьшаем вероятность ошибки первого рода, но при этом, как правило, возрастает вероятность ошибки второго рода, и наоборот. Чтобы сделать вероятность ошибки первого рода равной нулю, достаточно взять W H =Æ, но при этом мы будем принимать и все неверные гипотезы; если взять W H =W, то вероятность ошибки второго рода будет равна нулю, но при этом мы обязательно будем отвергать и все верные гипотезы. Уменьшая одну ошибку, мы расплачиваемся увеличением другой.
|
|
Во всей описанной схеме (её авторами являются Ю. Нейман и Д. Пирсон) ничего пока не говорилось о том, как гарантировать принятие истинной и отвержение ложной гипотезы. Основываясь на случайной выборке, мы не можем с абсолютной надёжностью (например, почти наверное) давать такую гарантию (исключение составляют лишь вырожденные случаи), а следовательно, не берёмся доказывать истинность или ложность гипотезы. Мы лишь проверяем, кажутся ли экспериментальные данные согласующимися с гипотезой, или, видимо, ей противоречат. Удовольствуемся следующим: будет хорошо, если отвергать верную гипотезу (т.е. совершать ошибку первого рода) и принимать ложную гипотезу (т.е. совершать ошибку второго рода) мы будем достаточно редко, – с заданной, достаточно малой или контролируемой удовлетворительной вероятностью.
Обозначим a и b вероятности ошибок первого и второго рода:
a= P ({(x 1, x 2, ¼, xn)ÎW H | H }, b= P ({(x 1, x 2, ¼, xn)Î  |
| 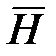 }.
}.
Отсюда ясно, что мы можем контролировать a, если знаем, при условии справедливости гипотезы H, закон распределения случайной величины X, и можем контролировать b, если знаем этот закон при условии справедливости гипотезы 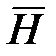 . Гипотезу, при которой закон распределения случайной величины X однозначно определяется, называют нулевой гипотезой. И здесь возникает существенная трудность: если гипотеза H нулевая, то обычно
. Гипотезу, при которой закон распределения случайной величины X однозначно определяется, называют нулевой гипотезой. И здесь возникает существенная трудность: если гипотеза H нулевая, то обычно 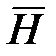 уже ненулевая и если H не верна, то мы, как правило, не знаем, что имеет место в действительности, а поэтому и не можем контролировать b. Выход может состоять в том, что мы вычисляем b для наиболее интересных, или наиболее опасных, или наиболее вероятных альтернатив.
уже ненулевая и если H не верна, то мы, как правило, не знаем, что имеет место в действительности, а поэтому и не можем контролировать b. Выход может состоять в том, что мы вычисляем b для наиболее интересных, или наиболее опасных, или наиболее вероятных альтернатив.
Чаще всего критическая область строится с помощью некоторой функции от выборки K (x 1, x 2, ¼, xn), называемой критерием. Ниже в наших примерах критическая зона определяется по критерию из неравенства K (x 1, x 2, ¼, xn)> C, где C – пороговое значение критерия, и тогда вероятности ошибок выглядят так:
a= P (K (x 1, x 2, ¼, xn)> C | H }, b= P (K (x 1, x 2, ¼, xn)£ C | 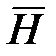 }.
}.
|
|
Из этих формул видно, что мы можем контролировать a и b, если будем знать закон распределения критерия K как случайной величины, хотя бы приближённо при условии справедливости гипотезы H и при условии справедливости гипотезы 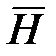 .
.
Для данной гипотезы H обычно удаётся подобрать такой критерий K, что закон распределения его при истинности гипотезы H известен, и a можно контролировать. Однако, при истинности 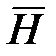 мы, вообще говоря, не можем оценить b, но утешением оказывается то обстоятельство, что для хорошо подобранных критериев при n ®¥ вероятность b®0, и хотя мы не можем её вычислить, всё-таки остается уверенность, что при достаточно большом объёме выборки ошибка второго рода будет как угодно мала. Известная опасность кроется в том, что мы, как правило, не можем сказать, достаточно ли большим является доступный нам объём выборки.
мы, вообще говоря, не можем оценить b, но утешением оказывается то обстоятельство, что для хорошо подобранных критериев при n ®¥ вероятность b®0, и хотя мы не можем её вычислить, всё-таки остается уверенность, что при достаточно большом объёме выборки ошибка второго рода будет как угодно мала. Известная опасность кроется в том, что мы, как правило, не можем сказать, достаточно ли большим является доступный нам объём выборки.
Максимально допустимую величину вероятности ошибки первого рода a называют уровнем значимости критерия; задав a, находят порог C из условия:
P (K > C | H }=a.
Обычные значения уровня значимости для практики: a=0,01; 0,05; 0,1. (В дискретном случае, правда, в качестве значений a могут быть не любые числа, и это надо учитывать, иначе только что написанное уравнение окажется неразрешимым). Уравнение же решается по таблицам точного или приближённого закона распределения критерия K.
Например, построив критическую область для уровня значимости a=0,05, мы должны считаться с тем, что в сотне применений критерия мы в среднем пять раз отвергнем гипотезу, которая на самом деле верна. Если фактические последствия этих ошибок нас не пугают, то можем пользоваться данной критической областью. Если же они представляются неприемлемыми, то можем уменьшить a, но при этом увеличится b, и мы должны взвесить: приемлемы ли для нас последствия ошибок второго рода. Если нет, то остаётся либо отказаться от изучаемого критерия, либо увеличить число наблюдений: для разумно выбранного критерия при этом a и b уменьшаются.
Критерий должен обладать свойством реагировать на правильность или ошибочность гипотезы: он должен иметь тенденцию быть малым, если гипотеза верна, и быть большим, если она ошибочна.
Ясно, что если критерий ведёт себя наоборот, т. е. принимает малые значения, если гипотеза ошибочна, и большая, если она верна, то это тоже нас устроит; нужно лишь составлять критическую область из малых значений критерия.
|
|
Рассмотрим три важнейших критерия математической статистики: Колмогорова, Пирсона, Стьюдента.
Критерий Колмогорова
Пусть X – непрерывная случайная величина. Проверяется гипотеза H: некоторая функция F (x) является ни чем иным, как функцией распределения случайной величины X.
А. Н. Колмогоров доказал следующую теорему:
если F (x) – истинная функция распределения, то при " С >0:
 P {
P { 
 | Fn (x)- F (x)|> C }=2
| Fn (x)- F (x)|> C }=2  (-1) k +1 e -2 k 2 C 2.
(-1) k +1 e -2 k 2 C 2.
Стоящая справа сумма – одна из семейства тета-функций – табулирована и не представляет трудностей при работе.
Считаем, что n достаточно велико, чтобы было справедливо приближённое равенство:
P { 
 | Fn (x)- F (x)|> C }»2
| Fn (x)- F (x)|> C }»2  (-1) k +1 e -2 k 2 C 2.
(-1) k +1 e -2 k 2 C 2.
Теорема Колмогорова подсказывает нам выбор критерия для проверки гипотезы H:
K (x 1, x 2, ¼, xn)= 
 | Fn (x)- F (x)|.
| Fn (x)- F (x)|.
Если H верна, то эмпирическая функция Fn (x) близка к истинной функции распределения F (x): Fn (x)» F (x), и критерий имеет тенденцию быть малым. Если H не верна, то истинная функция распределения в какой-то области оси Ox отличается от Fn (x) на конечную величину, а поскольку Fn (x) близка к истинной функции распределения, то в этой области отклонение | Fn (x)- F (x)| конечно, а множитель  делает критерий большим. Кроме того, по теореме Колмогорова мы приближённо знаем закон распределения.
делает критерий большим. Кроме того, по теореме Колмогорова мы приближённо знаем закон распределения.
Сформулируем процедуру проверки гипотезы H:
a) Задаём a.
b) Из таблицы распределения Колмогорова находим значение C из уравнения 2 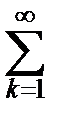 (-1) k +1 e -2 k 2 C 2=a.
(-1) k +1 e -2 k 2 C 2=a.
c) Вычисляем K: K = 
 | Fn (x)- F (x)|.
| Fn (x)- F (x)|.
d) Сравниваем K и С: если K > С, то гипотезу H отвергаем, если K £ С, то H принимаем.
Ошибку второго рода контролировать эффективно не удаётся, так как распределения критерия при гипотезе 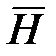 мы не знаем. Однако можно доказать, что если H не верна, то при достаточно большом n из закона больших чисел следует, что критерий K отвергнет ошибочную гипотезу со сколь угодно большой вероятностью.
мы не знаем. Однако можно доказать, что если H не верна, то при достаточно большом n из закона больших чисел следует, что критерий K отвергнет ошибочную гипотезу со сколь угодно большой вероятностью.
Недостатком критерия Колмогорова представляется то, что гипотеза должна точно задавать закон распределения F (x). На практике чаще всего известен тип закона, но неизвестны параметры. Применение критерия Колмогорова не допускает оценки параметров по той же выборке, по которой вычисляется сам критерий, – это было бы прямой подгонкой. Однако, не запрещается оценить параметры по другой выборке, после чего функция распределения F (x) становится известной, и процедура проверки может применяться.
|
|
Критерий c2 Пирсона
Пусть A 1, A 2, ¼, Ak – полная группа попарно несовместных событий, p 1, p 2, ¼, pk – их вероятности. Предположим, что в n независимых испытаниях эти события произошли, соответственно, m 1, m 2, ¼, mk раз,  mi = n. Как доказал Пирсон, в этих условиях
mi = n. Как доказал Пирсон, в этих условиях
 P
P  =
= 
 (x) dx,
(x) dx,
т.е. величина
c2= 
в пределе имеет c2-распределение с (k -1) степенями свободы.
Считаем n достаточно большим, чтобы можно было пользоваться приближённым равенством.
Теорема Пирсона лежит в основе проверки нескольких статистических гипотез.
Простейшая из них касается дискретной случайной величины X с возможными значениями x 1, x 2, ¼, xk. Гипотеза H состоит в том, что вероятности этих значений p 1, p 2, ¼, pk. Получаем выборку, которая состоит из m 1, m 2, ¼ ¼, mk раз повторившихся возможных значений x 1, x 2, ¼, xk. Применима теорема Пирсона, причём Ai ={ X = xi }, 1, 2, ¼, k. Она подсказывает, что в качестве критерия следует взять величину
K =c2=  .
.
Приближённо закон её распределения даёт теорема Пирсона. Кроме того, mi как абсолютные частоты событий Ai, подчиняются биномиальному закону:
mi ~ B (n, pi), i =1, 2, ¼, k,
Mmi = npi,
и, если гипотеза H верна, то mi» npi, так что числители в сумме c2, следует ожидать, малы, а знаменатели при достаточно большом n велики и критерий c2имеет тенденцию быть малым. Если же гипотеза H не верна, то $ i, для которого
P { X = xi }¹ pi и mi» npi ¢,
где pi ¢– истинное значение вероятности P { X = xi }. Числитель i -ого слагаемого близок к n 2(pi - pi ¢)2, а само слагаемое примерно равно 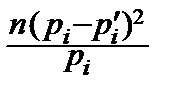 , причём
, причём 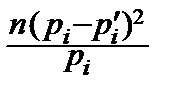
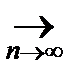 ¥. При достаточно большом n мы попадём в критическую область, поскольку критерий имеет тенденцию быть большим для неверной гипотезы.
¥. При достаточно большом n мы попадём в критическую область, поскольку критерий имеет тенденцию быть большим для неверной гипотезы.
Итак, процедура проверки гипотезы H по критерию Пирсона выглядит следующие образом:
a) Задаём уровень значимости a.
b) По таблицам c2-распределения находим пороговое значение C из уравнения 
 (x) dx =a.
(x) dx =a.
c) Вычисляем c2=  .
.
d) Сравниваем c2и C: если c2> C, то H отвергается; если c2£ C, то H принимается.
Из изложенного ясно, что все приближения, допущенные в процессе проверки, будут с большой вероятностью удовлетворительными, если для " i будут достаточно большими величины npi. Поэтому, если $ i, для которых pi слишком малы, следует проводить группировку наблюдений и соответственно менять гипотезу, присоединяя маловероятные значения xi к соседним или объединяя их вместе. Группировку наблюдений в соответствующую группировку возможных значений нужно, в частности, проводить в случае, если число возможных значений k бесконечно.
|
|
Ошибку второго рода вновь невозможно эффективно контролировать, так как, если H не верна, мы обычно не знаем, что же имеет место в действительности. Однако утешением является уверенность в том, что при достаточно большом n вероятность принять неверную гипотезу как угодно мала для сколь угодно близких альтернатив.
Критерий c2Пирсона можно применять и для проверки той же гипотезы, что и критерий Колмогорова: F (x) – функция распределения непрерывной случайной величины X. С этой целью разобьем ось Ox на интервалы D i такие, чтобы вероятности pi = P { X ÎD i } были достаточно велики (достаточно велики должны быть числа npi). Роль событий Ai играют Ai ={ X ÎD i } и проверяется гипотеза H: pi = P { X ÎD i }, " i.
Пожалуй, все критерии выглядят более убедительными, когда они отвергают гипотезу, чем когда они её принимают: первое заключение делается по событию, которое практически невероятно и всё-таки произошло, а второе – по событию, которое весьма вероятно и действительно произошло. Здесь же это различие особенно чувствуется, так как мы фактически деформировали гипотезу, заменили её её следствием, из которого сама она не следует: если следствие отвергается, то отвергается и сама гипотеза; если же следствие принимается, это еще не доказывает верности самой гипотезы.
Выбор числа интервалов и их размеры определяются тем, чтобы в интервалы попадало достаточно большое число наблюдений: работа критерия Пирсона основана на том, сколь хорошо выполняется для " i приближение mi» npi, если H справедлива, и сколь плохо выполняется оно хотя бы для некоторых i, если H не справедлива. А на это можно рассчитывать лишь при достаточно большом числе наблюдений, попавших в интервалы D i.
Как оказалось, критерием c2Пирсона можно пользоваться и в том случае, когда гипотеза задаёт закон распределения с точностью до параметров, например, в дискретном случае
H: pi = pi (q1, q2, ¼, q r), i =1, 2, ¼, k,
и r неизвестных параметров оцениваются по той же выборке, которая используется для проверки самой гипотезы.
Единственное изменение в процедуре проверки состоит в том, что в распределении c2нужно брать число степеней свободы не k -1, а k - r -1.
Критерий Стьюдента
Пусть случайная величина X распределена по нормальному закону, и проверяется гипотеза H, состоящая в том, что число a есть ни что иное, как математическое ожидание X:
H: a = MX.
Как мы установили выше, выборочное среднее и выборочная дисперсия подчиняются следующему закону:
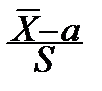 = Tn -1.
= Tn -1.
Дробь Стьюдента 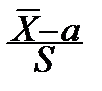 распределена по закону, носящему его имя, с n -1степенями свободы. При условии справедливости H
распределена по закону, носящему его имя, с n -1степенями свободы. При условии справедливости H
P  =
= 

 .
.
Эта теорема подсказывает выбор критерия для проверки гипотезы H:
K (x 1, x 2, ¼, xn)= 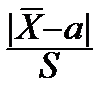 .
.
Закон его распределения нам известен, и критерий ведет себя именно так, как нужно: если гипотеза H верна, следует ожидать малых значений K, если H не верна, не следует ожидать малых значений K.
Процедура проверки такова:
a) Задаём a.
b) По таблицам распределения Стьюдента находим порог С из уравнения
 pTn -1(t) dt =
pTn -1(t) dt = 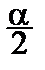 .
.
c) Вычисляем K = 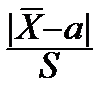 .
.
d) Сравниваем K и С: если K > С, то H отвергается; если K £ С, H принимается.
Можно видоизменить критерий Стьюдента для следующего случая: имеются две независимые нормальные случайные величины X и Y, и получены две выборки (x 1, x 2, ¼, xn) и (y 1, y 2, ¼, ym). Дисперсии равны, но неизвестны: s1=s2=s. Проверяется гипотеза H: MX = MY.
Очевидно, в условиях справедливости H:
 -
- 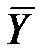 ~ N (0; s
~ N (0; s  ),
),

 (xi -
(xi -  )2~c
)2~c  ,
,

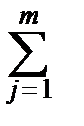 (yj -
(yj - 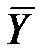 )2~c
)2~c  ,
,
 [
[  (xi -
(xi -  )2+
)2+ 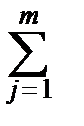 (yj -
(yj - 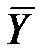 )2]~c
)2]~c 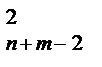 ,
,
и мы можем составить дробь Стьюдента:
 = Tn + m -2.
= Tn + m -2.
Очевидно, в качестве критерия нужно взять
K = 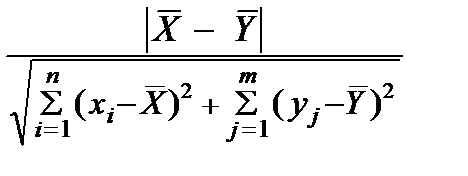

с критической областью K > С.
|
|
|

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!