Пусть X ~ F (x, q). Аналитический вид функции F (x, q) известен, но значение параметра q – неизвестно. Требуется: понаблюдав n раз X, найти q хотя бы приближённо, т. е. требуется указать такую функцию от выборки  (x 1, x 2, ¼, xn), чтобы можно было считать её приближением для q:
(x 1, x 2, ¼, xn), чтобы можно было считать её приближением для q:
q»  (x 1, x 2, ¼, xn).
(x 1, x 2, ¼, xn).
Такая функция  называется точечной оценкой параметра q. Следует учитывать, что в данной постановке задачи параметр q может быть векторным – состоять из нескольких компонент; например, нормальный закон определяется двумя параметрами: a и s.
называется точечной оценкой параметра q. Следует учитывать, что в данной постановке задачи параметр q может быть векторным – состоять из нескольких компонент; например, нормальный закон определяется двумя параметрами: a и s.
Предыдущие две задачи позволяют указать желательные свойства оценки:
1. Несмещенность:  (x 1, x 2, ¼, xn)=q.
(x 1, x 2, ¼, xn)=q.
Несмещенность эквивалентна отсутствию систематической ошибки.
2. Среднеквадратическая ошибка должна быть достаточно мала. Обычно ищут оценки, для которых  ®0 при n ®¥; для них при достаточно большом объёме выборки среднеквадратическая ошибка оценки будет как угодно мала.
®0 при n ®¥; для них при достаточно большом объёме выборки среднеквадратическая ошибка оценки будет как угодно мала.
Иногда удаётся найти такую оценку  (x 1, x 2, ¼, xn), для которой дисперсия
(x 1, x 2, ¼, xn), для которой дисперсия  минимальна по сравнению со всеми мыслимыми оценками. Такая оценка называется эффективной. Однако редко бывает так, что эффективная оценка, если она существует, имеет и достаточно простой вид, удобный для практических расчётов. Часто бывает выгоднее пользоваться неэффективными, но более простыми оценками, расплачиваясь увеличением объёма выборки.
минимальна по сравнению со всеми мыслимыми оценками. Такая оценка называется эффективной. Однако редко бывает так, что эффективная оценка, если она существует, имеет и достаточно простой вид, удобный для практических расчётов. Часто бывает выгоднее пользоваться неэффективными, но более простыми оценками, расплачиваясь увеличением объёма выборки.
Во всяком случае, при сравнении двух несмещённых оценок лучше та, у которой дисперсия меньше: она, как говорят, эффективнее другой.
3. Состоятельность: желательно, чтобы вероятность заметных отклонений  от q была достаточно мала. Это достигается, если оценка
от q была достаточно мала. Это достигается, если оценка  подчиняется закону больших чисел:
подчиняется закону больших чисел:
 P {|
P {|  -q|<e}=1, для "e>0,
-q|<e}=1, для "e>0,
т. е., если  (x 1, x 2, ¼, xn) сходится по вероятности к оцениваемому параметру. Ещё лучше, если имеет место обычная сходимость почти наверное.
(x 1, x 2, ¼, xn) сходится по вероятности к оцениваемому параметру. Ещё лучше, если имеет место обычная сходимость почти наверное.
Расскажем здесь о двух способах получения точечных оценок: о методе максимального правдоподобия и методе моментов.
Метод максимального правдоподобия Р. Фишера
Изложим этот метод отдельно для непрерывного и для дискретного случаев.
a. Пусть X – дискретная случайная величина с возможными значениями xi, вероятности которых pi (q) зависят от неизвестного параметра q; аналитический вид функций pi (q) известен. Наблюдаем X независимым образом n раз. Пусть значение xi наблюдалось mi раз. Вероятность получить ту выборку, которую мы получили, равна  (q)= L (q) – функция неизвестного параметра q. При каких-то значениях q она меньше, при других – больше. Если эта вероятность при некотором q очень мала, то, надо полагать, такая выборка и не должна обычно наблюдаться. Но мы же её получили. Можно думать, что это произошло потому, что вероятность её получить достаточно велика. Принцип максимального правдоподобия состоит в том, чтобы в качестве оценки
(q)= L (q) – функция неизвестного параметра q. При каких-то значениях q она меньше, при других – больше. Если эта вероятность при некотором q очень мала, то, надо полагать, такая выборка и не должна обычно наблюдаться. Но мы же её получили. Можно думать, что это произошло потому, что вероятность её получить достаточно велика. Принцип максимального правдоподобия состоит в том, чтобы в качестве оценки  параметра q брать то значение q, при котором вероятность L (q) нашей выборки максимальна. Функция L (q) получила название функции правдоподобия, а значение
параметра q брать то значение q, при котором вероятность L (q) нашей выборки максимальна. Функция L (q) получила название функции правдоподобия, а значение  , при котором функция правдоподобия достигает максимума, получило название оценки максимального правдоподобия параметра q. Изложенное рассуждение есть лишь эвристическое соображение, основанное на здравом смысле, а не на строгой логике, и вполне могло привести нас к неудаче. Практическое применение принципа Фишера, однако, приводит часто к весьма разумным и полезным результатам. Они-то и оправдывают этот принцип.
, при котором функция правдоподобия достигает максимума, получило название оценки максимального правдоподобия параметра q. Изложенное рассуждение есть лишь эвристическое соображение, основанное на здравом смысле, а не на строгой логике, и вполне могло привести нас к неудаче. Практическое применение принципа Фишера, однако, приводит часто к весьма разумным и полезным результатам. Они-то и оправдывают этот принцип.
b. Пусть X – непрерывная случайная величина с плотностью вероятности p (x, q). Совместная плотность вероятности выборки равна L (q)=  p (xi, q) и называется функцией правдоподобия.
p (xi, q) и называется функцией правдоподобия.
Принцип максимального правдоподобия состоит здесь в том, чтобы в качестве оценки параметра q брать точку  , в которой L (q) достигает максимума.
, в которой L (q) достигает максимума.
Сделаем несколько вычислительных замечаний.
Если L (q) – дифференцируемая функция, то поиск максимума ведётся обычными средствами анализа: ищется корень уравнения L ¢(q)=0 и проверяется, действительно ли в нём экстремум. Часто в этом случае удобнее искать максимум не функции L (q), а функции ln L (q), используя монотонность логарифма.
Если параметр q меняется в конечном отрезке, то нужно исследовать также и концы отрезка.
Если параметр q векторный, то вместо обычной производной приходится рассматривать частные производные.
Посмотрим, как действует этот метод на конкретных примерах.
1°. X ~P(l), q=l. Функция правдоподобия:
L (l)= 
 Þ ln L (l)=
Þ ln L (l)=  mk (k lnl-l-ln k!).
mk (k lnl-l-ln k!).
Лишь конечное число сомножителей в выражении L (l) отлично от единицы, так что вопрос о сходимости бесконечного произведения не встаёт.
Имеем:
 ln L (l)=0 Û
ln L (l)=0 Û  mk (
mk (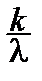 -1)=0 Û
-1)=0 Û 
 kmk -
kmk -  mk =0
mk =0
и так как  mk = n, то корнем
mk = n, то корнем  ln L (l)=0 является
ln L (l)=0 является  =
= 
 kmk =
kmk =  .
.
Т. к. L (l) при l>0 положительна и, очевидно, L (0)=0,  L (l)=0, то экстремумом L (l) может быть только максимум.
L (l)=0, то экстремумом L (l) может быть только максимум.
Поскольку параметр l пуассоновской случайной величины является её математическим ожиданием, то результат λ»  , как мы знаем, весьма хорош.
, как мы знаем, весьма хорош.
2°. X ~ B (n, p). Считаем n известным, а p параметром: q= p:
Функция правдоподобия: L (p)=  (
( pkqn - k) mk.
pkqn - k) mk.
Здесь не следует путать n с объёмом выборки, который равен  mk.
mk.
Имеем:
ln L (p)=  mk [ln
mk [ln  + k ln p +(n - k)ln(1- p)].
+ k ln p +(n - k)ln(1- p)].
Найдём корень производной функции ln L (p):
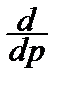 ln L (p)=0 Û
ln L (p)=0 Û  mk (
mk ( -
-  )=0.
)=0.
Корень полученного уравнения:  =
=  .
.
Мы вновь получили разумный результат, поскольку
np = MX, а  =
=  .
.
Методом максимального правдоподобия Р. Фишера нами получена та же оценка математического ожидания биномиального закона, какую бы мы написали для np – выборочное среднее.
3°. Найдём оценку максимального правдоподобия для вероятности события A: P (A)= p, q= p.
Будем считать, что n раз наблюдаются значения случайной величины
X = 
|
1, если событие
A произошло,
0, если событие
A не произошло.
Функция правдоподобия: L (p)= pm (1- p) n - m.
Имеем:
ln L (p)= m ln p +(n - m)ln(1- p) Þ 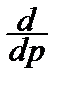 ln L (p)=0 Û
ln L (p)=0 Û  -
-  =0 Þ
=0 Þ  =
=  ,
,
 – корень уравнения. На концах отрезка [0, 1] функция L (p) обращается в ноль, а в остальных точках отрезка она положительна, так что единственная точка экстремума является точкой максимума.
– корень уравнения. На концах отрезка [0, 1] функция L (p) обращается в ноль, а в остальных точках отрезка она положительна, так что единственная точка экстремума является точкой максимума.
Таким образом, метод максимального правдоподобия советует брать в качестве оценки вероятности события A его относительную частоту, что, как мы знаем, хорошо.
4°. X ~ Exp (m), q=m.
Функция правдоподобия: L (m)=  m e -m xk, если xk ³0, и L (m)º0, если хотя бы одно из xk =0. Так как все выборочные значения xk положительны, то
m e -m xk, если xk ³0, и L (m)º0, если хотя бы одно из xk =0. Так как все выборочные значения xk положительны, то
ln L (m)= n lnm-m  xk Þ
xk Þ  ln L (m)=0 Û
ln L (m)=0 Û  -
-  xk =0 Þ
xk =0 Þ  =
=  .
.
Результат следует признать разумным, поскольку предлагается для  брать в качестве приближения
брать в качестве приближения  , а
, а  = MX.
= MX.
5°. X ~ N (a, s). Здесь параметр q состоит из двух компонент: q=(a, s).
Функция правдоподобия: L (a, s)= 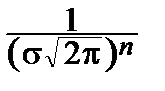 exp
exp  (-
(- 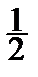
 ), откуда:
), откуда:
ln L (a, s)=- n lns- n ln 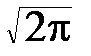 -
- 
 (xk - a)2.
(xk - a)2.
Уравнения для нахождения точки экстремума:

ln
L (
a, s)=


(
xk -
a)=0,

ln
L (
a, s)=-

+


(
xk -
a)
2=0.
Отсюда находим точку экстремума ( ,
,  ):
):  =
= 
 xk =
xk =  ,
,  =
=  .
.
Таким образом, для нормального закона в качестве оценки максимального правдоподобия мы получаем: для параметра a – выборочное среднее, а для дисперсии s2 – так называемую выборочную дисперсию (её обозначают S 2):
a»  ,s 2»
,s 2» 
 (xk -
(xk -  )2= S 2.
)2= S 2.
Легко проверить, что точка ( ,
,  ) действительно является точкой максимума функции L (a, s).
) действительно является точкой максимума функции L (a, s).
6°. X ~ R (a, b); q=(a, b).
Плотность вероятности равномерного закона:
p (x)= 
|

, если
x Î[
a,
b ],
0, если
x Ï[
a,
b ].
Функция правдоподобия:
L (a, b)= 
|

, "
xk Î[
a,
b ],
0, если
xk Ï[
a,
b ].
Здесь мы имеем случай, когда максимум достигается не в корне производной, а в точке разрыва функции правдоподобия. Ясно, что максимум может достигаться лишь в случае, когда все наблюдения xk находятся в промежутке [ a, b ], а при этом выражение  тем больше, чем ближе b к a, но сближать a и b можно лишь не выпуская все наблюдения из отрезка [ a, b ]. Следовательно, max L (a, b) достигается при
тем больше, чем ближе b к a, но сближать a и b можно лишь не выпуская все наблюдения из отрезка [ a, b ]. Следовательно, max L (a, b) достигается при  =
=  xk,
xk,  =
=  xk.
xk.
7°. Пусть Х имеет гамма-распределение: X ~G(l, m), (l>0, m>0). Плотность распределения: p (x)= 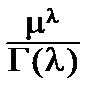 x l-1 e -m x, при x ³0; q=(l, m).
x l-1 e -m x, при x ³0; q=(l, m).
Функция правдоподобия:
L (l, m)=  [
[ 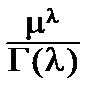 xk l-1 e -m xk ], " xk >0,
xk l-1 e -m xk ], " xk >0,
её логарифм:
ln L (l, m)= 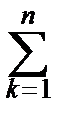 [llnm+(l-1)ln xk -m xk -lnG(l)].
[llnm+(l-1)ln xk -m xk -lnG(l)].
Уравнения максимального правдоподобия:

ln
L =
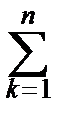
[lnm+ln
xk -y(l)]=0,
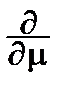
ln
L =
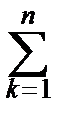
(

-
xk)=0,
где y(l)=  lnG(l) – логарифмическая производная гамма-функции, так что для оценок получаем систему двух уравнений:
lnG(l) – логарифмическая производная гамма-функции, так что для оценок получаем систему двух уравнений:
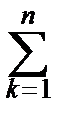
ln
xk =
n [y(l)-lnm],

=

,
и качество оценок уже не столь очевидно, как в предыдущих случаях.
Перейдем теперь к методу моментов.
Метод моментов
Пусть X ~ F (x, q1, q2, ¼, q r), причём аналитический вид функции распределения случайной величины X известен. Для нахождения r неизвестных параметров нужно иметь r уравнений. Мы знаем, что хорошим приближением для функции распределения оказывается эмпирическая функция распределения: Fn (x)» F (x). Можно надеяться, что и числовые характеристики этих функций также близки друг к другу, в частности, близки моменты. Эмпирическая функция распределения представляет собой закон распределения дискретной случайной величины, возможные значения которой совпадают с выборочными значениями xi, а вероятности их равны  , в частности, для непрерывной случайной величины X с вероятностью 1 эти вероятности равны
, в частности, для непрерывной случайной величины X с вероятностью 1 эти вероятности равны  . Выражения для моментов эмпирической функции распределения Fn (x) (их называют выборочными моментами) нетрудно написать:
. Выражения для моментов эмпирической функции распределения Fn (x) (их называют выборочными моментами) нетрудно написать:
ml = 
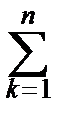 xkl, m l =
xkl, m l = 
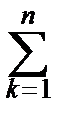 (xk -
(xk -  ) l.
) l.
Необходимые нам уравнения для нахождения параметров q1, q2, ¼, q r мы получим, приравнивая соответствующие моменты случайной величины X моментам распределения Fn (x):
ml (q1, q2, ¼, q r)= 
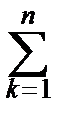 xkl, l =1, 2, ¼, r ( ,*)
xkl, l =1, 2, ¼, r ( ,*)
или:
m l(q
1, q
2, ¼, q
r)=

,
m
l (q
1, q
2, ¼, q
r)=

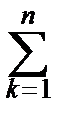
(
xk -

)
l,
l =1, 2, ¼,
r.
Успех этого метода в значительной степени зависит от того, сколь сложной оказывается соответствующая система уравнений ((*) или (**)). Решения системы и берутся в качестве оценок  ,
, 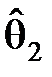 , ¼,
, ¼,  r для параметров q1, q2, ¼, q r.
r для параметров q1, q2, ¼, q r.
Например, для нормального закона система (**) имеет вид:
a =  ,
,
s2= 
 (xk -
(xk -  )2= S 2,
)2= S 2,
что совпадает с оценкой максимального правдоподобия, и это подтверждает разумность идеи.
Вообще, для произвольной случайной величины по методу моментов для математического ожидания – первого начального момента – мы получаем
MX»  ,
,
а для дисперсии – второго центрального момента:
DX» 
 (xk -
(xk -  )2= S 2,
)2= S 2,
т. е. выборочную дисперсию. Первая оценка, как мы уже знаем, несмещенная, состоятельная, с дисперсией  =
=  DX, которая при n ®¥ сколь угодно мала. А второй оценкой займёмся здесь. В частности, обнаружим, что она имеет смещение, т. е. имеет систематическую погрешность.
DX, которая при n ®¥ сколь угодно мала. А второй оценкой займёмся здесь. В частности, обнаружим, что она имеет смещение, т. е. имеет систематическую погрешность.
С этой целью вычислим MS 2:
MS 2= M { 
 [(xk - MX)-(
[(xk - MX)-( - MX)]2}=
- MX)]2}=
= 
 M [(xk - MX)2]-
M [(xk - MX)2]-  M [(
M [( - MX)
- MX)  (xk - MX)]+
(xk - MX)]+  M [(
M [( - MX)2]=
- MX)2]=
=  × n × DX -2 M [(
× n × DX -2 M [( - MX)2]+ M [(
- MX)2]+ M [( - MX)2]= DX -
- MX)2]= DX -  = DX -
= DX -  DX =
DX =  DX.
DX.
Итак, MS 2=  DX, что указывает на смещённость S 2 как оценки для DX. Однако множитель
DX, что указывает на смещённость S 2 как оценки для DX. Однако множитель  для больших n близок к единице, и смещение асимптотически исчезает. Практики часто этой систематической ошибкой пренебрегают. Нетрудно её полностью исключить, если переписать последнее равенство в таком виде:
для больших n близок к единице, и смещение асимптотически исчезает. Практики часто этой систематической ошибкой пренебрегают. Нетрудно её полностью исключить, если переписать последнее равенство в таком виде:
M ( S 2)= DX,
S 2)= DX,
т.е. несмещенная оценка для дисперсии (обозначим её s 2) равна
s 2=  S 2=
S 2= 
 (xk -
(xk -  )2.
)2.
Вся поправка состоит лишь в том, чтобы делить сумму квадратов на число наблюдений без единицы.
Вместе с тем, этот пример показывает, что ни метод максимального правдоподобия, ни метод моментов не гарантируют несмещённости их оценок.
Отметим полезное тождество:
nS 2=(n -1) s 2=  (xk -
(xk -  )2.
)2.
Мы решили здесь как частный случай задачу IV: нашли точечную несмещённую оценку дисперсии случайной величины X, имеющей дисперсию:
DX» s 2= 
 (xk -
(xk -  )2.
)2.
V. ГРУППИРОВКА НАБЛЮДЕНИЙ
Если объём выборки очень велик, то обрабатывать весь массив собранных данных бывает иногда затруднительно. С целью облегчить вычислительную работу в таких случаях производят так называемую группировку наблюдений. Она бывает также необходима для некоторых статистических процедур.
Представим выборку (x 1, x 2, ¼, xn) в виде вариационного ряда: y 1£ y 2£
£¼£ yn. Величина yn - y 1 называется размахом выборки. Разобьём отрезок [ y 1, yn ] на N равных частей длины D=  .
.
Поскольку неизбежно округление данных, следует договориться о концах интервалов: разбиваем весь отрезок [ y 1, yn ] на отрезки
D k =[ xk o-  , xk o+
, xk o+  ),
),
где xk o– середина k -ого полузакрытого интервала. При таком разбиении последний интервал берём в виде
D N =[ xN o-  , xN o+
, xN o+  ].
].
Обозначим через mk число наблюдений, попавших в k -й интервал D k. Числа x 1o< x 2o<¼< xN o называют интервальным вариационным рядом, mk – приписанные этим точкам частоты.
В принципе, можно строить интервальный вариационный ряд, производя, если это нужно, разбиение и на неравные интервалы.
Вся дальнейшая работа (например, построение эмпирической функции распределения, оценки и т. д.) осуществляется уже с интервальным вариационным рядом. При этом нужно не забывать, что группировка вносит в статистические вычисления дополнительную ошибку – ошибку на группировку.
Число интервалов N выбирают так, чтобы частоты mk были достаточно велики, а само число N не слишком велико.
Разбиение на неравные интервалы производят в том случае, если на оси x есть области очень бедные попавшими туда наблюдениями.



 (x 1, x 2, ¼, xn), чтобы можно было считать её приближением для q:
(x 1, x 2, ¼, xn), чтобы можно было считать её приближением для q: (x 1, x 2, ¼, xn)=q.
(x 1, x 2, ¼, xn)=q. ®0 при n ®¥; для них при достаточно большом объёме выборки среднеквадратическая ошибка оценки будет как угодно мала.
®0 при n ®¥; для них при достаточно большом объёме выборки среднеквадратическая ошибка оценки будет как угодно мала. P {|
P {|  (q)= L (q) – функция неизвестного параметра q. При каких-то значениях q она меньше, при других – больше. Если эта вероятность при некотором q очень мала, то, надо полагать, такая выборка и не должна обычно наблюдаться. Но мы же её получили. Можно думать, что это произошло потому, что вероятность её получить достаточно велика. Принцип максимального правдоподобия состоит в том, чтобы в качестве оценки
(q)= L (q) – функция неизвестного параметра q. При каких-то значениях q она меньше, при других – больше. Если эта вероятность при некотором q очень мала, то, надо полагать, такая выборка и не должна обычно наблюдаться. Но мы же её получили. Можно думать, что это произошло потому, что вероятность её получить достаточно велика. Принцип максимального правдоподобия состоит в том, чтобы в качестве оценки  p (xi, q) и называется функцией правдоподобия.
p (xi, q) и называется функцией правдоподобия.
 Þ ln L (l)=
Þ ln L (l)=  mk (k lnl-l-ln k!).
mk (k lnl-l-ln k!). ln L (l)=0 Û
ln L (l)=0 Û 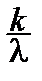 -1)=0 Û
-1)=0 Û 
 =
= 
 .
. L (l)=0, то экстремумом L (l) может быть только максимум.
L (l)=0, то экстремумом L (l) может быть только максимум. (
( pkqn - k) mk.
pkqn - k) mk. mk.
mk.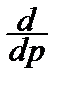 ln L (p)=0 Û
ln L (p)=0 Û  -
-  )=0.
)=0. =
=  .
. =
= 
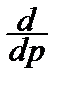 ln L (p)=0 Û
ln L (p)=0 Û  -
-  =0 Þ
=0 Þ  ,
, m e -m xk, если xk ³0, и L (m)º0, если хотя бы одно из xk =0. Так как все выборочные значения xk положительны, то
m e -m xk, если xk ³0, и L (m)º0, если хотя бы одно из xk =0. Так как все выборочные значения xk положительны, то xk Þ
xk Þ  ln L (m)=0 Û
ln L (m)=0 Û  -
-  =
=  .
. брать в качестве приближения
брать в качестве приближения 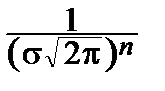 exp
exp 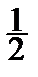
 ), откуда:
), откуда: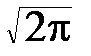 -
- 

 ln L (a, s)=
ln L (a, s)= 
 ln L (a, s)=-
ln L (a, s)=-  +
+ 
 ,
,  ):
):  .
. , если x Î[ a, b ],
, если x Î[ a, b ],
 , " xk Î[ a, b ],
, " xk Î[ a, b ], xk,
xk,  =
=  xk.
xk.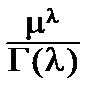 x l-1 e -m x, при x ³0; q=(l, m).
x l-1 e -m x, при x ³0; q=(l, m).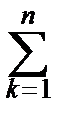 [llnm+(l-1)ln xk -m xk -lnG(l)].
[llnm+(l-1)ln xk -m xk -lnG(l)].
 ln L =
ln L = 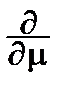 ln L =
ln L =  - xk)=0,
- xk)=0,
 lnG(l) – логарифмическая производная гамма-функции, так что для оценок получаем систему двух уравнений:
lnG(l) – логарифмическая производная гамма-функции, так что для оценок получаем систему двух уравнений:
 , в частности, для непрерывной случайной величины X с вероятностью 1 эти вероятности равны
, в частности, для непрерывной случайной величины X с вероятностью 1 эти вероятности равны  . Выражения для моментов эмпирической функции распределения Fn (x) (их называют выборочными моментами) нетрудно написать:
. Выражения для моментов эмпирической функции распределения Fn (x) (их называют выборочными моментами) нетрудно написать:
 ,
,  , ¼,
, ¼,  r для параметров q1, q2, ¼, q r.
r для параметров q1, q2, ¼, q r.
 =
=  M [(
M [( M [(
M [( = DX -
= DX -  DX.
DX. S 2)= DX,
S 2)= DX,
 .
. , xk o+
, xk o+