Математическая статистика
ВВОДНЫЕ ЗАМЕЧАНИЯ
В теории вероятностей о вероятностях, законах распределения, параметрах случайных величин говорится как о чём-то данном, известном. Но встаёт вопрос: откуда их взять? Как найти параметры хотя бы приближённо? Как проверить предположение о том, что некоторая случайная величина распределена, например, по нормальному закону?
На эти и подобные им вопросы отвечает математическая статистика, причём информацию для ответов она берёт из наблюдений над случайными событиями и величинами. При этом наблюдения ведутся над реальными объектами и моделями, тогда как теория вероятностей изучает математические модели, в значительной степени идеализированные и абстрагированные. Соотношение между выводами математической теории и поведением реального мира приобретает уже не философский, а практический смысл. Можно сказать, что математическая статистика заведует связями теории вероятностей с внешним миром.
Ниже мы будем рассматривать одну единственную статистическую модель: предполагается, что существует случайная величина X, которую можно наблюдать повторно n раз в независимых опытах. Результатом таких наблюдений оказываются n значений, которые X приняла в n экспериментах: (x 1, x 2, ¼ ¼, xn), – так называемая выборка, n – объём выборки. На все вопросы о случайной величине X математическая статистика берётся отвечать по выборке.
В каждом опыте мы наблюдаем одну и ту же случайную величину X; все опыты по предположению независимы. Можно считать, что фактически мы наблюдаем n - мерную случайную величину (X 1, X 2, ¼, Xn) с независимыми компонентами, распределёнными одинаково – по тому же закону, что и X. Выборка (x 1, x 2, ¼, xn) есть наблюдённое значение случайной величины (X 1, X 2, ¼, Xn), выборка – одно из её возможных значений; её можно представить точкой в n -мерном евклидовом пространстве. Всё множество точек, которые могут быть выборками, образует так называемое выборочное пространство. По сути дела выборка – элементарное событие, а выборочное пространство – пространство элементарных событий W. Часто смотрят на выборку (x 1, x 2, ¼, xn) как на случайную величину и не вводят особого обозначения (X 1, X 2, ¼, Xn) для случайной величины.
Если X ~ N (a, s), то выборочным пространством оказывается всё евклидово пространство Rn. Если X ~P(l), то выборочное пространство совпадает с целочисленной решёткой главного координатного угла. Если X ~ R (0, 1), то W – единичный n -мерный куб.
Пусть X ~ F (x, q): F (x, q) – функция распределения случайной величины X. Тогда совместная функция распределения выборки:
F (x 1, x 2, ¼, xn)=  F (xi, q).
F (xi, q).
Если X имеет плотность вероятности p (x, q), то совместная плотность вероятности выборки равна
p (x 1, x 2, ¼, xn)=  p (xi, q).
p (xi, q).
Познакомимся с важнейшими задачами математической статистики и с их статистическими решениями.
V. ГРУППИРОВКА НАБЛЮДЕНИЙ
Если объём выборки очень велик, то обрабатывать весь массив собранных данных бывает иногда затруднительно. С целью облегчить вычислительную работу в таких случаях производят так называемую группировку наблюдений. Она бывает также необходима для некоторых статистических процедур.
Представим выборку (x 1, x 2, ¼, xn) в виде вариационного ряда: y 1£ y 2£
£¼£ yn. Величина yn - y 1 называется размахом выборки. Разобьём отрезок [ y 1, yn ] на N равных частей длины D=  .
.
Поскольку неизбежно округление данных, следует договориться о концах интервалов: разбиваем весь отрезок [ y 1, yn ] на отрезки
D k =[ xk o-  , xk o+
, xk o+  ),
),
где xk o– середина k -ого полузакрытого интервала. При таком разбиении последний интервал берём в виде
D N =[ xN o-  , xN o+
, xN o+  ].
].
Обозначим через mk число наблюдений, попавших в k -й интервал D k. Числа x 1o< x 2o<¼< xN o называют интервальным вариационным рядом, mk – приписанные этим точкам частоты.
В принципе, можно строить интервальный вариационный ряд, производя, если это нужно, разбиение и на неравные интервалы.
Вся дальнейшая работа (например, построение эмпирической функции распределения, оценки и т. д.) осуществляется уже с интервальным вариационным рядом. При этом нужно не забывать, что группировка вносит в статистические вычисления дополнительную ошибку – ошибку на группировку.
Число интервалов N выбирают так, чтобы частоты mk были достаточно велики, а само число N не слишком велико.
Разбиение на неравные интервалы производят в том случае, если на оси x есть области очень бедные попавшими туда наблюдениями.
Математическая статистика
ВВОДНЫЕ ЗАМЕЧАНИЯ
В теории вероятностей о вероятностях, законах распределения, параметрах случайных величин говорится как о чём-то данном, известном. Но встаёт вопрос: откуда их взять? Как найти параметры хотя бы приближённо? Как проверить предположение о том, что некоторая случайная величина распределена, например, по нормальному закону?
На эти и подобные им вопросы отвечает математическая статистика, причём информацию для ответов она берёт из наблюдений над случайными событиями и величинами. При этом наблюдения ведутся над реальными объектами и моделями, тогда как теория вероятностей изучает математические модели, в значительной степени идеализированные и абстрагированные. Соотношение между выводами математической теории и поведением реального мира приобретает уже не философский, а практический смысл. Можно сказать, что математическая статистика заведует связями теории вероятностей с внешним миром.
Ниже мы будем рассматривать одну единственную статистическую модель: предполагается, что существует случайная величина X, которую можно наблюдать повторно n раз в независимых опытах. Результатом таких наблюдений оказываются n значений, которые X приняла в n экспериментах: (x 1, x 2, ¼ ¼, xn), – так называемая выборка, n – объём выборки. На все вопросы о случайной величине X математическая статистика берётся отвечать по выборке.
В каждом опыте мы наблюдаем одну и ту же случайную величину X; все опыты по предположению независимы. Можно считать, что фактически мы наблюдаем n - мерную случайную величину (X 1, X 2, ¼, Xn) с независимыми компонентами, распределёнными одинаково – по тому же закону, что и X. Выборка (x 1, x 2, ¼, xn) есть наблюдённое значение случайной величины (X 1, X 2, ¼, Xn), выборка – одно из её возможных значений; её можно представить точкой в n -мерном евклидовом пространстве. Всё множество точек, которые могут быть выборками, образует так называемое выборочное пространство. По сути дела выборка – элементарное событие, а выборочное пространство – пространство элементарных событий W. Часто смотрят на выборку (x 1, x 2, ¼, xn) как на случайную величину и не вводят особого обозначения (X 1, X 2, ¼, Xn) для случайной величины.
Если X ~ N (a, s), то выборочным пространством оказывается всё евклидово пространство Rn. Если X ~P(l), то выборочное пространство совпадает с целочисленной решёткой главного координатного угла. Если X ~ R (0, 1), то W – единичный n -мерный куб.
Пусть X ~ F (x, q): F (x, q) – функция распределения случайной величины X. Тогда совместная функция распределения выборки:
F (x 1, x 2, ¼, xn)=  F (xi, q).
F (xi, q).
Если X имеет плотность вероятности p (x, q), то совместная плотность вероятности выборки равна
p (x 1, x 2, ¼, xn)=  p (xi, q).
p (xi, q).
Познакомимся с важнейшими задачами математической статистики и с их статистическими решениями.
I. ОТНОСИТЕЛЬНАЯ ЧАСТОТА КАК ОЦЕНКА ВЕРОЯТНОСТИ
Пусть имеется событие A, вероятность которого P (A)= p – неизвестна, и мы хотим найти её хотя бы приблизительно. Из курса теории вероятностей ответ нам известен: хорошим приближением для вероятности является относительная частота события. Если в n независимых опытах событие A произошло m раз, то P (A)»  . При этом:
. При этом:
1. В среднем мы не ошибаемся: M ( )» p.
)» p.
Это свойство оценки называется несмещённостью.
2. Дисперсия оценки как угодно мала при достаточно большом числе опытов: D ( )=
)= 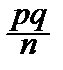 ®0 при n ®¥.
®0 при n ®¥.
Дисперсия играет роль среднего квадрата ошибки.
3. Вероятность заметных отклонений относительной частоты от вероятности мала, поскольку по закону больших чисел Бернулли:
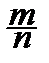
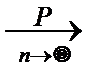 p Û
p Û 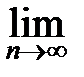 P {|
P {| 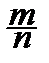 - p |<e}=1 для "e>0.
- p |<e}=1 для "e>0.
Это свойство оценки называется состоятельностью. Оно может быть усилено, поскольку по закону больших чисел Бореля:
P { 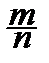 ® p }=1.
® p }=1.
Итак, относительная частота – несмещённая, состоятельная оценка для вероятности со сколь угодно малой среднеквадратической ошибкой.
Решение I задачи, таким образом, нам известно, и оно послужит нам удобным образцом для более сложных задач.
Разумеется, нужно понимать, что полученный ответ точно укладывается в рамки той единственной модели, которую мы взялись изучать в математической статистике.
Можно считать, что мы имеем здесь дело с биномиальной случайной величиной X, а выборка состоит из одного наблюдения m. Либо можно считать, что мы имеем дело здесь со случайной величиной Х=
1, если событие A произошло,
0, если событие A не произошло.
Очевидно, X – дискретная случайная величина с двумя возможными значениями 1 и 0, а вероятности этих значений p и q =1- p. Мы уже встречались с подобной величиной и выяснили, что MX = p, DX = pq.
Соответственно выборка (x 1, x 2, ¼, xn) состоит из m единиц и n - m нулей, выборочное пространство состоит из вершин n -мерного единичного куба, и
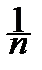 (x 1+ x 2+¼+ xn)=
(x 1+ x 2+¼+ xn)= 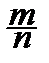 ,
,
так что ответ мы действительно получаем в терминах выборки:
p = P (A)» 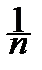 (x 1+ x 2+¼+ xn)=
(x 1+ x 2+¼+ xn)=  =
= 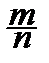 .
.
II. ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
КАК ОЦЕНКА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Пусть функция распределения случайной величины X неизвестна. Обозначим её F (x). Требуется хотя бы приблизительно её найти. Получим выборку (x 1, x 2, ¼, xn) и по ней построим так называемую эмпирическую функцию распределения:
Fn (x)= 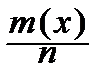 , -¥< x <+¥,
, -¥< x <+¥,
где m (x) – число наблюдений в выборке, оказавшихся меньше x.
Убедимся в том, что эмпирическая функция распределения – хорошее приближение для F (x).
Расположим наблюдения в порядке возрастания, причём повторяющиеся наблюдения выпишем лишь один раз: получим возрастающую последовательность y 1< y 2<¼< yr, называемую вариационным рядом; члены её называются порядковыми статистиками. Так, y 1= 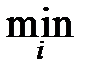 xi – минимальная порядковая статистика – первый член вариационного ряда; yr =
xi – минимальная порядковая статистика – первый член вариационного ряда; yr = 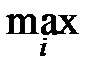 xi – максимальная порядковая статистика – последний член вариационного ряда. Пусть частота значения yi равна mi. Тогда очевидно:
xi – максимальная порядковая статистика – последний член вариационного ряда. Пусть частота значения yi равна mi. Тогда очевидно:
0, если x £ y 1,
Fn(X)= 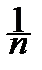
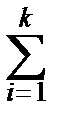 mi, если yk < x £ yk +1, k =1, 2, ¼, r -1,
mi, если yk < x £ yk +1, k =1, 2, ¼, r -1,
1, если x > yr.
Fn (x)= 
|
В частности, если все наблюдения различны (так будет, например, почти наверное для непрерывной случайной величины
X), то вариационный ряд состоит из
n порядковых статистик и
0, если x £ y 1,
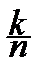 , если yk < x £ yk +1, k =1, 2, ¼, n -1,
, если yk < x £ yk +1, k =1, 2, ¼, n -1,
1, если x > yn.
Очевидно, Fn (x) – ступенчатая неотрицательная монотонная функция, имеющая разрывы в точках yi, где она совершает скачки величины  . Она обладает всеми свойствами функции распределения и задаёт закон распределения дискретной случайной величины с возможными значениями yi и вероятностями
. Она обладает всеми свойствами функции распределения и задаёт закон распределения дискретной случайной величины с возможными значениями yi и вероятностями  . Она и решает нашу задачу приближённого описания F (x).
. Она и решает нашу задачу приближённого описания F (x).
Действительно, рассмотрим событие A ={ X < x }.
Его вероятность P (A)= P { X < x }= F (x), его абсолютная частота m = m (x), его относительная частота равна Fn (x), и мы свели рассматриваемую II задачу к I, ответ на которую мы уже знаем.
Следовательно, для любого x эмпирическая функция распределения Fn (x) приближённо равна F (x), причём Fn (x) обладает следующими свойствами:
1. MFn (x)= F (x), т. е. Fn (x) – несмещённая оценка F (x);
2. DFn (x)= 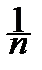 { F (x)[1- F (x)]}
{ F (x)[1- F (x)]} 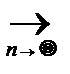 0;
0;
3. Fn (x) 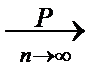 F (x) Û
F (x) Û  P {| Fn (x)- F (x)|<e}=1, "e>0. И даже:
P {| Fn (x)- F (x)|<e}=1, "e>0. И даже:
P { Fn (x) 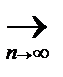 F (x)}=1 – состоятельность оценки Fn (x).
F (x)}=1 – состоятельность оценки Fn (x).
Итак, эмпирическая функция распределения Fn (x) для любого x – несмещённая, состоятельная оценка F (x) со сколь угодно малой среднеквадратической ошибкой.
III. СРЕДНЕЕ ВЫБОРОЧНОЕ КАК ОЦЕНКА
МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
Требуется по выборке (x 1, x 2, ¼, xn) оценить (т. е. приближённо найти) MX. Ответ нам уже известен: хорошим приближением для среднего значения случайной величины является среднее арифметическое наблюдений:
MX»  =
= 
 xi.
xi.
Очевидно, мы можем пользоваться теоремами о среднем арифметическом, применяя их к нашей выборке – последовательности одинаково распределённых независимых случайных величин.
Будем предполагать, что X имеет MX = a, и DX =s2.
1. В среднем мы не ошибаемся, поскольку 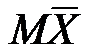 = a (имеет место несмещённость).
= a (имеет место несмещённость).
2. Среднеквадратическая ошибка приближения как угодно мала при n ®¥, поскольку 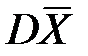 =
= 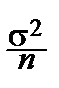 ®0.
®0.
3.  подчиняется закону больших чисел Чебышёва:
подчиняется закону больших чисел Чебышёва:

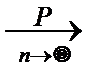 a, т. е.
a, т. е.  P {|
P {|  - a |<e}=1, "e>0,
- a |<e}=1, "e>0,
следовательно имеет место состоятельность.
В статистике принято  называть средним выборочным. Таким образом, среднее выборочное – несмещённая состоятельная оценка для математического ожидания со сколь угодно малой дисперсией при достаточно большом объёме выборки.
называть средним выборочным. Таким образом, среднее выборочное – несмещённая состоятельная оценка для математического ожидания со сколь угодно малой дисперсией при достаточно большом объёме выборки.



 F (xi, q).
F (xi, q). .
. , xk o+
, xk o+  . При этом:
. При этом: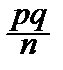 ®0 при n ®¥.
®0 при n ®¥.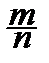
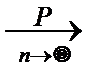 p Û
p Û 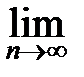 P {|
P {| 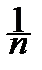 (x 1+ x 2+¼+ xn)=
(x 1+ x 2+¼+ xn)=  =
= 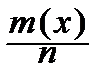 , -¥< x <+¥,
, -¥< x <+¥,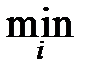 xi – минимальная порядковая статистика – первый член вариационного ряда; yr =
xi – минимальная порядковая статистика – первый член вариационного ряда; yr = 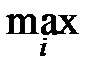 xi – максимальная порядковая статистика – последний член вариационного ряда. Пусть частота значения yi равна mi. Тогда очевидно:
xi – максимальная порядковая статистика – последний член вариационного ряда. Пусть частота значения yi равна mi. Тогда очевидно: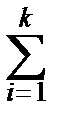 mi, если yk < x £ yk +1, k =1, 2, ¼, r -1,
mi, если yk < x £ yk +1, k =1, 2, ¼, r -1,
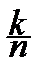 , если yk < x £ yk +1, k =1, 2, ¼, n -1,
, если yk < x £ yk +1, k =1, 2, ¼, n -1, . Она обладает всеми свойствами функции распределения и задаёт закон распределения дискретной случайной величины с возможными значениями yi и вероятностями
. Она обладает всеми свойствами функции распределения и задаёт закон распределения дискретной случайной величины с возможными значениями yi и вероятностями 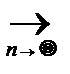 0;
0;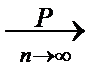 F (x) Û
F (x) Û  P {| Fn (x)- F (x)|<e}=1, "e>0. И даже:
P {| Fn (x)- F (x)|<e}=1, "e>0. И даже: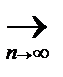 F (x)}=1 – состоятельность оценки Fn (x).
F (x)}=1 – состоятельность оценки Fn (x).
 xi.
xi.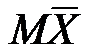 = a (имеет место несмещённость).
= a (имеет место несмещённость).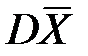 =
= 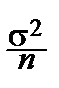 ®0.
®0.


