1. Моменты инерции
Моменты инерции части поверхности относительно осей координат выражаются поверхностными интегралами
 ,
, 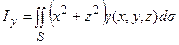 ,
,
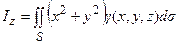 . (3.5)
. (3.5)
2. Координаты центра тяжести
Координаты центра тяжести части поверхности вычисляются по формулам:
 ,
,  ,
,
 . (3.6)
. (3.6)
Пример 3.1. Вычислить моменты инерции относительно осей координат для поверхности цилиндра
х 2 + у 2 = 9, z = 0, z = 3
с поверхностной плотностью g(х, у) = х 2 + у 2.
Решение. Воспользуемся формулами (3.5). Известно, что момент инерции тела равен сумме моментов инерции его частей, поэтому для всей поверхности цилиндра
I = I 1 + I 2 + I 3,
где I 1, I 2, I 3 - моменты инерции оснований и боковой поверхности.
1) Рассмотрим основание цилиндра, лежащее в плоскости xOy, т.е. z = 0. Здесь поверхность S 1 совпадает с двумерной областью D, т.е. элемент поверхности равен d s= dxdy. Таким образом, поверхностный интеграл обращается в двойной:
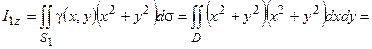
 .
.
Перейдем к полярным координатам: 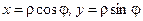 , тогда область интегрирования D будет определяться неравенствами:
, тогда область интегрирования D будет определяться неравенствами: 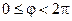 ,
,  . Момент инерции:
. Момент инерции:
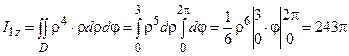 .
.
Для оси Ох:

 .
.
Основание симметрично относительно оси Oz, поэтому  .
.
2) Для основания цилиндра, лежащего в плоскости z = 3, рассуждения аналогичны.
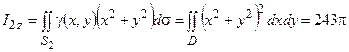 .
.
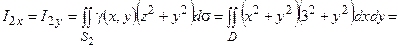
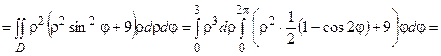
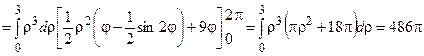
3) Боковую поверхность цилиндра зададим параметрически: 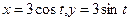 , z = z. Тогда поверхностный интеграл будем вычислять по формуле (3.4). Новыми переменными являются t и z.
, z = z. Тогда поверхностный интеграл будем вычислять по формуле (3.4). Новыми переменными являются t и z.
 ,
,
 ,
,
 .
.
Тогда 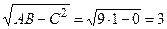 и ds =3 dt dz.
и ds =3 dt dz.
Область интегрирования D: 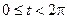 ,
,  .
.
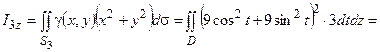
= 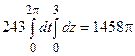 .
.



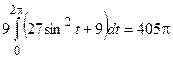 .
.
4) Моменты инерции всей поверхности находятся как суммы соответствующих моментов частей поверхности:
 .
.
 .
.
Ответ: моменты инерции поверхности равны
Ix= 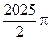 , Iy=
, Iy= 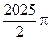 , Iz= 1944p.
, Iz= 1944p.
Пример 3.2. Найти координаты центра тяжести поверхности S, заданной уравнениями 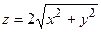 и z = 4, если поверхностная плотность
и z = 4, если поверхностная плотность 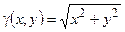 .
.
Решение. Поверхность состоит из двух частей: основания S 1 и боковой поверхности S 2. Из механики известно, что координаты центра тяжести (xc, yc, zc) всей поверхности определяются через координаты центров тяжести его частей (xci, yci, zci) следующим образом:
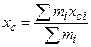 ,
,
 ,
,  ,
,
где mi - масса i -ой части поверхности.
Так как тело симметрично относительно оси Oz, то xc = = yc = 0. Аппликату центра тяжести найдем из соотношения:
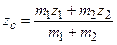 .
.
1) Найдем массу основания S 1 по формуле (3.2). Так как основание лежит в плоскости параллельной хОу, то элемент поверхности d s= dxdy и поверхностный интеграл обращается в двойной, где область интегрирования D есть проекция основания:
 .
.
Перейдем к полярным координатам:  , тогда область интегрирования D будет определяться неравенствами:
, тогда область интегрирования D будет определяться неравенствами: 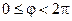 ,
, 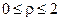 .
.
 .
.
Найдем zc 1 по формуле (3.6), учитывая, что z = 4:
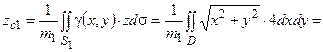
= 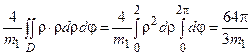 .
.
2) Боковая поверхность S 2 определяется уравнением 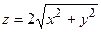 , тогда из (3.3) следует, что элемент поверхности
, тогда из (3.3) следует, что элемент поверхности


 .
.
Масса боковой поверхности:

=  .
.
Аппликата z с2:

 .
.
3) Для всей поверхности:

=  .
.
Ответ: координаты центра тяжести поверхности:
 .
.
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
ВТОРОГО РОДА
Пусть в каждой точке поверхности S определен некоторый вектор или задано векторное поле
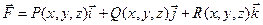 ,
,
где P, Q, R - непрерывные функции, и пусть  - единичный вектор нормали к поверхности.
- единичный вектор нормали к поверхности.
Определение. Предел интегральных сумм

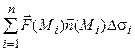
при стремлении максимального диаметра площадок Ds i к нулю называется поверхностным интегралом второго рода или поверхностным интегралом от векторной функции,
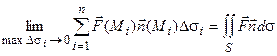 .
.
Координаты единичного вектора нормали есть направляющие косинусы, т.е.
 ,
,
тогда скалярное произведение можно расписать через координаты
 .
.
Произведение ∆σ ·cosα есть проекция площадки ∆σ на плоскость yOz, т.е. ∆σ yz. Аналогично получим остальные проекции,
 .
.
Суммируя и переходя к пределу, запишем поверхностный интеграл второго рода в другом виде, по координатам
 , (3.7)
, (3.7)
где S + - сторона поверхности, задаваемая направлением нормали  .
.
При переходе к другой стороне S - поверхности S интеграл второго рода меняет знак на противоположный.



 ,
, 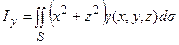 ,
,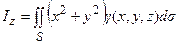 . (3.5)
. (3.5) ,
,  ,
, . (3.6)
. (3.6)
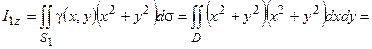
 .
.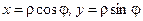 , тогда область интегрирования D будет определяться неравенствами:
, тогда область интегрирования D будет определяться неравенствами: 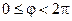 ,
,  . Момент инерции:
. Момент инерции: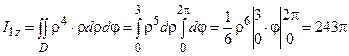 .
.
 .
. .
.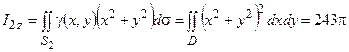 .
.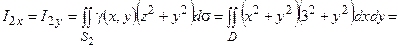
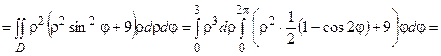
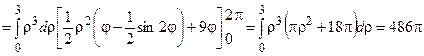
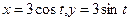 , z = z. Тогда поверхностный интеграл будем вычислять по формуле (3.4). Новыми переменными являются t и z.
, z = z. Тогда поверхностный интеграл будем вычислять по формуле (3.4). Новыми переменными являются t и z. ,
,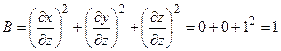 ,
, .
.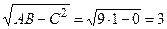 и ds =3 dt dz.
и ds =3 dt dz.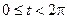 ,
,  .
.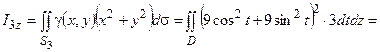
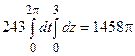 .
.


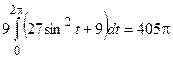 .
. .
. .
.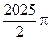 , Iy=
, Iy= 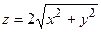 и z = 4, если поверхностная плотность
и z = 4, если поверхностная плотность 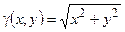 .
.
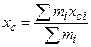 ,
, ,
,  ,
,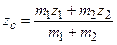 .
. .
. , тогда область интегрирования D будет определяться неравенствами:
, тогда область интегрирования D будет определяться неравенствами: 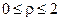 .
. .
.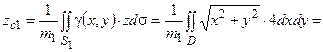
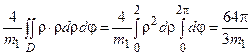 .
.

 .
.
 .
.
 .
.
 .
. .
.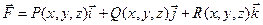 ,
, - единичный вектор нормали к поверхности.
- единичный вектор нормали к поверхности.
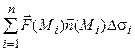
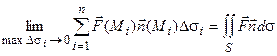 .
. ,
, .
. .
. , (3.7)
, (3.7)


