

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Анализ ошибок, возникающих при использовании методов прогноза и коррекции, удобно провести в несколько приемов.
Сначала рассмотрим ошибки ограничения прогноза (6.24) и коррекции (6.25). Результаты этого анализа выразятся через величины, уже вычисленные в процессе нахождения решения.
Затем рассмотрим вопрос выбора шага интегрирования h и, наконец, затронем вопросы устойчивости: возрастает ли ошибка (ограничения, округления или ошибка исходной информации) с ростом х.
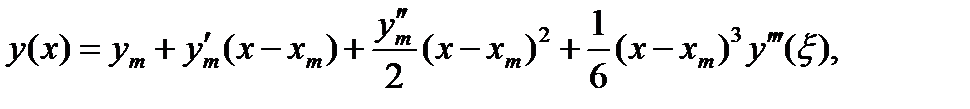
Чтобы определить ошибку ограничения прогноза (6.24), вспомним, что ряд Тейлора для у (х) в окрестности х = хm можно записать в следующем виде:
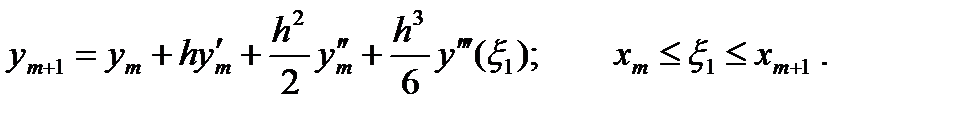
где ξ лежит между х и хm. Полагая x = xm+1, получаем
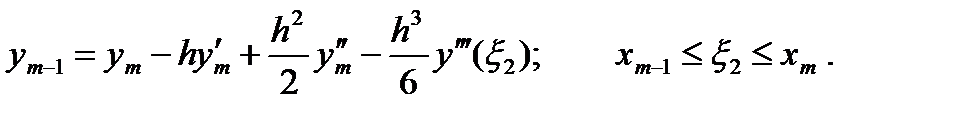
Полагая x = xm-1, находим
Если вычесть одно из другого эти два равенства и заметить, что
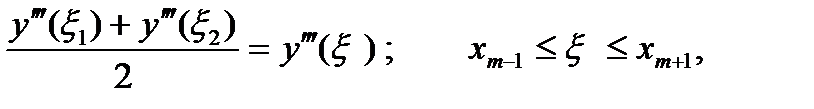
|
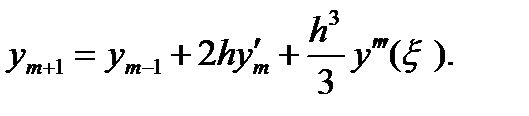
то тогда
Ошибка ограничения, таким образом, равна
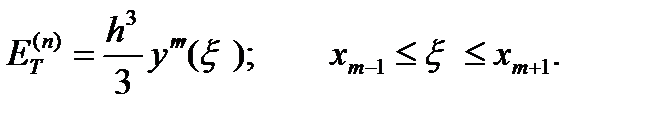
| (6.29) |
Если третья производная практически постоянна, то ошибка ограничения равна Kh3, что и подразумевалось ранее, когда мы говорили, что прогноз (6.24) относится к методам второго порядка.
Мы уже отмечали, что коррекция (6.25) является обобщением формулы трапеций. В предыдущей теме («Численное интегрирование») было найдено выражение для ошибки ограничения формулы трапеций
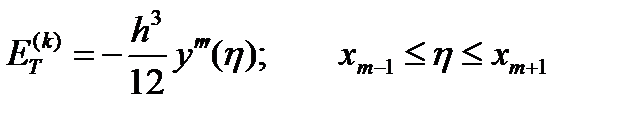
| (6.30) |
Здесь ошибка тоже пропорциональна h 3.
Тот факт, что ошибки ограничения и прогноза и коррекции обе имеют одинаковый порядок, позволяет предложить простой метод оценки 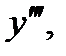 следовательно, и оценки
следовательно, и оценки 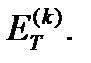
Пусть Ym – точное значение решения при х = хm. Тогда
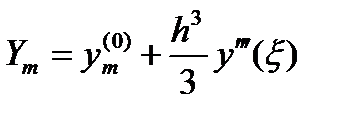

и
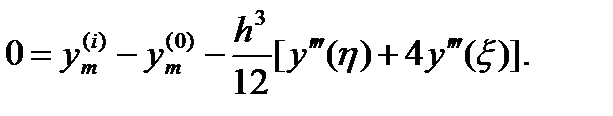
где y (0) m и y ( i ) m вычислены по формулам (6.24) и (6.25).
Вычитая эти равенства одно из другого, получаем
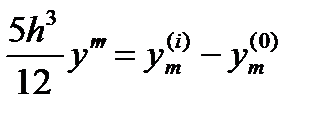
Если предположить, что 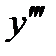 практически постоянна на интервале xm-1 £ x £ xm+1, то
практически постоянна на интервале xm-1 £ x £ xm+1, то
и
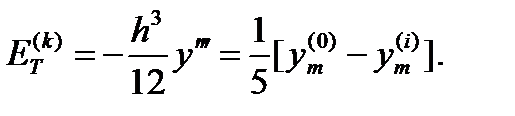
| (6.31) |
Величины, которые требуются для этой оценки, являются просто результатами вычислений по формулам (6.24) и (6.25).
|
|
Таким образом, в противоположность методу Рунге–Кутты метод прогноза и коррекции дает в качестве побочного продукта вычислений легко определяемую оценку ошибки ограничения.
Заметим, что эта оценка получилась такой простой потому, что ошибки ограничения прогноза и коррекции были одного порядка, в данном случае пропорциональны h3. Желательно, поэтому, чтобы любая пара прогноз–коррекция обладала этим свойством.
Рассмотрим теперь вопрос выбора величины шага h.
К сожалению, не существует формул для выбора шага интегрирования до начала решения задачи, за исключением, может быть, формулы (6.27), но, как правило, пользоваться ею довольно неудобно.
Дело в том, что может быть весьма трудно оценить величину М, а если к тому же она сильно меняется на интервале интегрирования, то выбирать величину шага по формуле (6.27) было бы для большей части интервала очень неэкономично, т. к. h получилось бы слишком малым.
Однако, как только вычисления начались, можно оценить ошибку ограничения по формуле (6.31). Если эта ошибка слишком велика, то мы уменьшаем величину шага (часто путем деления пополам).
Если же ошибка гораздо меньше допустимой, то мы увеличиваем величину шага (очень часто это делается путем удвоения).
Можно сделать еще одно замечание по поводу выбора величины шага h.
Из формулы (6.27) следует, что метод сходится, если h < 2/M. Значение М нам неизвестно.
Все же в любом случае очевидно, что чем меньше величина h, тем скорее сойдется итерационный процесс.
Можно поставить вопрос следующим образом: если взять слишком малое h, то на каждую точку потребуется немного итераций, но количество точек будет велико; если же взять большое h, то на каждую точку затратится больше итераций, но само количество точек будет меньше.
Этот вопрос весьма важен, т. к. при прочих равных условиях желательно составить программу так, чтобы затраты машинного времени были минимальными.
|
|
Существуют веские эмпирические соображения, согласно которым оптимальное число итераций равно двум. Под «оптимальностью» здесь понимается минимальный объем вычислений при заданной точности. Другими словами, шаг интегрирования нужно выбирать так, чтобы критерий сходимости (6.26) (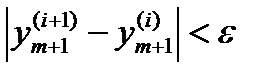 ) выполнялся после двух итераций.
) выполнялся после двух итераций.
Этот критерий легко запрограммировать. Мы подсчитываем количество итераций; если требуется более двух итераций, то мы уменьшаем величину шага; если достаточно одной итерации, то величину шага можно увеличить.
Кратко рассмотрим вопрос устойчивости, т. е. распространения и роста ошибки, возникшей в ходе вычислений.
Не углубляясь в выкладки, можно сказать, что рассмотренный метод обладает относительной устойчивостью в предположении, что fy постоянна.
В большинстве практически интересных случаев это будет не так, но существуют убедительные эмпирические соображения, согласно которым в общем случае относительные ошибки в относительно устойчивых процессах не возрастают. То же самое можно сказать и об абсолютных ошибках в абсолютно устойчивых процессах.
Итак, метод прогноза и коррекции, описываемый формулами (6.24) и (6.25), является относительно устойчивым процессом. Более того, он является абсолютно устойчивым процессом, когда fy < 0.
6.5 Обыкновенные ДУ. Сравнение методов
Мы уже отмечали сравнительные достоинства и недостатки одноступенчатых методов (Рунге–Кутты) и многоступенчатых методов (прогноза и коррекции).
В этом разделе мы дадим сводку характеристик этих методов и предложим способ их сочетания, воспользовавшись достоинствами каждого из них.
Методы Рунге–Кутты
1. Поскольку в методах Рунге–Кутты используется информация только об очередной точке решения и не используется информация о ранее найденных точках, то с помощью этих методов можно начинать решение уравнения (методы являются самостартующими).
2. По той же самой причине, однако, при использовании этих методов приходится многократно вычислять функцию f (x, y) и затрачивать на это много машинного времени.
3. Используя информацию только об очередной точке решения, эти методы позволяют очень легко менять величину шага h.
4. При использовании этих методов весьма трудно получить оценку для ошибки ограничения.
Методы прогноза и коррекции
|
|
Их свойства дополнительны к свойствам методов Рунге–Кутты.
1. В этих методах используется информация о ранее вычисленных точках решения, поэтому с их помощью нельзя начать решение уравнения.
2. Поскольку в этих методах вместо вычисления f (х, у) используется информация о ранее вычисленных точках, то они более экономичны в смысле затрат машинного времени (за исключением, конечно, тех случаев, когда величина шага h слишком велика и требуется много итераций по формуле коррекции).
3. За исключением специальных случаев, не представляющих практического интереса, при любом изменении величины шага h приходится временно возвращаться к методам Рунге–Кутты.
4. В качестве побочного продукта вычислений получается хорошая оценка ошибки ограничения.
Можно предложить следующий путь сочетания двух методов.
1. Начать решение с помощью метода Рунге–Кутты, например, по формуле (6.23) и найти y1.
2. Для вычисления следующих ym использовать прогноз (6.24) и коррекцию (6.25).
3. Если для вычисления очередного значения yi требуется более двух итераций или если ошибка ограничения (см. (6.31)) слишком велика, надо уменьшить величину шага h (см. пункт 4). Если же ошибка ограничения слишком мала, то величину шага можно увеличить.
4. Чтобы изменить величину шага, примем последнее значение уi, которое еще было вычислено достаточно точно, за исходное. Решение уравнения придется снова начать с новой исходной точки методом Рунге–Кутты и только затем снова перейти к методу прогноза и коррекции.
5. В любом случае, когда с помощью формулы коррекции вычислено очередное значение у ( i ) m, окончательное значение ym следует рассчитывать по формуле (6.31).
6.6 ОДУ. Влияние неточности исходной информации
Невозможно в рамках этого курса проанализировать все возможные случаи влияния неточности параметров исходного ДУ или начального условия.
Пример
Дано уравнение 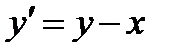 при начальном условии y (0) = 1.
при начальном условии y (0) = 1.
Точное решение имеет вид y = x + 1.
Предположим, что начальное условие задано с точностью 1 %.
Тогда решение будет в пределах от y (1) = 0,01ex + x + 1 до y (2) = –0,01ex + x + 1.
Легко проверить, что при x = 5 ошибка в определении y может достичь 0,01e5, или около 25 %, тогда как ошибка в начальном условии была всего 1 %. Относительная ошибка быстро растет с ростом х.
|
|
Никакой численный метод не даст решения этого уравнения с точностью выше 25 % при х = 5, т. к. ошибка заложена уже в исходной информации.
Это один из примеров неустойчивости решения.
6.7 ОДУ. Представление о конечных разностях
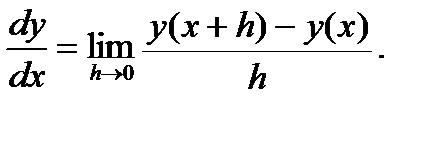
По определению, производная функции одной переменной имеет вид
Компьютер не может совершить предельный переход (да и мы тоже, если функция задана таблично!).
Однако мы можем придать h малое (но не нулевое) значение и проверить, получается ли приближение достаточно точным (проблема точности) и не возрастает ли ошибка в ходе вычислений (проблема устойчивости).
Метод сводится к тому, что производная заменяется разностью.
Разность y (x + h) – y (x) называется конечной разностью.
Пример для многочлена y (x) = 8x3 – 2x + 1 приведен в табл. 6.1.
Таблица 6.1 – Таблица разностей для многочлена y (x) = 8x3 – 2x + 1

Разности первого порядка:
Dy (0) = y (0,5) – y (0) ,
Dy (0,5) = y (1) – y (0,5) ,
Dy (1) = y (1,5) – y (1) и т. д.
Если первые разности разделить на величину шага (здесь 0,5), получим грубую оценку производной (тангенса угла наклона касательной) в разных точках.
В общем случае, когда шаг равен h, правая разность первого порядка функции y (x) в точке x = a имеет вид
Dy (a) = y (a + h) – y (a).
В более привычной записи конечная разность функции y (x) в точке xi:
Dy (xi ) = y (xi+1 ) – y (xi ) = yi+1 – yi.
В исчислении разностей рассматриваются и разности второго порядка в точке xi:
D2y (xi ) = D (D y (xi )) = (y (xi+2 ) – y (xi+1 )) – (y (xi+1 ) – y (xi )) =
= y (xi+2 ) – 2 y (xi+1 ) + y (xi ) = yi+2 – 2yi+1 + yi.
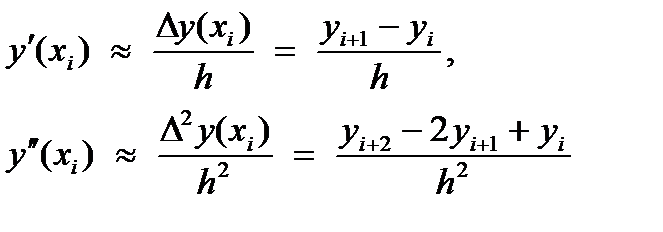
Т. о., приближенно можем записать
Более подробно метод сеток будет рассмотрен в следующей теме.
6.8 ОДУ. Краевые задачи – введение
До сих пор рассматривались задачи с начальными условиями. Часто бывают даны условия на решение в двух точках.
Иллюстрация приведена на рис. 6.7. Краевые условия имеют вид y (a) = A, y (b) = B.
| Рис. 6.7. Геометрическая иллюстрация краевой задачи |
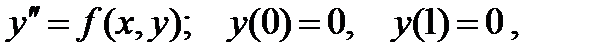
Например, может быть дано уравнение
и требуется узнать у = у (х) для 0 £ x £ 1.
Эта ситуация может быть сведена к предыдущему случаю (т. е. к задаче с начальными условиями) методом проб и ошибок.

Начнем с уравнения
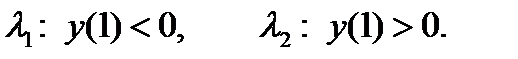
и попробуем найти два таких значения l1 и l2, чтобы выполнялись следующие соотношения:
Так как для большинства практических задач y (1) есть непрерывная функция l, то можно, даже используя грубый метод деления отрезка пополам, за 10 проб уменьшить длину отрезка | l1 – l2 | в 210, т. е. более чем в 1000 раз.
Однако вместо того чтобы сводить краевую задачу к задаче с заданными начальными условиями, нередко выгоднее решать ее непосредственно. На этот счет имеется обширная теория, и мы кратко рассмотрим лишь один пример, чтобы показать некоторые из содержащихся в ней идей.
|
|
Рассмотрим уравнение
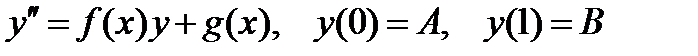
| (6.32) |
Прежде всего, аппроксимируем у" второй разностью
 , ,
| (6.33) |
считая, что интервал 0 £ x £ 1 разделен на N интервалов величиной h = 1/N.
Таким образом,
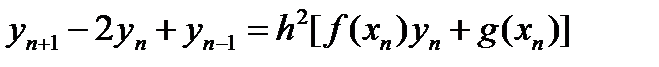
| (6.34a) |
или
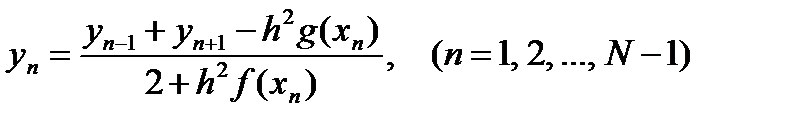
| (6.34b) |
Получили N – 1 линейных уравнений с N – 1 неизвестными, которые могут быть решены многими различными способами.
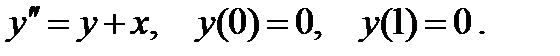
В качестве примера рассмотрим один частный случай уравнения (6.32).
Положим A = B = 0, f (x) = 1, g (x) = x и N = 4, т. е. уравнение
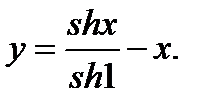
Решение известно:
Разностные уравнения имеют вид (см. (6.34а))
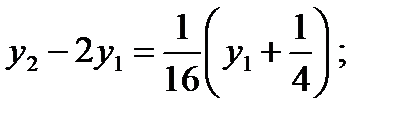
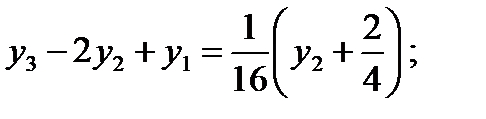
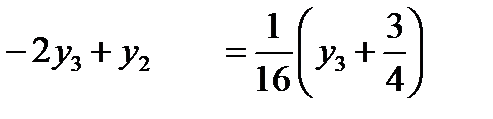
или

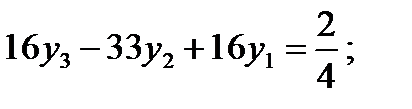
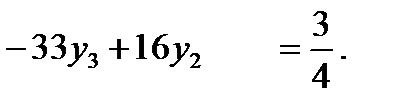
Умножим первое из уравнений на 16, второе на 33 и третье на 16 и сложим. Получим
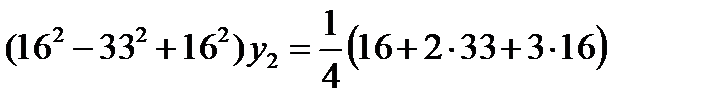
Зная y2, легко найти у1 и у3 из первого и третьего уравнений.
Что можно сделать для уточнения решения? Можно положить N = 8 и, используя вычисленное решение для N = 4, оценить решения для N = 8. Затем, подставляя это решение в правые части восьми уравнений, можно вычислить улучшенные значения и повторять процесс до тех пор, пока не прекратятся изменения.
Число точек можно увеличивать как угодно.
Постановка краевых задач
Пусть дано дифференциальное уравнение второго порядка:
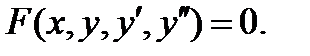
| (6.35) |
Двухточечная краевая задача для уравнения (6.35) ставится следующим образом: найти функцию y = y (x), которая внутри отрезка [ a,b ] удовлетворяет уравнению (6.35), а на концах отрезка – краевымусловиям
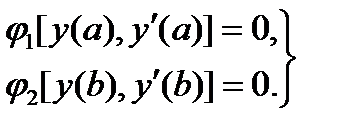
| (6.36) |
Краевая задача называется линейной краевой задачей, если уравнение (6.35) и граничные условия (6.36) линейны. При этом дифференциальное уравнение и краевые условия записываются в виде

| (6.37) |
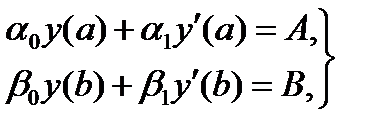
| (6.38) |
где p (x), q (x), f (x) – известные непрерывные на отрезке [ a, b ] функции, a 0, a 1, b 0, b 1, A, B – заданные константы, причем
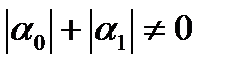 и и 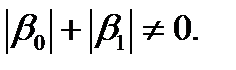
|
Если A = B = 0, краевые условия (6.38) называют однородными.
Методы приближенного решения краевых задач можно разбить на две группы: разностные и аналитические методы.
|
|
|

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!