

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...
Топ:
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Найдем формулы вычисления векторного произведения векторов, если векторы заданы координатами:
 ;
;
 .
.
По свойствам векторного произведения
 =
=
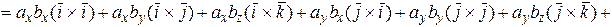
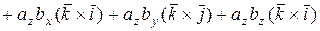 . (2)
. (2)
По свойству 1 векторного произведения

 ,
,  ,
,  .
.
Векторы  образуют правую тройку, круговая перестановка векторов (рис. 3) ориентации не меняет, поэтому
образуют правую тройку, круговая перестановка векторов (рис. 3) ориентации не меняет, поэтому
 ,
,  ,
, 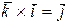 .
.
Перестановка соседних векторов меняет ориентацию (рис. 10), поэтому
 ,
,  ,
,  .
.
Подставим векторные произведения базисных векторов в равенство (2), получим

 .
.
Последнее равенство есть не что иное, как разложение определителя по первой строке

 .
.
Поэтому
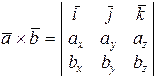 (3)
(3)
– формула вычисления векторного произведения в координатах.
Найдем формулу вычисления в координатах площади параллелограмма, построенного на векторах  и
и 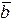 (рис. 5). По формуле (1)
(рис. 5). По формуле (1)

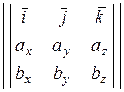 ,
,
т. е. площадь параллелограмма, построенного на векторах  и
и  , равна модулю определителя, первая строка которого – базисные вектора, а вторая и третья – координаты векторов
, равна модулю определителя, первая строка которого – базисные вектора, а вторая и третья – координаты векторов  и
и  .
.
Если векторы лежат на плоскости  , т.е.
, т.е.  ,
, 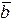
 ,
,
 ;
;  ,
,
то площадь параллелограмма, построенного на векторах  и
и 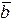 равна
равна
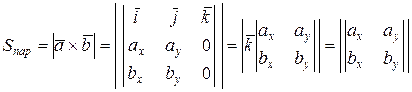 .
.
Геометрический смысл определителя второго порядка: его модуль равен площади параллелограмма, построенного на векторах, координаты которых расположены в строках определителя.
Пример 1. Даны точки  ,
, 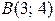 ,
,  . Найти площадь треугольника АВС.
. Найти площадь треугольника АВС.
 Рис. 11.
Рис. 11.
|
Решение. Площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах  и
и  (рис. 11). Найдем векторы
(рис. 11). Найдем векторы
 ,
, 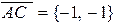 .
.
Тогда из геометрического смысла определителя второго порядка площадь параллелограмма

 .
.
Ответ: 
3. Смешанное произведение векторов, его свойства. Признак компланарности векторов. Смешанное произведение в координатах.
Определение 2. Смешанным произведением трех векторов  ,
, 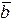 и
и  называется число
называется число  , равное скалярному произведению вектора
, равное скалярному произведению вектора  на векторное произведение векторов
на векторное произведение векторов 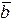 и
и  , то есть
, то есть
|
|

 .
.
Найдем геометрический смысл модуля смешанного произведения. Объем параллелепипеда, построенный на векторах  (из рис. 12)
(из рис. 12)
 ,
,  ,
,
 ,
,  .
.
При этом знак « » необходим, чтобы длина высоты была положительной. Тогда
» необходим, чтобы длина высоты была положительной. Тогда

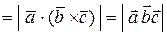 .
.
Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах, как на сторонах.
Найдем формулы для вычисления смешанного произведения векторов, если векторы заданы координатами:
 ,
, 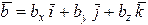 ,
, 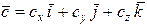 .
.
Тогда
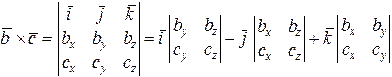 .
.
Скалярное произведение вектора  на векторное произведение
на векторное произведение 
 .
.

– формула вычисления смешанного произведения в координатах.
Учитывая формулу для вычисления смешанного произведения в координатах, получаем геометрический смысл определителя третьего порядка:
 , (4)
, (4)
модуль определителя равен объему параллелепипеда, построенного на векторах, координаты которых расположены в строках определителя.
|
|
|

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!